This content originally appeared on Level Up Coding - Medium and was authored by Robert Hirsch
How can we predict outputs of systems with random inputs?
If you haven’t heard the word “stochastic” before you are in the majority and can be utterly forgiven. But the amazing thing is that almost every aspect of life is driven via stochastic processes. Let’s take a look at what it is and how it relates to blockchain.
All stochastic means is that something behaves in a random way. More importantly, stochastic systems have statistically predictable range of outputs based on a random set of inputs (which may, themselves be random, but still not evenly spread out, more on that later).
A quick gander at wikipedia gives a remarkable list of economic, scientific, and social segments that are driven by, and can be modeled as, stochastic processes. But let’s try an easy example to try to wrap out heads around stochastics.
Flipping the coin

Ok, it’s hard not to start here when discussing randomness and stochastics. Randomness decides the result of each individual coin flip. Stochasticity describes a set of outcomes based on the random input. So, for example, in this case, we will say, “For 1000 coin flips, 50% of the, will be heads and 50% will be tails”. The outcome of an individual coin flip is random, the 50:50 outcome of many flips is the stochasticity.
I know, it’s not a brain exploding revelation, let’s keep going and see how we can use this.
Plinko

Plinko and its cousin the Galton Board, show stochasticity in action. In the video above you can see that each marble has some set of random initial conditions before entering the board (initial position, speed upon entry, rotation after hitting other beads, etc) and this will move in a random directions when hitting a peg. It doesnt matter how many times you flip the Galton board up, the end result will be the beads in that same distribution: very few beads at the ends, and a larger amount of beads at the middle. This is called a normal distribution, it will happen every time.
Randomness are the conditions upon which the marble enters the board adn travels down it. Stochastics is the resulting normal distribution that the balls end up in.
If you want to deep dive further, programmatically, into this topic, here is a great resource about programming a plinko board. And here is an applicaton of plinko programming to simulate gambling outcomes, so simulating plinko, believe it or not, has real world use!
Monte Carlo Simulation
When we program simulations of stochastic systems, we can do this by performing what is called a Monte Carlo simulation. First, you programatically set up the inputs, and the system in software, such that you can see the outcome of one single trial. So for plinko, you could simply make a random choice of “left” or “right” each time a ball hits a peg, or you can set up a physics model, and ramdomize the initial conditions of a ball. Either way, you can simulate the path of each ball as it goes down the plinko board.
With that model in hand, you run it thousands of times to see the distribution of outputs. In the case of Plinko, it’s a normal distribution.
There is an excellent piece of software called Crystal Ball, for Microsoft Excel, that lets you perform multi-input, multi-output stochastic analysis via Monte Carlo simulation. Its used in every industry because the answer to “What is this value?” is usually a range of numbers, and often in a normal distribution. Thus the outputs of the models are also a range of numbers. If you can determine the range of the output numbers, then you can predict, for example, how many bad parts you will get from a process where inputs have randomly distributed ranges.
Weighted inputs
One more topic before we get to see this in action in blockchain. Its important to understand, that inputs can be weights also. For example, these three curves, which may describe the diameter of a piston from three different manufacturers.
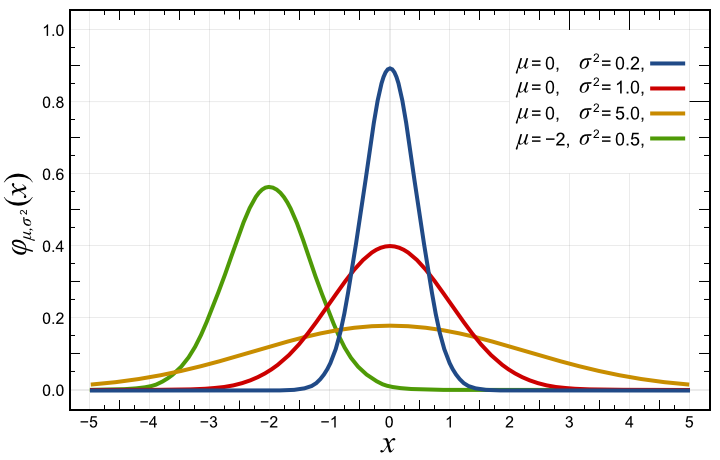
If we take the red distribution of piston diameters as our current vendor, we can examine the distribution of the parts from other vendors. Green vendor supplied parts that are almost always too small. So we would reject that vendor. But Blue vendor not only supplied parts with the same target as we currently use, but there are fewer away from the target dimension. We should switch vendors!
But wait! Maybe not! An engine is a complicated thing, maybe the importance of this dimension is not as high as other parts. Maybe the range of output energy of a spark plug is more important, maybe the range of air intake is more important (obviously I don’t know jack about engines), these things are linked together to product the output torque. So we might multiply these inputs by a weight to raise or lower their affect on the whole system.
Stochastics in Blockchain

Let’s take some time to apply this in blockchain. The verification process, the block linking process, the wallet creation process, and more are all created via the incorporation of randomness. The security is utterly reliant on the randomness of extremely large numbers.
Parts of blockchain, the stochastic parts, are perfectly predictable, which is great! Let’s take a look at one. Bitcoin is boring, let’s look at an up and coming blockchain project, Divi!
Divi is descended from Bitcoin, Dash and PIVX, and has economic mechanics like many other similarly descended chains (for example, Phore, Rapids, and Particl). The economy has two parts, the masternode network, and the staking nodes. There are some knowns about the economy:
- The average block time is about a minute, which means that there are about 10080 blocks in a week
- The number of masternodes are always known, and how many of each tier are also always known.
- The number of coins held in masternodes is always known, and the total number of coins are always known
There are other important aspects that can be derived from the blockchain, but these are all we really need. Someone in the community (me, but derived from work of other community members) made a tool to look at the ecosystem from a 10,000 foot view.
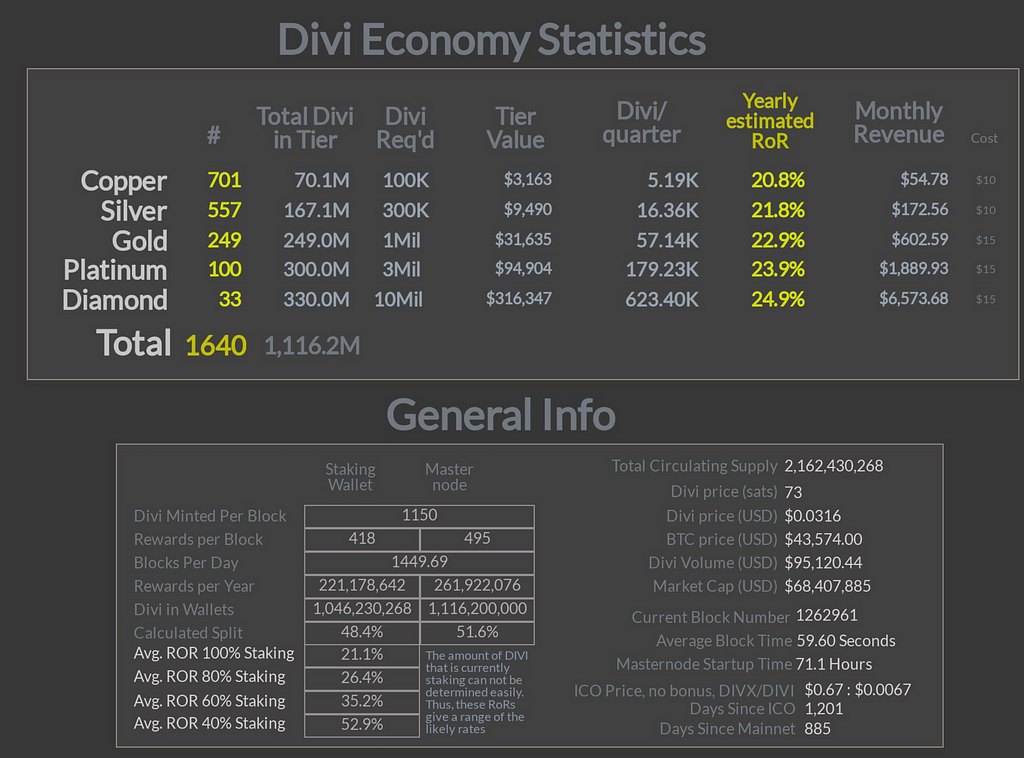
There is a lot of information there, but it’s used to communicate the answer “How are we doing?”. But if blockchain and Divi run on random processes how can we be sure that a copper masternode will get 5190 Divi every quarter? The answer is: We can’t, because the ecosystem is stochastic. Not only is it stochastic, but it is alive, in that these numbers are constantly changing, it’s just a snapshot. If you go to the website for this tool, you will find a slightly different answer.
Further, while this image shows the average results across the Divi economy, its doesn’t tell you anything at all about your specific wallet, or how much income you will get this week. Your wallet is just one of thousands of columns at the bottom of a Plinko board, your copper is out the the side, you diamond is closer to the center. No one call tell you how it will do this minute, this week, or even this month with precision, but we can perform a monte carlo simulation on all the wallets, and see what sort of ranges we are looking at.
Setting up a Divi masternode Monte Carlo simulation
To do this, we need to set up the plinko board, but for the Divi ecosystem. We know that every single block, a masternode gets rewarded. We also know that the masternodes are weighted. From their white paper:
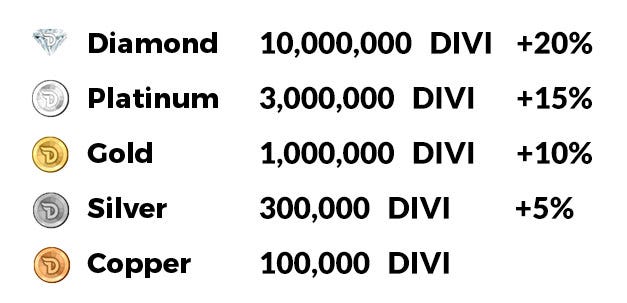
What they are saying here is that moving up the tiers improves your income beyond just the increased amount of Divi that you hold (a staking node does not have this advantage, your weight in the ecosystem is determined solely by the amount of coins you have).
So lets say a copper masternode has a weight of 100 (because I like to stay away from float numbers when programming if I can). The weight of a silver will be 300 (because it has 3 times as many coins) plus a bonus of 5%, so the silver weight is 315. So we get weights as follows:
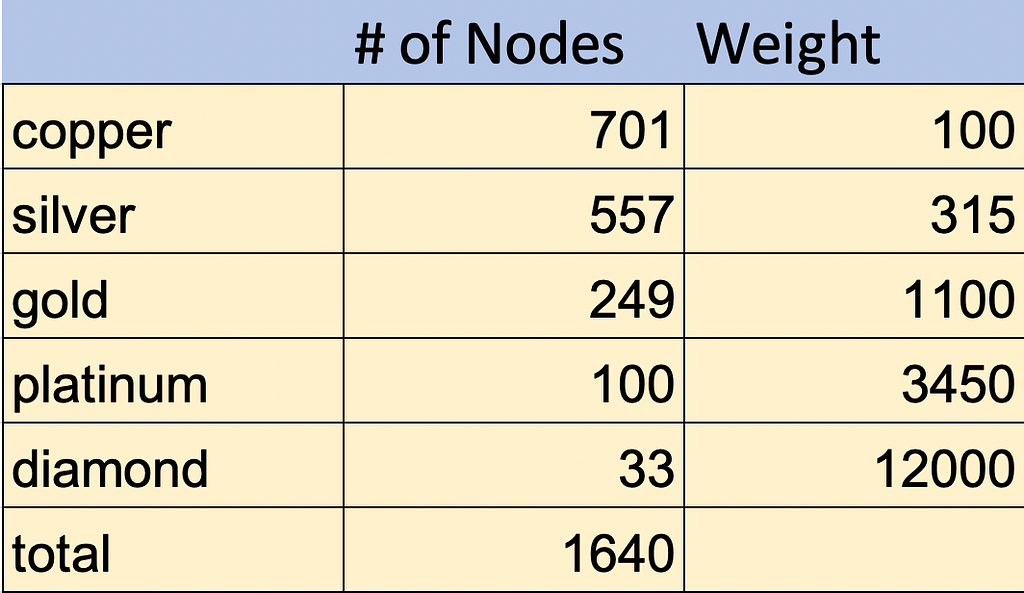
How do we use this information so that we can perform the monte carlo? Well we want to find a total weight of the system, the individual node weights and the number of nodes.
Wt=sum((# of nodes in tier)*(tier weight))
Wt = (701*100) + (557*315) + (249*1100) + (100*3450) + (33*12000)
Wt=1,260,455
From this we can determine the chance that any tier will get a reward, and then the chance that any node will get one.
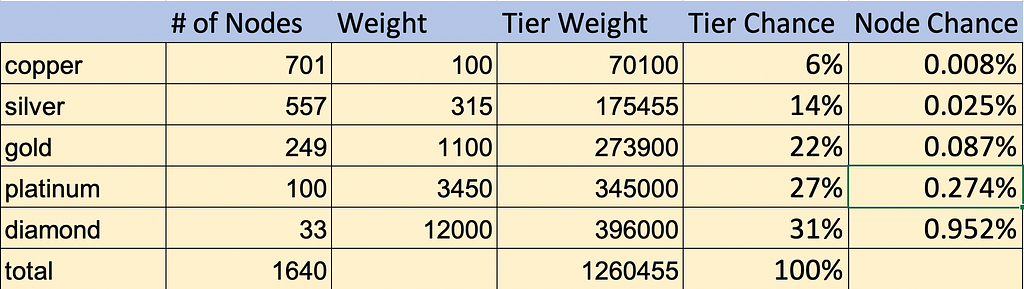
So, using the very right column, you can figure out your AVERAGE income from a tier. But you can not determine when, or what the range of rewards you might get in a week. for that, we need to move to monte carlo.
We can think of the Tier chance as an area. If we create a system where we shoot a randomly aimed arrow at a target and assure that the target is hit, then the Tier chance will represent the areas of each band on the target.
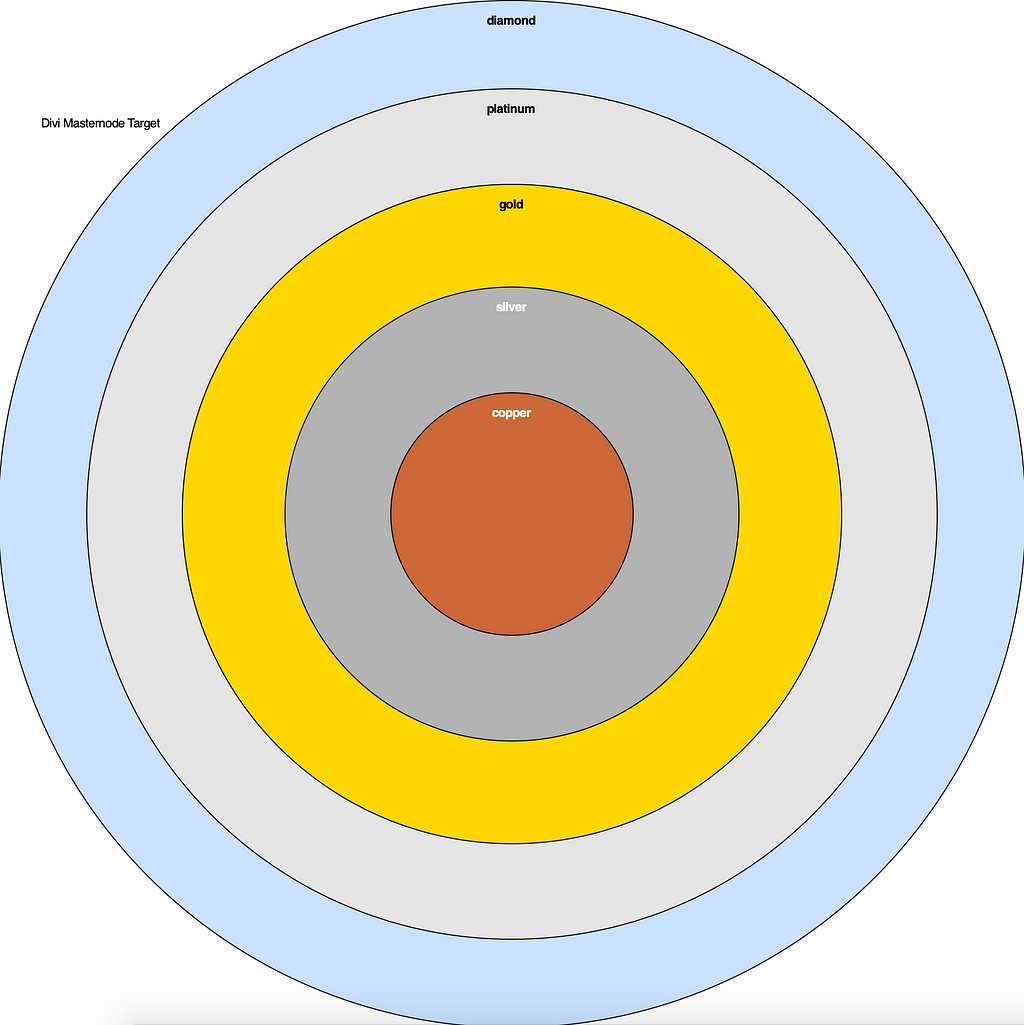
I am aware that the areas seem equal in this image, but the area in the Diamond region is 5.65 times larger than the area in the Copper region. You can build this yourself as the code is available on github.
So, lets put the masternodes on there, and start the simultion. If we break up each tier into its nodes, we will see this:
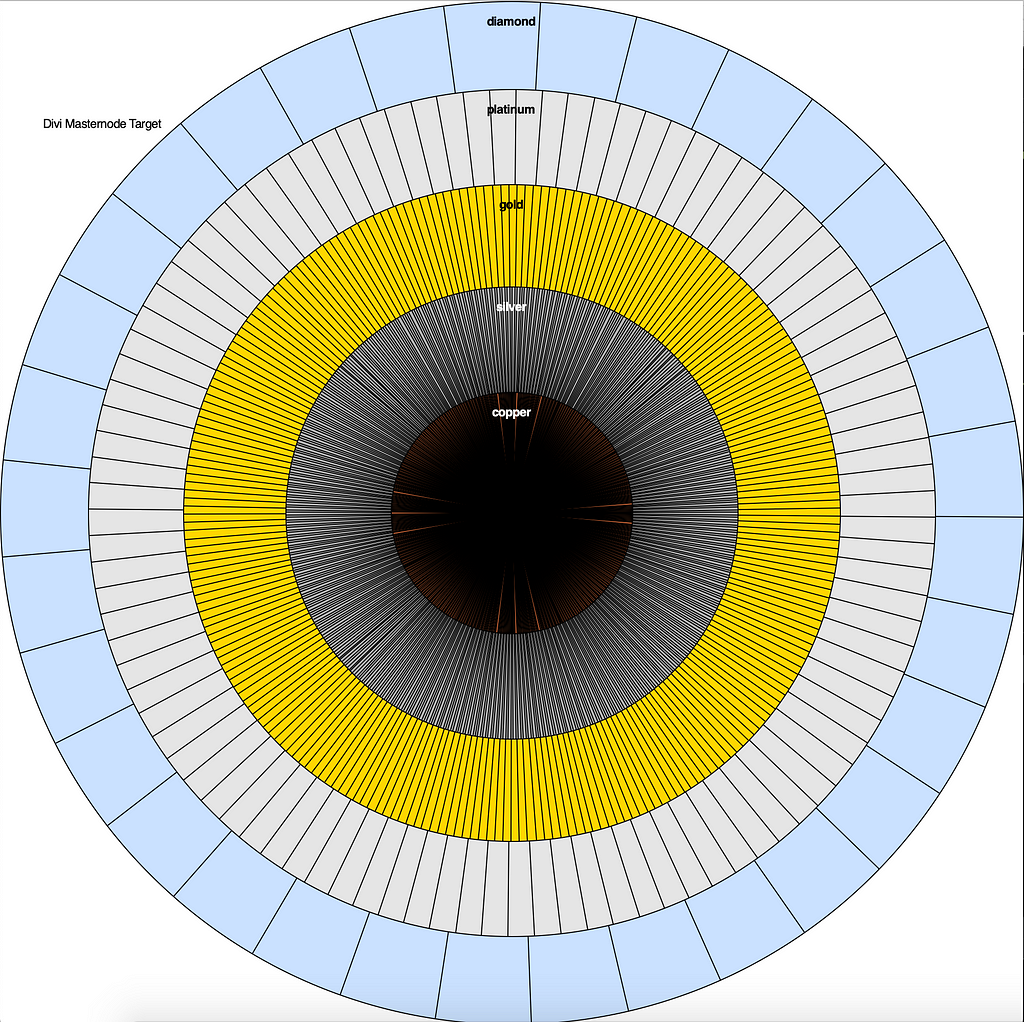
Here, the chances of your node getting a reward can be seen better. If you have a diamond, you have a large amount of space on the largest area of the target. If you have a copper, you have the slimmest sliver of space on the smallest area of the target.
OK, let’s throw 10080 darts at this target, representing a week of rewards, randomly giving rewards to all the masternodes.
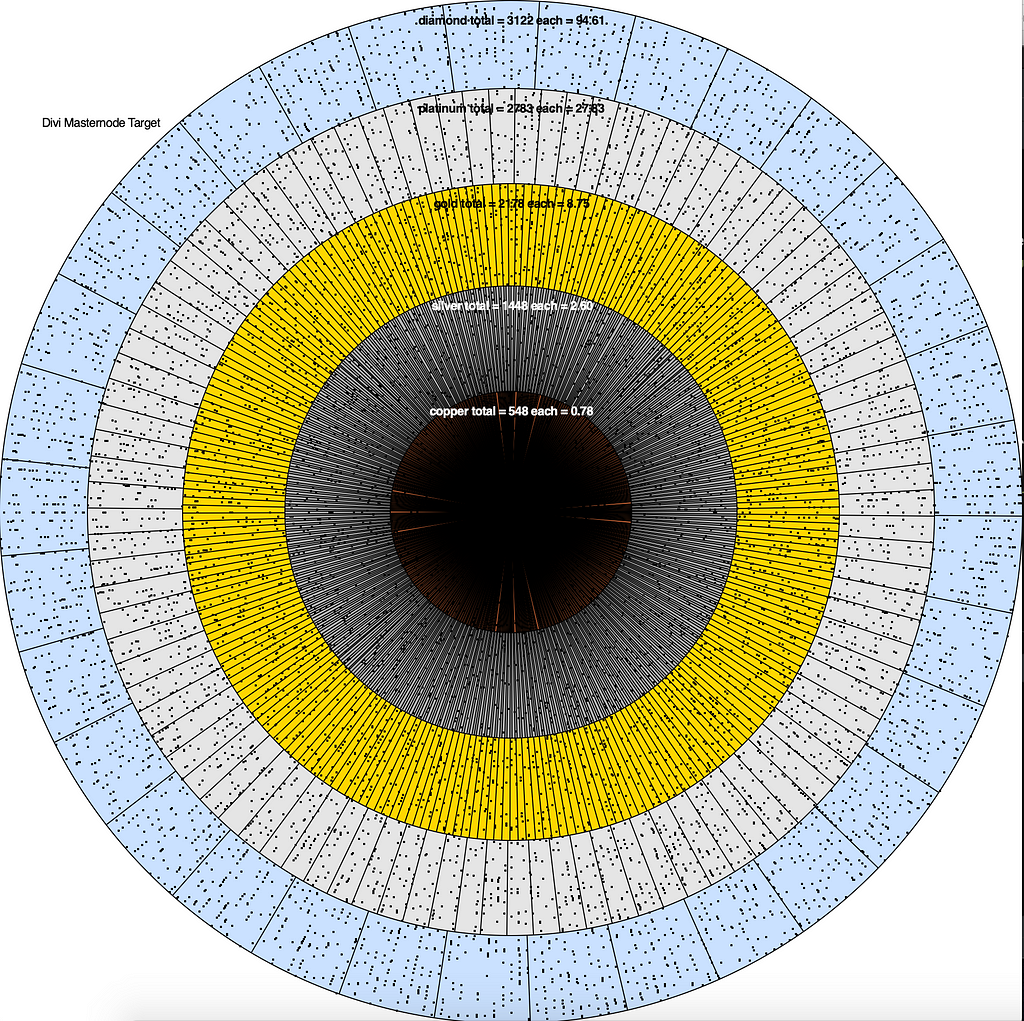
You can see that if you have a Divi Diamond masternode you can expect, on average, 94 rewards (of 495 Divi each) every week. But you can see that some diamonds get skimpy rewards, while others get loaded up.
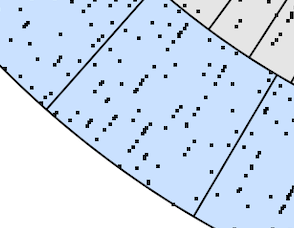
The lower diamond node received only 76 rewards this simulated week, while the upper diamond node received 91. I didnt check them all, but obviously still others got over 100.
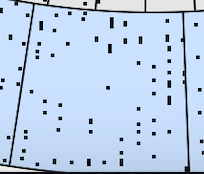
What about the coppers? Lets zoom in.

Each little sliver represents a single copper node. You can see, that for the entire week between the pie slice of yellow lines there are 10 coppers that didnt get a single reward this simulated week, and there are many more. While, if you look at the other highlighted copper, it received 5 rewards this week. If I run the sim again, and look at that exact copper segment, I will likely find that it did not receive any rewards, but because this is all random, it’s totally possible to receive another 5 rewards in the next simulated week.
When rewards?
I hope this article has shed some light of stochastic systems. If you are invested in the Divi project and are asking “Is it normal for my copper to not receeive a reward for 3 weeks?” Then I hope this has help ed you understand that both a tersity of rewards and a deluge of rewards are totally normal and expected. If you have a higher tier node, then you can expect rewards every day, and its much easier to know if something is wrong or not. The lower tiers need to wait at least a month, maybe even 90 days to know if everything is normal. [sidenote: your masternode reports to you if things are normal or not, having one doesn’t preclude you from checking on its health once in a while].
If you are interested in the staking node side of the Divi ecosystem, I have previously written something on that too.
Stochastics: A Primer was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Robert Hirsch
Robert Hirsch | Sciencx (2021-03-31T03:17:56+00:00) Stochastics: A Primer. Retrieved from https://www.scien.cx/2021/03/31/stochastics-a-primer/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
