This content originally appeared on Level Up Coding - Medium and was authored by Tanishq Vyas
A comprehensive introduction to Segment Tree

1. What is a Segment Tree?
Let’s say we have an array A of size N. A segment of the array is a contiguous part of an array in form A[i : j] such that 0 ≤ i ≤ j ≤ N-1.
A segment tree is essentially a binary tree in whose nodes we store the information about the segments of a linear data structure such as an array. Do not worry about what kind of information as of now. We shall take a look at that in the later sections of this article.
- The root node of the segment tree would contain the information about segment A[0 : N-1]
- The left child of the root node would contain the information about segment A[0 : (N-1)/2] and similarly,
- The right child of the root node would contain the information about segment A[ 1+((N-1)/2) : (N-1) ] and so on.
In simpler terms the root node contains information about the whole array, its left child contains a similar kind of information about the left half of the array, and the right child of the root node will contain the information about the right half of the array and so on. Thus at each step (level of the tree), we divide the segment into two halves and the further children nodes contain the information about these two halves.
This continues till we reach the leaf nodes which contain the element of the array A itself. The i-th leaf node contains A[i]. Thus we can say that there will be N leaf nodes and the height of the tree will be log N to the base 2.
Note: Once a segment tree is built for an array, its structure cannot be changed. We are allowed to update the values of the nodes but we cannot change the structure of the Segment Tree. That is to say, we cannot add more elements to the array and expect the segment tree to update. In that case, we will have to create a new segment tree altogether. However, we are allowed to update the values of the array and the segment tree shall be updated accordingly.
Segment Trees allow for the following two operations:
- Update : This operation allows us to update the values of array A and reflect the corresponding changes in the segment tree.
- Query : This operation allows us to perform a range query on the array. For example, let's say we have an array of size 15 and we wish to find the maximum element in the segment of an array with start index as 3 and end index 9. This is an example of a range query.
Thus we can say that a segment tree comes in handy when we have a lot of range-based queries to be performed on an array along with value updates on the same array. The process of creation of a segment tree takes some time but once it's done, the operation of range queries becomes very fast.
2. What kind of information does a segment tree hold?
Now that we have a basic understanding of the structure of the segment tree let us have a look at what kind of information does a segment tree hold.
Consider an array A = [1, 4, 5, 8, 0, 13]
Now a segment tree is always associated with a piece of certain information that is directly linked with the kind of range queries we wish to perform. A couple of them are as follows:
- Find the sum/product of elements of an array in the range A[i : j]
- Find the maximum/minimum element in the range A[i : j]
- Find the count of even/odd/prime etc, numbers in the range A[i : j]
there can be many others depending upon the usage. Let us have a look at how we can make use of a segment tree to find the sum of elements in a given range.
3. Creation of Segment Tree
Let’s say we have an array A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] and we wish to find the sum of elements in a given range. Then each node would store the sum of its children nodes, except the leaf nodes which store the array elements.
Then the segment tree for the same would look something like this
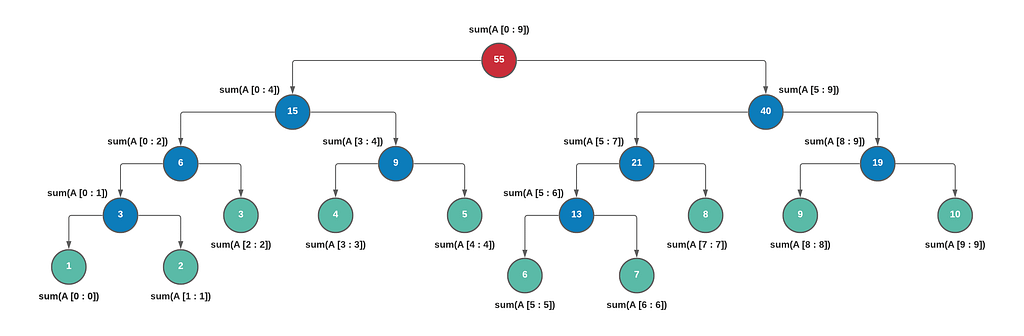
The red node being the root node, the blue nodes being the internal nodes and the green nodes being the leaf nodes. Each node contains information about a particular segment of the array. In this example,
- Root node contains the sum of all the elements of the array
- The left child of the root node contains the information about the sum of the left half of the array i.e. [1, 2, 3, 4, 5]. Its left child in turn contains the sum of the segment [1, 2, 3] and the right child contains the sum of the segment [4, 5] and so on.
- The right child of the root node contains the information about the sum of the left half of the array i.e. [6, 7, 8, 9, 10]. Its left child in turn contains the sum of the segment [6, 7, 8] and the right child contains the sum of the segment [9, 10] and so on.
If we wanted to compute, let's say, the maximum element then we would be storing the maximum element in each segment in the corresponding nodes. Thus before building the Segment Tree one must figure out the intent behind building the tree and the type of values to be stored in the tree’s nodes.
Thus we can also notice that a segment tree is always going to be a full binary tree i.e. each node either has 2 or 0 children.
References
Segment Tree was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Tanishq Vyas
Tanishq Vyas | Sciencx (2021-05-04T11:46:29+00:00) Segment Tree. Retrieved from https://www.scien.cx/2021/05/04/segment-tree/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
