This content originally appeared on DEV Community and was authored by thunderbiscuit
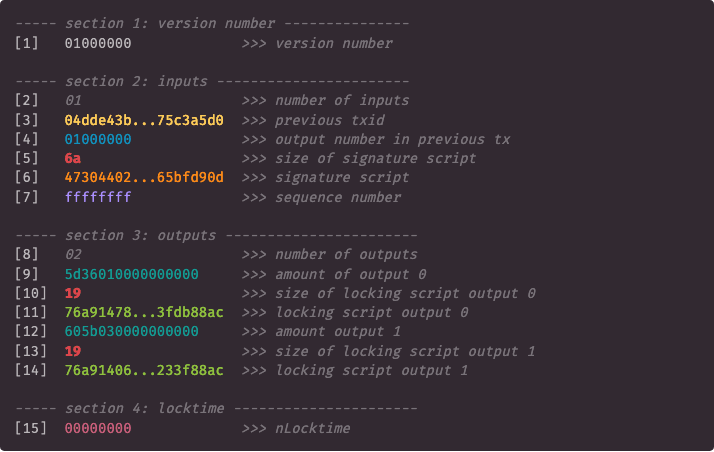
Here is a hex dump of the raw bitcoin transaction e778e8765fdbb60f62e267de4705789f526a5fe9bb0c0f5e56ab4f566c5240eb:
You've seen bitcoin transactions expressed in this form if you've ever tried to dive into the more technical bitcoin books, or have just been lurking around in the bitcoin community for long enough. They seem arcane and of impenetrable complexity, but it turns out that that's not the case at all; the above transaction, for example, is composed of 15 small building blocks, each one easy to find and interpret.
Studying the structure of bitcoin transactions in their "true" form is a valuable quest for all bitcoiners. This article is written with the curious bitcoiner in mind looking to get a high level understanding of what exactly gets passed around from node to node on the network. Let's get to it.
Priors
To really understand all pieces of a transaction, a basic grasp of 4 foundational, non-bitcoin concepts are important: bytes and hexadecimal notation, endianness, variable-length fields, and varints. I address all 4 of those in the sections below, but if you are familiar with computer science in general you most definitely won't need this kind of entry level review. If you are not familiar with them, however, I think you'll find them enlightening, and they will most definitely serve you well on your journey into bitcoin.
1. Bytes and Hexes
You might have seen "raw" bitcoin transactions printed in hexadecimal format (the transaction above is an example of that). But of course computers only speak the language of bits (0s and 1s). A bitcoin transaction in it's computer-understandable form is therefore a string of binary digits. Moreover, those 0s and 1s are always kept in small groups of 8 bits, called bytes. Here is an example of a byte: 1101 0110.
The problem with binary code is that it's not easy for humans to parse. The transaction above (and it's not even a big one) written in binary format is exactly 1,800 digits (10101011100101000101100000110100000011101...).
But binary numbers are still numbers; if we write them for humans we can write them in any we want that works best. Decimal notation (our regular number system), Roman numerals, Korean characters. etc.
Decimal notation would be an obvious candidate, but it turns out that it is not very convenient for working with bytes. Take for example the bytes 1101 0110 and 0000 0010. In decimal notation, the first number is 214, whereas the second number is 3. In fact every byte, when written in decimal notation, will take between 1 and 3 digits. That's not convenient, because then you'd never know when a byte ends and when the next one starts—how many bytes is 21431042? There can be multiple interpretations.
Instead, a preferred numbering system for writing bytes for human consumption is the hexadecimal number notation. A full explanation is beyond the scope of this post, but you should know that the number of possible arrangements of 4 bits is 16, and that the hexadecimal notation system has exactly... 16 digits. They map out nice and tidy with half a byte.

Notice that we can now represent our bytes as two hexadecimal digits, for a clean notation. Each byte is two hexadecimal digits, like so:
When you're looking at a big hexadecimal string like the one at the beginning of this post, you're really just looking at a neat little representation of a bunch of bytes, with each block of two characters representing one byte.
2. Big-Endian and Little-Endian Ordering
Endianness refers to the order of bytes within a representation of a number. You can think of it as the "direction" in which bytes should be read for meaning, while understanding that either direction does not influence the ultimate meaning of the bytes.
Take for example the number one thousand five hundred and ninety two. You are probably used to reading a number like this in the following way: 1592. At the same time, if I told you that I had this weird habit of always writing my numbers from right to left, you would still know that 2951 means one thousand five hundred and ninety two, because you'd know me and understand my weird habit.
It turns out that some computer architectures are more efficient when working with numbers if they are stored with the least significant byte first (the equivalent of reading right to left), and so a lot of the numbers we use when communicating with computers are "translated" to that format. We call this computer version of a number little-endian, because it starts with the little end. When shifting from big-endian to little-endian, it's the bytes that we shift. This means shifting the last two characters (remember that one byte equals two hexadecimal characters) for the two up front, and so on.
The number 220,000 in hexadecimal notation is written 03 5b 60, but expressed in little-endian it becomes 60 5b 03.
A real life example would be our transaction id for this article, which if referred to within a bitcoin transaction will be written in its little-endian form, but if you try to look it up in a block explorer, you'll need it's "human", big-endian version:

3. Variable-Length Fields
You'll notice that the bytes in a transaction are all glued together in one big continuous blob. How does the software know where an input start and where it ends? How does it know if a certain byte belongs to the number of bitcoin transmitted or to the receiving address? The flexibility offered by bitcoin transactions implies that there are an extremely rich number of combinations possible, and that the scripts required for unlocking utxos vary greatly in length.
One way to deal with this uncertainty would be to give every field a set length in bytes. This is what the version field does, for example: the version number of a transaction is always written in the first 4 bytes of a transaction (see the 01000000 number that starts the transaction below). In a lot of cases, however the length needed to transmit the necessary data differs widely between transactions: unlocking scripts for a simple Pay to Public Key hash might be 106 bytes long like in the transaction we are using in this post, but they can easily be 5 times that size on complex multisig scripts. Giving a fixed length to that data section would not only be inefficient (a lot of transactions would not need that much space at all), it would also be limiting, because scripts would have to stay under that size.
A better way to deal with this and keep both flexibility and efficiency is by using a small marker at the beginning of a variable-length section that will give the software an indication of the lenght of the section to follow. Here is an example of a series of 6 bytes: 05 e7 78 e8 76 5a. If we knew that the first byte was a indicator byte for the length of the section, a plain-english reading of this would then look like this:
byte 1: 05 >>> the following section is 5 bytes long
bytes 2 to 6: e7 78 e8 76 5a >>> data
Bitcoin transactions use a mix of fixed-length fields and variable-length fields. I'll make note of which ones use which in the description of each parts.
4. Varints
Variable Integers (varints) are a way to write a very wide range of numbers in a way that minimizes their cost on transaction space.
To understand how they accomplish this, first note that the bigger the number we need to write down, the more bytes it requires. Three is written as 00000010 (1 byte), whereas two million twenty nine thousand five hundred and twelve is written as 000111101111011111001000 (3 bytes).
The problem we are faced with is that all bytes are glued together in one long string of 0s and 1s, and the software needs to know exactly where each of the fields pertinent to a transaction start and end. One way to deal with this is to give fields a never-changing length, so that we always know when they end. This is what the version field does, for example: the version number of a transaction is always written in the first 4 bytes of a transaction (see the <code 01000000 number that starts the transaction below). The problem with this approach is that if we sometimes need to accommodate numbers of great size, we will need to give the field a length with the ability to accommodate all of those numbers (say 8 bytes dedicated to a particular field). But if in most cases we only use the field for very small numbers, then a lot of those bytes are just wasted, because those small numbers only need 1 byte. If this type of field is required in multiple places in a transaction, all that waste starts to add up. Rather, we need a solution that will use only the space required for the number we wish to write. This is what varints do; they use 1 byte for most of our use cases, and up to 9 bytes for the really big numbers we don't expect often.
The way this is achieved is simple. A single byte can normally be used to represent the numbers 0 to 255. If the number we need represented (say, the number of inputs in a transaction) is below 253, we write it in the first byte, and the software knows that that's all there is to it. If the number is big enough that it needs a few more bytes to write, we instead write 253 in that first byte, which will be interpreted by the software as "read the next two bytes as the actual number I need to communicate". If the number is even bigger, we use 254 instead, meaning "read the next 4 bytes for the actual number", and if our number needs even more, we use 255, which implies the next 8 bytes are the actual representation of our number. Easy and efficient; most varints used in transactions never need to be more than one byte, but they can all grow to accommodate incredibly large numbers.
A Legacy Bitcoin Transaction
A "legacy" bitcoin transaction is the name we give a transaction that does not implement Segregated Witness, a newer form of transaction in which the "witness" data (fields 5 and 6 below) are put into their own special section (we say they are segregated, hence the name).
These legacy transactions are perfectly valid bitcoin transactions, but they are being used less and less because of the efficiency gains made by the segregated witness approach resulting in lower fees, as well as its fix of the transaction malleability bug, enabling, among others, the creation of lightning channels. Legacy transactions are easy to identify because they involve unlocking utxo(s) belonging to addresses starting with a 1.
This article breaks down a typical legacy transaction where one utxo is used and spent into two: one payment to a payee, and one payment to a change address. It contains 15 different fields, and I describe each of their purpose below.
[1] transaction version number
This field specifies the type of transaction being transmitted. It is of fixed-length (4 bytes) and is little-endian.
In our example:
01000000
The field indicates that this transaction is of version 1.
[2] number of inputs
This field expresses how many inputs will be unlocked by the transaction. Each of those inputs will need to be identified (here with fields 3 and 4), and unlocked (here with fields 5 and 6). In our case there is only one input, and so we only need to go through this loop once, but in the case where there are many inputs, we repeat the fields 3 to 6 as many times as there are inputs. This field is a varint, is little-endian, and can grow up to 9 bytes.
In Our Example:
01
The byte indicates that the transaction unlocks only one UTXO.
[3] previous transaction id
This field expresses the transaction which contains the output to be unlocked by the unlocking script in the coming fields 5 and 6. It is of fixed-length (32 bytes), and is little-endian.
In Our Example:
04dde43b0e4724f1e3b45782a9bfbcc91ea764c7cb1c245fba1fefa175c3a5d0
Because the field is little-endian, if you wish to search for that transaction in a block explorer you'll need to convert it to big endian first: d0a5c375a1ef1fba5f241ccbc764a71ec9bcbfa98257b4e3f124470e3be4dd04. A look at that transaction will reveal that there were 2 outputs to it. Which one of those two is unlocked by the signature script is defined in the next field.
[4] ouput number in previous transaction
Defining the transaction an output comes from is not precise enough—there might be more than one. We need to know which output from that transaction is being unlocked, and this field expresses that. It is of fixed-length (4 bytes), and is little-endian.
In Our Example:
01000000
This is the number 1 written in little endian, indicating that the output being unlocked is the second one in transaction d0a5c375a1ef1fba5f241ccbc764a71ec9bcbfa98257b4e3f124470e3be4dd04. It is valid for 300,000 satoshis, or 0.00300000 bitcoin.
[5] size of the unlocking script
This field indicates the number of bytes taken by the unlocking script, the field that follows it. It is a varint, and can take up to 9 bytes.
In our example:
6a
This byte is the hexadecimal representation of 106, meaning our unlocking script (field 6) will be 106 bytes long (212 hex characters).
[6] Unlocking script
You can think of the unlocking script as the key that unlocks the utxo. If any of the unlocking scripts fail for any of the input utxos, the whole transaction fails. If all unlocking scripts succeed, the signer has proven they have ownership of the coins, and the transaction can move forward to the next steps. This field is of variable length.
In our example:
4730440220519f7867349790ee441e83e545afbd25b954a34e0733cd4da3b5f1e5588625050220166730d053c3672973bcb2bb1a977b747837023b647e3af2ac9c15728b0681da01210236ccb7ee3a9f154127f384a05870c4fd86a8727eab7316f1449a0b9e65bfd90d
The unlocking script is written in a language called Script, a language unique to bitcoin. It is beyond the scope of this article to look at the exact unlocking script used in this transaction, but we know it was a valid script, since the transaction was indeed propagated by the network, and later on mined.
[7] sequence number
The sequence number is a field initially designed for a purpose it never fulfilled. Nowadays it is often disabled by setting it to ffffffff. It can used to signal that a transction is replace-by-fee enabled as per BIP 125, by setting the field equal to any number below ffffffff -1. In some cases, the field is used to set timelocks (to enable this, verion 2 of a transaction must be declared in field 1). It is of fixed-length (4 bytes) and is little-endian.
In our example:
ffffffff
The field is disabled in this transaction.
[8] number of outputs
This field expresses how many outputs the transaction will create. It is a varint.
In our example:
02
The transaction has two outputs.
[9] amount going to output 0
This field expresses the amount of bitcoin being locked in output 0, expressed in satoshis. It is a fixed-length field of 8 bytes, and is little-endian.
In our example:
5d36010000000000
Output 0 locks in 79,453 satoshis.
[10] size of locking script for output 0
This field expresses the size of the locking script for output 0. It is a varint.
In our example:
19
This byte is the hexadecimal representation of 25, meaning our locking script will be 25 bytes long (50 hex characters)
[11] locking script for output 0
This field is the locking script for output 0. It is a variable-length field.
In our example:
76a91478364a559841329304188cd791ad9dabbb2a3fdb88ac
We can think of this field as a of lock we put on output 0. It is written in Script, bitcoin's own programming language.
[12] amount going to output 1
This field expresses the amount of bitcoin being locked in output 1, expressed in satoshis. It is a fixed-length field of 8 bytes, and is little-endian.
In our example:
605b030000000000
Output 1 locks in 220,000 satoshis.
[13] size of locking script for output 1
This field expresses the size of the locking script for output 1. It is a varint.
In our example:
19
This byte is the hexadecimal representation of 25, meaning our locking script will be 25 bytes long (50 hex characters).
[14] locking script for output 1
This field is the locking script for output 0. It is a variable-length field. This is a variable-length field.
In our example:
76a914064e0aa817486573f4c2de09f927697e1e6f233f88ac
We can think of this field as a of lock we put on output 1. It is written in Script, bitcoin's own programming language.
[15] nLocktime
nLocktime field allows for a transaction to be unspendable until a certain point in the future. If the field is set to 00000000, the transaction is spendable right away. If they field is any number below 500 million, it is intepreted as a block height. If it is above 500 million, it is interpreted as a Unix timestamp. Transactions with locktimes on them will not be propagated by nodes if they are not valid at the time a node see it, hence the sender must wait until the transaction is valid before broadcasting.
In our example:
00000000
In our example the nLocktime field is such that the transaction is spendable right away.
Some notes on the above transaction
The example used here is a type of transaction known as a Pay to Public Key Hash, or P2PKH. It is the simplest form of transactions we see nowadays. The transaction hex has 450 characters, and the transaction is therefore 225 bytes in size.
TXID
The txid (transaction identifier) is derived from hashing the transaction data twice using SHA256. You can test this with our example transaction right in your shell. The following command basically takes the hex dump of the transaction, converts it to binary, hashes it, then converts that result to binary again, and hashes it once more. It is then printed to console in little-endian, hex format. Notice that you'll need to convert it to big-endian if you want to use it in a block explorer!
echo 010000000104dde43b0e4724f1e3b45782a9bfbcc91ea764c7cb1c245fba1fefa175c3a5d0010000006a4730440220519f7867349790ee441e83e545afbd25b954a34e0733cd4da3b5f1e5588625050220166730d053c3672973bcb2bb1a977b747837023b647e3af2ac9c15728b0681da01210236ccb7ee3a9f154127f384a05870c4fd86a8727eab7316f1449a0b9e65bfd90dffffffff025d360100000000001976a91478364a559841329304188cd791ad9dabbb2a3fdb88ac605b0300000000001976a914064e0aa817486573f4c2de09f927697e1e6f233f88ac00000000 | xxd -revert -plain | sha256sum | xxd -revert -plain | sha256sum
On Signing and Broadcasting
An often overlooked aspect of bitcoin transactions is how creating them and broadcasting them are two completely separate tasks, and that they can be done independently of each other. We mostly use wallets that construct and sign transactions and also broadcast them for us, but it does not have to be so.
This is what projects like TxTenna and the Lightning Network are leveraging.
That's it!
I hope this article proved to be an interesting way to peel the first layer on bitcoin transactions if you had not seen them this way before. More to come!
This content originally appeared on DEV Community and was authored by thunderbiscuit
thunderbiscuit | Sciencx (2021-05-06T00:38:55+00:00) Deconstructing a bitcoin transaction. Retrieved from https://www.scien.cx/2021/05/06/deconstructing-a-bitcoin-transaction/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.