This content originally appeared on Level Up Coding - Medium and was authored by Akhilesh Sharma

The following article put emphasis on the widely used tree traversal techniques (Breadth and Depth First Search). Before we dive into the implementation part of the traversals, I would like to go over minimal basics so that we understand what a Tree Data Structure looks like.
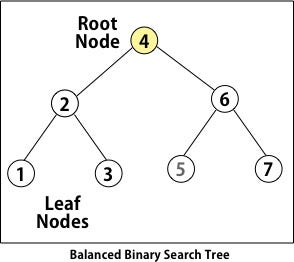
Trees
A Tree is a data structure composed of nodes. Each node is connected to other nodes in a top down manner.
The node at the top is considered as a Root Node. Root can have one or more children.
Nodes with no children are termed as “Leaf” Nodes.
Basic Tree Node Implementation
public class TreeNode{
public var val:Int
public var left: TreeNode?
public var right: TreeNode?
public init() {
self.val = 0
self.left = nil
self.right = nil
}
public init(_ val:Int) {
self.val = val
self.left = nil
self.right = nil
}
public init(_ val:Int,_ left:TreeNode?, _ right: TreeNode?){
self.val = val
self.left = left
self.right = right
}
}Depth First Search (DFS)
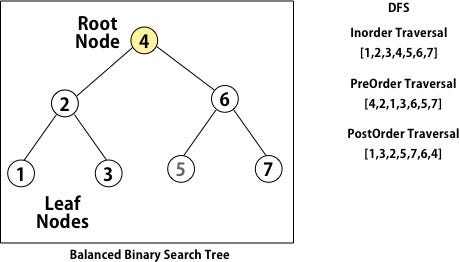
Depth first search is an algorithm to traverse through a tree in a particular pattern. The catch is that we keep traversing through the node in a particular pattern unless we reach the bottom of the tree.
There are different type of traversal that can be used within this algorithm but the overall concept remains the same.
Type of traversals
- In-Order — Left — Root — Right
- Pre-Order — Root — Left — Right
- Post Order — Left — Right — Root
DFS Implementation
//Inorder Traversal
var result:[TreeNode] = [TreeNode]()
func dfs_inorder(_ root: TreeNode?) -> TreeNode? {
if root == nil {
return root
}
dfs_inorder(root?.left)
if let root = root {
result.append(root)
}
dfs_inorder(root?.right)
return root;
}
// Preorder
func dfs_preorder(_ root: TreeNode?) -> TreeNode? {
if root == nil {
return root
} if let root = root {
result.append(root)
}
dfs_inorder(root?.left)
dfs_inorder(root?.right)
return root;
}
//PostOrder
func dfs_postorder(_ root: TreeNode?) -> TreeNode? {
if root == nil {
return root
}
dfs_inorder(root?.left)
dfs_inorder(root?.right)
if let root = root {
result.append(root)
}
return root;
}This covers up the implementation part about the Depth First Traversal in Trees. Remember to use recursion to traverse through the tree in case you want to perform a DFS. This is one of the most used traversal techniques when it comes to trees.
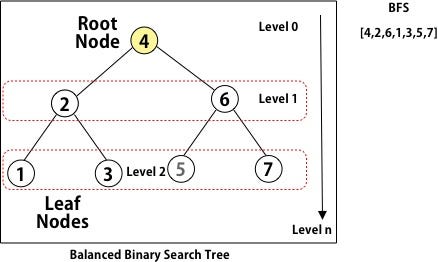
Breadth First Search (BFS)
BFS is another highly recommended traversal technique for Trees as well as Graphs. The node at the top of the tree is considered to be on the level zero and then it move forwards from top to bottom. The nodes in the tree are grouped on the basis of levels instead of depth.
Generally, there is a misconception of using recursion to implement BFS but instead this is implemented using Queues. It fairly simple if you understand the traversal algorithm.
BFS Implementation
var bfsResult:[Int] = []
func bfs(_ queue: inout [TreeNode], _ root: TreeNode?) {
guard let root = root else {return}
if queue.isEmpty {
queue.append(root)
}
while !queue.isEmpty {
var counter = queue.count - 1
while counter >= 0 {
let removedEl = queue.removeFirst()
bfsResult.append(removedEl.val)
if let left = removedEl.left {queue.append(left)}
if let right = removedEl.right {queue.append(right)}
counter -= 1
}
}
}
This covers the implementation details of BFS.
I hope this article helps you to understand the basics about the implementation of tree traversals using Swift. See you in the next post.
Happy coding! Cheers
Depth and Breadth First Search using Swift was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Akhilesh Sharma
Akhilesh Sharma | Sciencx (2021-05-07T23:23:31+00:00) Depth and Breadth First Search using Swift. Retrieved from https://www.scien.cx/2021/05/07/depth-and-breadth-first-search-using-swift/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
