This content originally appeared on DEV Community and was authored by seanpgallivan
This is part of a series of Leetcode solution explanations (index). If you liked this solution or found it useful, please like this post and/or upvote my solution post on Leetcode's forums.
Leetcode Problem #52 (Hard): N-Queens II
Description:
(Jump to: Solution Idea || Code: JavaScript | Python | Java | C++)
The n-queens puzzle is the problem of placing
nqueens on ann x nchessboard such that no two queens attack each other.Given an integer
n, return the number of distinct solutions to the n-queens puzzle.
Examples:
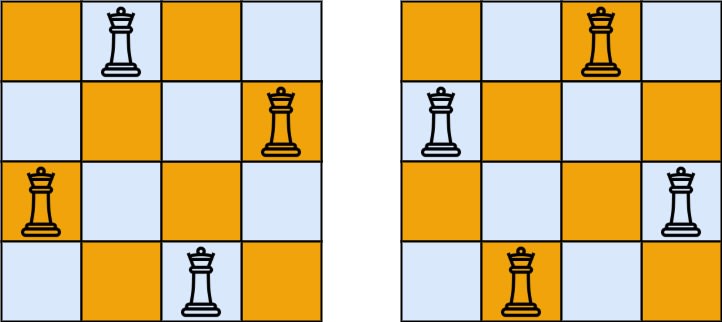
Example 1: Input: n = 4 Output: 2 Explanation: There are two distinct solutions to the 4-queens puzzle as shown. Visual:
Example 2: Input: n = 1 Output: 1
Constraints:
1 <= n <= 9
Idea:
(Jump to: Problem Description || Code: JavaScript | Python | Java | C++)
(Note: This problem is an easier duplicate to the previous problem, 51: N-Queens, except that it doesn't require us to return the actual boards, just the count.)
A naive approach here would attempt every possible combination of locations, but there are (N^2)! / (N^2 - N)! different combinations, which is up to ~1e17 when N = 9. Instead, we need to make sure we only attempt to place queens where it's feasible to do so, based on the instructions. This would seem to call for a depth first search (DFS) approach with a recursive helper function (place), so that we only pursue workable combinations without wasting time on known dead-ends.
First, we should consider how the queens will be placed. Since each row can only have one queen, our basic process will be to place a queen and then recurse to the next row. On each row, we'll have to iterate through the possible options, check the cell for validity, then place the queen on the board.
To decrease the space complexity of our solution, we can store the board as an array of integers representing each row, and use bit manipulation to store the presence of a queen in each row. To do so, we'll use the bitwise OR operator (|) to store a 1 in the bit to represent the queen's location in this row. Once the recursion returns, we can backtrack with a bitwise XOR operator (^) and iterate to the next cell in the row.
Since a queen has four axes of attack, we'll need to check the three remaining axes (other than the horizontal row, which our iteration will naturally take care of) for validity. There are N possible columns and 2 * N - 1 possible left-downward diagonals and right-downward diagonals. With a constraint of 1 <= N <= 9, each of the two diagonal states represents up to 17 bits' worth of data and the vertical state up to 9 bits, so we can use bit manipulation to store these states efficiently.
So for each recursive call to place a queen, we should pass along the board state in the form of only three integers (vert, ldiag, rdiag). We can then use bitmasks to check for cell validity before attempting to recurse to the next row.
Since our board is an N^2 matrix, we can use backtracking here to good effect. If we successfully reach the end of the board without failing, we should increment our answer counter (ans).
- Time Complexity: O(N!) which represents the maximum number of queens placed
- Space Complexity: O(N) for the board
Javascript Code:
(Jump to: Problem Description || Solution Idea)
var totalNQueens = function(N) {
let ans = 0,
board = new Uint8Array(N)
const place = (i, vert, ldiag, rdiag) => {
if (i === N) ans++
else for (let j = 0; j < N; j++) {
let vmask = 1 << j, lmask = 1 << (i+j), rmask = 1 << (N-i-1+j)
if (vert & vmask || ldiag & lmask || rdiag & rmask) continue
board[i] |= 1 << j
place(i+1, vert | vmask, ldiag | lmask, rdiag | rmask)
board[i] ^= 1 << j
}
}
place(0,0,0,0)
return ans
};
Python Code:
(Jump to: Problem Description || Solution Idea)
class Solution:
def totalNQueens(self, N: int) -> int:
self.ans, board = 0, [0] * N
def place(i: int, vert: int, ldiag: int, rdiag:int) -> None:
if i == N: self.ans += 1
else:
for j in range(N):
vmask, lmask, rmask = 1 << j, 1 << (i+j), 1 << (N-i-1+j)
if vert & vmask or ldiag & lmask or rdiag & rmask: continue
board[i] |= 1 << j
place(i+1, vert | vmask, ldiag | lmask, rdiag | rmask)
board[i] ^= 1 << j
place(0,0,0,0)
return self.ans
Java Code:
(Jump to: Problem Description || Solution Idea)
class Solution {
int ans;
int[] board;
public int totalNQueens(int N) {
ans = 0;
board = new int[N];
place(0,0,0,0);
return ans;
}
private void place(int i, int vert, int ldiag, int rdiag) {
int N = board.length;
if (i == N) ans++;
else for (int j = 0; j < N; j++) {
int vmask = 1 << j, lmask = 1 << (i+j), rmask = 1 << (N-i-1+j);
if ((vert & vmask) + (ldiag & lmask) + (rdiag & rmask) > 0) continue;
board[i] |= 1 << j;
place(i+1, vert | vmask, ldiag | lmask, rdiag | rmask);
board[i] ^= 1 << j;
}
}
}
C++ Code:
(Jump to: Problem Description || Solution Idea)
class Solution {
public:
int totalNQueens(int N) {
ans = 0;
board.resize(N, 0);
place(0,0,0,0);
return ans;
}
private:
int ans;
vector<int> board;
void place(int i, int vert, int ldiag, int rdiag) {
int N = board.size();
if (i == N) ans++;
else for (int j = 0; j < N; j++) {
int vmask = 1 << j, lmask = 1 << (i+j), rmask = 1 << (N-i-1+j);
if (vert & vmask || ldiag & lmask || rdiag & rmask) continue;
board[i] |= 1 << j;
place(i+1, vert | vmask, ldiag | lmask, rdiag | rmask);
board[i] ^= 1 << j;
}
}
};
This content originally appeared on DEV Community and was authored by seanpgallivan
seanpgallivan | Sciencx (2021-05-29T08:00:21+00:00) Solution: N-Queens II. Retrieved from https://www.scien.cx/2021/05/29/solution-n-queens-ii/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.