This content originally appeared on DEV Community and was authored by seanpgallivan
This is part of a series of Leetcode solution explanations (index). If you liked this solution or found it useful, please like this post and/or upvote my solution post on Leetcode's forums.
Leetcode Problem #118 (Easy): Pascal's Triangle
Description:
(Jump to: Solution Idea || Code: JavaScript | Python | Java | C++)
Given an integer
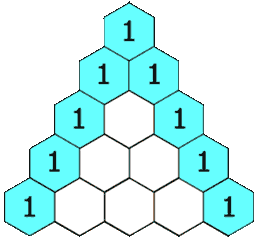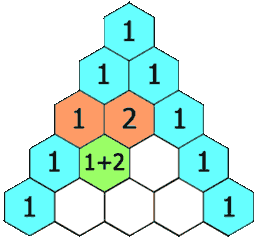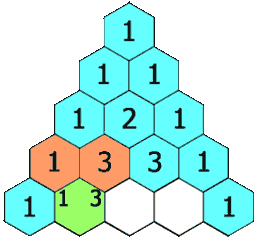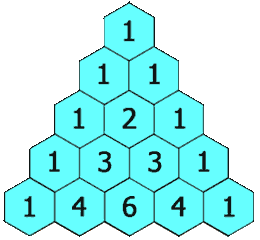
numRows, return the firstnumRowsof Pascal's triangle.In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
Examples:
Example 1: Input: numRows = 5 Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Example 2: Input: numRows = 1 Output: [[1]]
Constraints:
1 <= numRows <= 30
Idea:
(Jump to: Problem Description || Code: JavaScript | Python | Java | C++)
For this problem, we can do pretty much just as the instructions tell us. We'll iterate through the building of Pascal's triangle (ans), row by row. When we create each new row, we should initially fill it with 1s so that we don't have to worry about the logic of filling the edge cells that only have one number above.
Then we can start on j = 1 for each row and repeat the process of summing up the value of the current cell until we reach the midpoint (mid). Since the triangle is symmetrical, we can actually fill both halves of the row at once, while we work inward.
Once we reach the end of the last row, we can return ans.
- Time Complexity: O(N) where N is the numRowsth triangular number
- Space Complexity: O(1)
Javascript Code:
(Jump to: Problem Description || Solution Idea)
var generate = function(numRows) {
let ans = new Array(numRows)
for (let i = 0; i < numRows; i++) {
let row = new Uint32Array(i+1).fill(1),
mid = i >> 1
for (let j = 1; j <= mid; j++) {
let val = ans[i-1][j-1] + ans[i-1][j]
row[j] = val, row[row.length-j-1] = val
}
ans[i] = row
}
return ans
};
Python Code:
(Jump to: Problem Description || Solution Idea)
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
ans = [None] * numRows
for i in range(numRows):
row, mid = [1] * (i + 1), (i >> 1) + 1
for j in range(1, mid):
val = ans[i-1][j-1] + ans[i-1][j]
row[j], row[len(row)-j-1] = val, val
ans[i] = row
return ans
Java Code:
(Jump to: Problem Description || Solution Idea)
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> ans = new ArrayList<List<Integer>>(numRows);
for (int i = 0; i < numRows; i++) {
List<Integer> row = new ArrayList<>(i+1);
while (row.size() <= i) row.add(1);
int mid = i >> 1;
for (int j = 1; j <= mid; j++) {
int val = ans.get(i-1).get(j-1) + ans.get(i-1).get(j);
row.set(j, val);
row.set(row.size()-j-1, val);
}
ans.add(row);
}
return ans;
}
}
C++ Code:
(Jump to: Problem Description || Solution Idea)
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans(numRows);
for (int i = 0; i < numRows; i++) {
vector<int> row(i+1, 1);
int mid = i >> 1;
for (int j = 1; j <= mid; j++) {
int val = ans[i-1][j-1] + ans[i-1][j];
row[j] = val;
row[row.size()-j-1] = val;
}
ans[i] = row;
}
return ans;
}
};
This content originally appeared on DEV Community and was authored by seanpgallivan
seanpgallivan | Sciencx (2021-06-21T08:05:05+00:00) Solution: Pascal’s Triangle. Retrieved from https://www.scien.cx/2021/06/21/solution-pascals-triangle/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.