This content originally appeared on DEV Community and was authored by Ken Okabe
Current TC39 proposal Hack Pipeline Operator |> is incompatible with Grouping operator ().
Short version
Grouping operator ( )
The grouping operator
( )controls the precedence of evaluation in expressions.The grouping operator consists of a pair of parentheses around an expression or sub-expression to override the normal operator precedence so that expressions with lower precedence can be evaluated before an expression with higher priority.
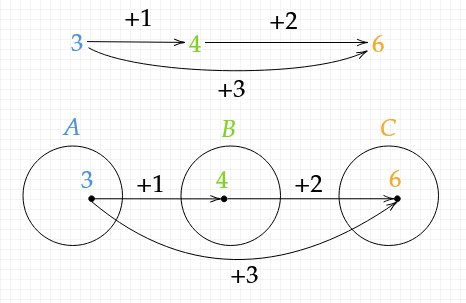
Test Code 1:
const f = a => a * 2;
const g = a => a + 1;
1 |> f(^) |> g(^);
1 |> (f(^) |> g(^));
Now we made (f(^) |> g(^)) to be evaluated before other expressions with higher priority.
I've investigated with Babel, and the transpiled result is the identical, which means:
(f(^) |> g(^)) is NOT evaluated before other expressions with the rule of Grouping operator ( ).
Does the current proposal Hack |> hijack the Grouping operator ?
Test Code 2:
Now I have a log function.
const right = a => b => b;
const log = a => right(console.log(a))(a);
This behaves like identity function: a => a
but, console.log(a) in the process.
Now, we want to know the evaluated value of (f(%) |> g(%))
1 |> (log(f(%) |> g(%)));
This should be totally fine because (f(%) |> g(%)) must have some value of the evaluation according to:
The grouping operator consists of a pair of parentheses around an expression or sub-expression to override the normal operator precedence so that expressions with lower precedence can be evaluated before an expression with higher priority.
The vanilla JS code is:
var _ref, _ref2, _ref3, _ref4;
const id = a => a;
const right = a => b => b;
const log = a => right(console.log(a))(a);
const f = a => a * 2;
const g = a => a + 1;
_ref2 = 1, (_ref = f(_ref2), g(_ref));
_ref4 = 1, log((_ref3 = f(_ref4), g(_ref3)));
and the result is:
3
Therefore,
1 |> (log(f(%) |> g(%)));
where (log(f(%) |> g(%))) == 3
1 |> (log(f(%) |> g(%)))
==
1 |> 3
???
and the evaluation value of whole 1 |> (log(f(%) |> g(%))) is 3
1 |> 3 == 3
I have no idea for this hack-pipe-operator, and simply think this has broken the laws of Mathematics, and more importantly, it seems the current proposal Hack |> hijacks the Grouping operator
The Babel implementation
https://github.com/tc39/proposal-pipeline-operator/issues/227#issuecomment-926136875
The Babel implementation has been done by @js-choi (one of the champions of the Hack pipes proposal).
The "reasonable stardard" is the spec proposal: either you learn how to read it (I'd be happy to help, if you are confused about any spec part), or you trust what who can read it says.
Issue
In fact, I made an issue for this.
Does the current proposal override the Grouping operator ( ) with Hack |> ? #229
https://github.com/tc39/proposal-pipeline-operator/issues/229

https://github.com/tc39/proposal-pipeline-operator/issues/229#issuecomment-926308352
As had been explained already, parentheses don't work the way you seen to think they do. The result you're getting from Babel is entirely correct and expected, with exactly the same precedence and execution order that you'd get from parenthesizing a sequence of additions.
As this question has been answered, I'm closing this thread.
Issue closed with the tag of invalid, well, I don't think so.
@js-choi has explained to me for sure:
https://github.com/tc39/proposal-pipeline-operator/issues/227#issuecomment-926317660
@js-choi explanation
Hm. Well…I don’t think anyone is admitting or covering anything up. But I’ll give it a shot; hopefully this will help a little. ^_^
Parentheses change grouping. But they never have changed evaluation order, which is always left to right, even outside of parentheses. This is how JavaScript (and many other programming languages) have always been:
function f () {
console.log('F');
return 3;
}
function g (x) {
console.log('G');
return x + 4;
}
function h (x) {
console.log('H');
return x * 7;
}
// This will print F then G then H, and it will result in 3 * 12, i.e., 36.
`f() * (g(1) + h(1))`
Note how the f() evaluates first even before (g(1) + h(1)), despite (g(1) + h(1)) being in parentheses. That’s why F still prints first before G and H.
Parenthesized expressions are not always evaluated first; expressions outside of the parentheses to the left are evaluated beforehand. This has how JavaScript (and many other languages like C and Lisp) have always been.
Parentheses change grouping. But they have never changed evaluation order, which is always left to right, even outside of parentheses. This is how JavaScript (and many other programming languages) have always been:
// f, g, and h have the same definitions above.
// This will print F then G then H, and it will result in 3 * 12, i.e., 36.
f() * (g(1) + h(1))
// This will also print F then G then H, and it will result in 7 * 7, i.e., 49.
f() |> (g(^) |> h(^))
Note how the f() evaluates first even before (g(1) + h(1)), despite (g(1) + h(1)) being in parentheses. That’s why F still prints first before G and H.
This is the same reason why f() |> (g(^) |> h(^)) causes f() to be evaluated before (g(^) |> h(^)).
Just like how f() * (g(1) + h(1)) causes f() to be evaluated before (g(1) + h(1)).
It’s just the old left-to-right evaluation rules. There aren’t any special grouping rules here. Parentheses change the grouping, but they never have changed execution order from anything other than left to right.
Hopefully that clears it up a little! I can understand why it might be a little confusing, but it’s just the old rules. Nothing is happening here except for the old JavaScript evaluation/parentheses rules. ^_^
(Actually, perhaps I should also edit MDN’s documentation to make this clearer. Maybe this old parenthesized-expressions-are-not-always-evaluated-first rule is tripping up many people learning JavaScript.)
My explanation
Notice the order "two", "three", "four" isn't affected by the parenthesis. Let's try (two() * three()) + four(). Surprise, it's still "two", "three", "four"! But now the final log is 10. That's because the operands are evaluated left to right, and this doesn't change. What changed was the evaluation of the operators.
Note how the f() evaluates first even before (g(1) + h(1)), despite (g(1) + h(1)) being in parentheses. That’s why F still prints first before G and H.
I observe, again, two of you share the same concept, and there are confusion of concepts . So I will explain to you. Hope it helps, really.
Confusion of concepts
The problem you illustrated is not for binary operator but evaluation strategy of JS that is eager-evaluation, in this evaluation strategy, f(x) is evaluated as soon as it is found from left to right, yes, you are only correct here.
The only "safe" place is right side of lambda expressions: such as a => f(a). In this case, even it's found by compiler f(a) is safe! will not be evaluated. (the same goes to function statement). Therefore the technique is used to emulate lazy-evaluation. Another exception is true || f(x) but false || f(x) will be evaluated once found. Try it.
Then point is, what you told us is nothing to do with the evaluation order of binary operator or Grouping operator ( ).
The eager evaluation strategy strictly follows the Algebraic rule. Well, if you can find anomaly, show me :) It follows the rule of operators including Grouping operator () with no exceptions. The eager evaluation of f(x) never hams Algebraic expression in JS. If both of you have explained as if eager evaluation of f(x) is the limit of the math in JS. That is the harmful explanation for us.
Sure in your code, we will have F G H or two three four order and so what? Does it break the rule of the math or algebraic structure? Nah..
Parentheses change grouping. But they never have changed evaluation order, which is always left to right, even outside of parentheses. This is how JavaScript (and many other programming languages) have always been:
So, this is a false statement.
The tricky word is: evaluation "order".
Note how the
f()evaluates first even before(g(1) + h(1))
So another tricky term should be : "before" or "after"
In mathematics, when we use the term "order" "before" "after", does it mean time series? No way.
Does it mean the order of the line of terminal console?
This logs:
"two"
"three"
"four"
14
Doesn't matter in terms of math structure.
What does matter is dependency network structure.
Binary operation is merely a syntax-sugar of binary function, and when you chain them, you fundamentally compose the functions.
For instance, when you enjoy + binary operation, you guys repeatedly told me "left to right", but fundamentally you do
This is Fold
https://en.wikipedia.org/wiki/Fold_(higher-order_function)
There are both left and right side fold, and usually we use foldLeft and if it's monoid the result is the same of both side.
As you seen, this is a Graph. Dependency graph
In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other. It is possible to derive an evaluation order or the absence of an evaluation order that respects the given dependencies from the dependency graph.
Remember dependency graph or structure is completely different concept of time order.
Hack pipe
Hack pipe, on the other hand, unlike eager evaluation strategy, this does break the math structure, and again this one overrides Grouping Operator ( ). I meant in dependency base. This problem is elaborated in my previous post #227 (comment)
I don't think it's on purpose, but the confusion of concept of Evaluation strategy and Algebraic structure is harmfully explained to justify the false design of Hack pipe that overrides the operator with the highest precedence in JS.
I will maintain my claim:
Does the current proposal override the Grouping operator ( ) with Hack |> ? #229
Deletion of my explanation
@js-choi
It’s just the old left-to-right evaluation rules. There aren’t any special grouping rules here. Parentheses change the grouping, but they never have changed execution order from anything other than left to right.
So this is a false statement.
So why there's no link to my explanation? Deleted by them.
https://github.com/tc39/proposal-pipeline-operator/issues/227#issuecomment-926737650
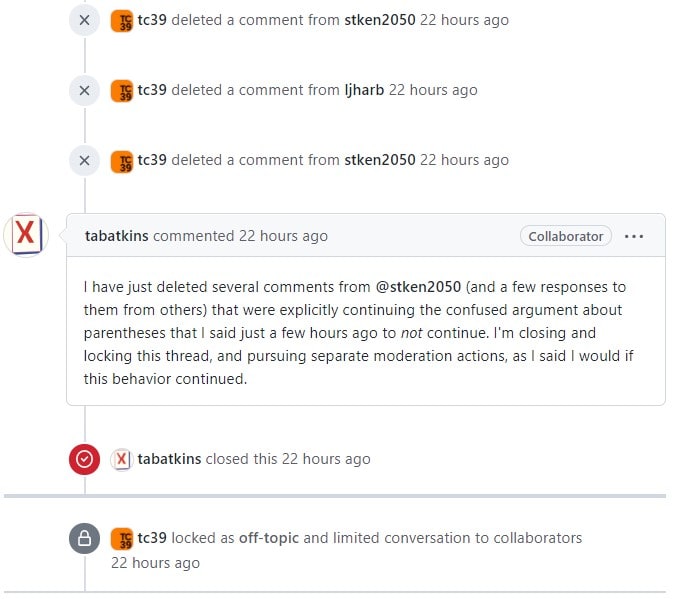
I have just deleted several comments from @stken2050 (and a few responses to them from others) that were explicitly continuing the confused argument about parentheses that I said just a few hours ago to not continue. I'm closing and locking this thread, and pursuing separate moderation actions, as I said I would if this behavior continued.
Long version
What is grouping-operator?
Grouping operator ( )
The grouping operator
( )controls the precedence of evaluation in expressions.The grouping operator consists of a pair of parentheses around an expression or sub-expression to override the normal operator precedence so that expressions with lower precedence can be evaluated before an expression with higher priority.
Grouping operator ( ) itself has the highest precedence in JavaScript.
Operator precedence
What is pipeline-operator?
In a general sense, pipeline-operator |> is a binary operator for function application that is equivalent to f(x)
f(x) == x |> f
Benefit of binary operator
Introducing a new binary-operator in JavaScript is nothing new.
In ES2016 , exponentiation operator ** has been introduced.
Math.pow(2, 3) == 2 ** 3
Math.pow(Math.pow(2, 3), 5) == 2 ** 3 ** 5
As you can see, a binary operator significantly improve the readability of a code, especially for the nesting structure of f() notation,
Essentially, pipeline-operator is the same league of the exponentiation operator, and the benefit is also common.
g(f(x) == x |> f |> g
Expectation of the community
In fact, pipeline-operator in JS has been expected from the community.
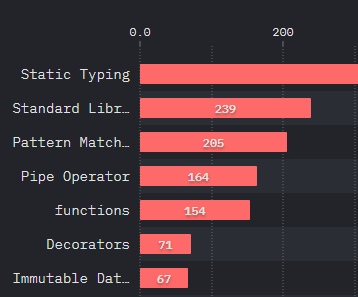
#StateOfJS 2020: What do you feel is currently missing from JavaScript?
- Static Typing
- Pattern Matching
- Pipe Operator
- functions
- Immutable Data Structure
It's reasonable to observe that the majority of the JS community has longed for more strictness of the language.
Especially for Static Typing:
Why Static Typing is so popular?
There is no native static type system in JavaScript, so currently, many use TypeScript instead.
So why do we like Type so much?
The general answer would be that we can avoid BUGs, in other words Type makes a code robust.
Why Type makes a code robust?
Because Type is mathematics.
I will explain briefly about Type since I think the understanding helps readers follow this discussion.
Types as Sets
Type == Sets
Type theory versus set theory
Alternately, we could change our terminology so that what we have been calling “types” are instead called “sets”.
Thus, words like “type” and “set” and “class” are really quite fungible. This sort of level-switch is especially important when we want to study the mathematics of type theory,
Types as Sets · An Introduction to Elm
In pursuit of this goal, I have found it helpful to understand the relationship between types and sets. It sounds like a stretch, but it really helps develop your mindset!
What is Sets?
Definition of Function
https://en.wikipedia.org/wiki/Function_(mathematics)#Definition
Intuitively, a function is a process that associates each element of a set X, to a single element of a set Y.
https://ncatlab.org/nlab/show/function
In a strict sense of the term, a function is a homomorphism f:S→Tf : S \to T of sets. We may also speak of a map or mapping, but those terms are used in other ways in other contexts.
So, in the definition of function, we need to define the sets of x and y
where y = f(x), or x |> y
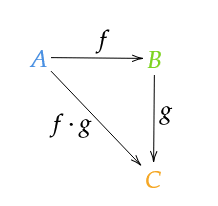
A binary operator is a syntax-sugar of binary functions
As you can see in the picture,
x * y == f(x, y)
or should I edit this picture to
A binary operator is a syntax-sugar of binary functions.
We also need to type (== sets) x and y or f correctly as the request from the mathematical definition of function, and according to the overwhelming popularity of Static Typing in the survey, that is what people want. They needs more strictness of JavaScript for their robust codes.
For x |> f === f(x), essentially it's clearly typed:
x : JavaScript Objects
f : Function
Then, since this is f(x), the type(==sets) of x should be defined along with the definition of f.
This is what people want.
Hack-style reached Stage-2
Recently, I have noticed JS pipeline-operator has reached TC-39 Stage-2, so I have examined:
tc39/proposal-pipeline-operator
Pipe Operator (|>) for JavaScript
Why the Hack pipe operator
There were two competing proposals for the pipe operator: Hack pipes and F# pipes. (Before that, there was a third proposal for a “smart mix” of the first two proposals, but it has been withdrawn, since its syntax is strictly a superset of one of the proposals’.)
The two pipe proposals just differ slightly on what the “magic” is, when we spell our code when using |>.
This proposal: Hack pipes
In the Hack language’s pipe syntax, the righthand side of the pipe is an expression containing a special placeholder, which is evaluated with the placeholder bound to the result of evaluating the lefthand side's expression. That is, we write value |> one(^) |> two(^) |> three(^) to pipe value through the three functions.
Pro: The righthand side can be any expression, and the placeholder can go anywhere any normal variable identifier could go, so we can pipe to any code we want without any special rules:
-
value |> foo(^)for unary function calls, -
value |> foo(1, ^)for n-ary function calls, -
value |> ^.foo()for method calls, -
value |> ^ + 1for arithmetic, -
value |> [^, 0]for array literals, -
value |> {foo: ^}for object literals, -
value |> `${^}`for template literals, -
value |> new Foo(^)for constructing objects, -
value |> await ^for awaiting promises, -
value |> (yield ^)for yielding generator values, -
value |> import(^)for calling function-like keywords, - etc.
What??
I had a hope for value |> f is still valid, but syntax-error.
The type of right hand side of |> is no longer function but something unknown.
Reactions
I investigated the issue of this proposal.
- #200: Added value of hack-style proposal against temporary variables https://github.com/tc39/proposal-pipeline-operator/issues/200
- #202: Separate (complementary) F# pipeline proposal? https://github.com/tc39/proposal-pipeline-operator/issues/202
- #205: Hack is dead. Long live F#. https://github.com/tc39/proposal-pipeline-operator/issues/205
- #206: Should enabling point-free programming/APIs be a goal of the Pipeline Operator? https://github.com/tc39/proposal-pipeline-operator/issues/206
In fact, #205: Hack is dead. Long live F#. has 199 comments and now closed by moderator.
https://github.com/tc39/proposal-pipeline-operator/issues/205#issuecomment-918717394
This is a huge thread and reading there, I've watched the issue was closed in real-time.
Here are few comments I've found around threads:
The future of functional programming is Hack pipe
Nope. It isn't. If this is truly what became added to the language I would continue to use Ramda's
pipe, which is a shame because I would really love to remove some overhead of installing a package in order to do something so simple.
I'm thinking ahead. JavaScript won't cease to exist once Hack reaches stage 4.
I would rather have the language remain without any pipe operator than to have to deal with Hack in the future.
I too would like to thank @js-choi and the other contributors for all their effort, but I believe the current direction to be misguided to the detriment of not just the FP community, but the JS community at large.
The argument against hack pipes is that we believe they are a hazard (sometimes for different reasons, but the conclusion is the same). Most of us in this thread and I suspect in the wild, would rather have no pipes, than hack pipes.
PFA proposal is a universal solution to those who worries about the arrow function noise on all three cases: map, then and pipe. If PFA is not ready, and we don't want minimal/F# without PFA, then let's wait, instead of introducing an irreversible Hack pipes.
And as I said, if PFA is stuck, then it's not a good reason to introduce Hack. We should either wait, or avoid pipe at all (or introduce minimal/f# style anyway).
Also, as a writer whose job is to communicate meaning, hack style removes my ability to provide descriptive names, which is basically the universal first step of writing readable code. I'm honestly shocked at this proposal. Imagine if you started at a new company and they enforced that all unary functions you write regardless of context had to name their single argument
x(or god forbid,^). That's how I feel and I'm not exaggerating - this proposal scares me because it's going to lead to code that is uglier, harder to read, and harder to refactor/abstract later on!
Edit: I too would rather see no pipe than this and am admittedly biased as I've always thought a pipe operator (or pretty much any more new syntax) is a bad idea. But if we are going to have it, I'd rather see it implemented in a way that improves readability, not (IMHO) hinders it.
I've found they claim it's far better not to have any pipe than to have hack-style because they evaluated the one harmful to JavaScript.
This is a comment by RxJS auhthor
https://github.com/tc39/proposal-pipeline-operator/issues/228#issuecomment-925465598
I've been told several influential members want to discourage point-free programming. Therefore, anything that might help functional programming libraries is unlikely to pass the TC39. It is what it is. It's the hack proposal or nothing. IMO, the hack proposal isn't useful enough to justify the additional syntax. But I'm not on the committee
Please don't @ me into these threads. I've said my piece. Pretty thoroughly. I wasn't really heard. And I lost a friend over it. I simply just don't care what happens with this anymore. If it passes, great. Unfortunately, I don't really have any use for the proposed pipeline operator. But I'm hopeful for other features someday that I will have a use for.
History of the proposal
I think it's fair to share the history posted by a project member @js-choi
Brief history of the JavaScript pipe operator
My study on Hack
In fact, I had to study the Hack-style-pipeline-operator.
I had no idea what this is.
For the minimal/F# proposal, it's merely x |> f === f(x) , so simple, no requirement to study.
I had joined issues, and also I've opened a couple of issues by myself, and actually lots of text here is copy&paste of my own comment there.
Pipeline-operator in a mathematical sense
Before I discuss Hack pipe, I share my knowledge on the pipeline-operator in a mathematical sense that is
x |> f === f(x)
Associative property and Monoid
Addition
https://en.wikipedia.org/wiki/Addition#General_theory
General theory
The general theory of abstract algebra allows an "addition" operation to be any associative and commutative operation on a set. Basic algebraic structures with such an addition operation include commutative monoids and abelian groups.
Here the important property is associative
(1 + 2) + 3 =
1 + 2 + 3 =
1 + (2 + 3)
JS String is also has associative property, and they are called Monoid in algebra.
In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element.
Associativity
For all a, b and c in S, the equation(a • b) • c = a • (b • c)holds.In computer science and computer programming, the set of strings built from a given set of characters is a free monoid.
What does this mean?
"Hello" + " " + "operator" ==
"Hello " + "operator" ==
"Hello" + " operator" ==
"Hello operator"
Strings and + the binary operator in JS is a Monoid, and as you know this String operator is very easy to use and robust.
Monoid or associative property has rock solid structure because it's hardly broken.
Imagine LEGO block, that is also Monoid, the order to construct block does not effect the result:
(A + B) + C =
A + B + C =
A + (B + C)
Any order to construction of the combination of LEGO bock reaches the identical result. So in software development if the entity has Monoid property, we can treat it as if LEGO block. That's the virtue of Monoid. Just its like LEGO, wonderful stuff.
Without the associative property, we will experience Combinatorial explosion.
In mathematics, a combinatorial explosion is the rapid growth of the complexity of a problem due to how the combinatorics of the problem is affected by the input, constraints, and bounds of the problem.
The history of software development is the war against complexity.
In fact, Associativity is one of the most important concept in programming and Associativity is the key to avoid the software complexity that is the fundamental reason of BUGs . In other words, as long as we are very carful to keep things with associative property, we safely can avoid complexity and obtain a bug-free code.
So Associativity is important, https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Exponentiation

They care a lot.
Function composition as a Monoid
https://en.wikipedia.org/wiki/Monoid
For example, the functions from a set into itself form a monoid with respect to function composition.
I will explain this.
One of "the functions from a set into itself" is addition.
// function from a set into itself
const f = a => a + 1; // f: number -> number
const g = a => a + 2; // g; number -> number
- please note I use the composition operator for g(f(x)) not
g.fbutf.g
a |> f |> g ===
a |> (f . g)
This is the simple structure of
Function application (pipeline-operator)
Function composition (composition-operator).
They are the both side of the same coin.
(f.g).h === f.g.h === f.(g.h)
Therefore, function composition is Monoid.
a |> f |> g |> h ===
a |> f |> (g . h) ===
a |> f . (g . h) ===
a |> (f . g) |> h ===
a |> (f . g) . h ===
a |> (f . g . h)
where f.g is the composition of f and g
(in traditional math style is g.f regarding g(f) but I don't use this style )
This is the whole picture you should know, and as you can see:
function application |> is not associative and not Monoid.
a |> f |> g !=
a |> (f |> g)
The (f |> g) does not make sense and the Type==Sets is violated in terms of x |> f.
However, this is what the Hack style is doing.
const f = a => a * 2;
const g = a => a + 1;
1 |> f(^) |> g(^); //3
1 |> (f(^) |> g(^)); //3
and (f(^) |> g(^)) is also evaluated as 3,
with the higher priority of general rule of Mathematics or grouping-operator ()
as a result
1 |> 3 == 3
This does not make sense at all, and the fundamental reason is they simply violates the rule of mathematics.
Monad
Pipeline-operator |> and function application does not have associative property in Monoid layer, but the form
a |> f |> g ===
a |> (f . g)
is also called Associativity in Monad layer.
https://wiki.haskell.org/Monad_laws
For your convenience, I would rewrite to
Associativity: (m |> g ) |> h === m |> (x => g(x) |> h)
or
Associativity: (m |> g ) |> h === m |> (x => x |> g |> h)
as (x => x |> g |> h) is the function composition of g and h
Associativity: (m |> g ) |> h === m |> (g . h)
For left-right identity,
with identify function: id= x => x
For every Function: f: A ->B
If this forms, the algebraic structure is called Monad.
Note: this corresponds to Monoid has associativity and identify.
Function Application |> Monad
Function Composition . Monoid also Monad (obvious, but prove by yourself)
So mathematically, |> is Monad, not Monoid.
Math structure of Hack pipe
F# pipe is simply mathematical function application, it behaves like Monad, so it's natural it does not behave Associative in Monoid.
Hack pipe, on the other had, it behave like Associative and Monoid,
a |> f(^) |> g(^) ==
a |> (f(^) |> g(^))
but this is not a monoid.
Something unknown to leads:
1 |> 3 == 3
This is something completely different from Function application in mathematical sense.
This one breaks the Algebraic structure that I've explained so far.
Function application is NOT Monoid and should not behave like Monoid.
Function composition is Monoid but with Hack pipe, there is no such a concept anymore because it has broken the mathematics.
With pipeline-operator in the algebraic sense,
a |> f |> g ===
a |> (f . g)
This is Associative in Monad layer with Function composition that itself is Associative and Monoid/Monad in both layers.
Type of Hack pipe
I'll give it another shot.
Since function application operator |> in algebraic sense is Monoid, perhaps we can replace this binary operator to another famous one *.
Then, perhaps we can replace function composition operator . to another Monoid +.
So, as a type,
A |> F |> F |> F is replaced to
A * F * F * F
===
A * (F + F + F)
where
(F + F + F) is the function composition.
This behaves as identical as the familiar behavior of the arithmetic.
Simple.
Hack on the other hand,
They claim the simplicity:
A * F * F * F
===
A * (F * F * F)
We no longer understand what the (F * F * F) is.
In fact, they say:
(F * F * F) itself is a syntax-error.
Sure it should be because it doesn't make sense, and
(F * F * F) is refused to be evaluated because they ignore the rule of grouping-operator.
In other words, they overrides a rule of the operator that has the highest precedence priority in JavaScript, that I would call hijack.
(F * F * F) is not a function composition like in F# or math pipe, nor anything understandable, so Type is ?
A * (?)
and (?) appears to be the evaluated value of the whole expression (such as 3):
? == A * (?)
therefore
A * (A * (A * (A * (A * (A * (A * (..?..)))))))
Some structure of infinite recursion.
That is the Type of the Hack pipe. Scary.
Hijacking grouping-operator ()
Internally, technically, the Hack |> refuses to evaluate (f(%) |> g(%)) first ignoring the rule of
Grouping operator ( )
The grouping operator consists of a pair of parentheses around an expression or sub-expression to override the normal operator precedence so that expressions with lower precedence can be evaluated before an expression with higher priority.
Grouping operator ( ) itself has the highest Operator precedence in JavaScript.
Then I hear the counter explanation to justify:
It’s just the old left-to-right evaluation rules. There aren’t any special grouping rules here. Parentheses change the grouping, but they never have changed execution order from anything other than left to right.
"old left-to-right evaluation rules" that means eager evaluation strategy of JavaScript follows the rule in the sense of both Mathematics and grouping-operator ().
Eager evaluation does not conflict to evaluation order.
The evaluation order arises from Dependency graph
In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other. It is possible to derive an evaluation order or the absence of an evaluation order that respects the given dependencies from the dependency graph.
and () defines the dependency graph and the structure of the code.
Remember dependency graph or structure is completely different concept of time order.
Here, in the terms of "evaluation order", "before", "after" we discuss Not time order of the evaluation/excision, but dependency structure of the code, which unfortunately it seems everyone in the Hack pipe proposal team share the confusion of the concept.
As we've seen, the Hack pipe refuses to follow the evaluation order of dependency structure and I would call this Hijacking grouping-operator ().
I did explain to them, but they did not hear, then deleted my explanation. That is why I made a post here.
Current TC39 proposal Hack Pipeline Operator |> has severe problems including the process of the staging, and the entire community of JavaScript will suffer.
This content originally appeared on DEV Community and was authored by Ken Okabe
Ken Okabe | Sciencx (2021-09-25T23:28:23+00:00) The current tc39/proposal-pipeline-operator Hack-style |> hijacks Grouping operator ( ). Retrieved from https://www.scien.cx/2021/09/25/the-current-tc39-proposal-pipeline-operator-hack-style-hijacks-grouping-operator/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.