This content originally appeared on DEV Community and was authored by Pedro Victor
Sumário
- TL;DR
- O problema inicial
- Como comparamos strings
- Uma ideia alternativa
- Idealizando um "autocomplete"
- Algumas otimizações
- Conclusão
TL;DR
Tries são estruturas de dados que assumem a forma de árvore de busca, podendo um nó ter diversos filhos, mas nunca mais de um pai. A chave de cada nó geralmente é composta por um único caractere, o caminho a partir da raiz até um determinado nó forma uma palavra, ou parte de uma, inserida na Trie.
Problema inicial
Imagine que estamos desenvolvendo um jogo cuja meta do jogador é escrever todas as palavras que conhece, ganha quem souber mais palavras! Uma forma de contabilizarmos as palavras inseridas pode ser: a cada inserção verificamos se a palavra já foi inserida em uma lista, caso não tenha sido então adicionamos.
De fato essa solução funciona, mas será que essa é realmente a mais interessante?
Um método geral para comparar strings
Antes de tudo, vamos entender como geralmente comparamos strings. Para isso, utilizando como linguagem o JavaScript e este link como fonte temos uma forma geral de comparar strings:
- Compare o primeiro caractere de cada string
- Caso o valor de Unicode da primeira string seja maior ou menos que o da segunda, sabemos que são strings diferentes e terminamos
- Caso sejam iguais, continue com o segundo caractere
- Efetue a mesma etapa incrementando o índice do caractere analisado até finalizar a string
- Caso cheguemos ao final da string e seus caracteres sejam iguais, sabemos com certeza que ambas as cadeias de caracteres são iguais
Uma ideia alternativa
A essa altura entendemos então que ao tentar adicionar uma palavra na lista que comentamos anteriormente não iremos apenas comparar ela N vezes, com N sendo a quantidade de palavras inseridas anteriormente na lista, mas por baixo dos panos também iremos comparar letras, palavra por palavra, de todos os elementos da lista.
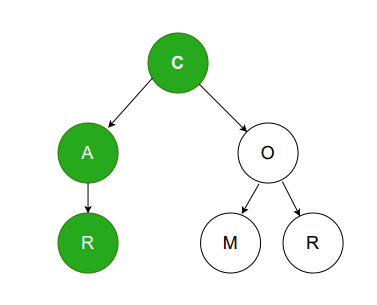
Temos então uma ideia! E se montarmos um conjunto com as palavras que começam com a letra "C"? Nesse caso, quando quisermos adicionar a palavra "Car" apenas temos que comparar com as palavras dentro deste conjunto, reduzindo as comparações com palavras que começam com outras letras. Podemos aplicar o mesmo raciocínio e, dessa vez, construir o conjunto das palavras que começa com "Ca", e assim caso este esteja vazio sabemos que a palavra "Car" não foi inserida anteriormente e, por tanto, basta adicionar!
Note que o conjunto anterior continha então as palavras "Com" e "Cor", agora, inserimos "Car".
Um caso de uso mais complexo
Imagine que um programador esteja digitando em seu editor de texto e você deseja fornecer uma opção de "autocomplete" que mostra as palavras-chave que o usuário pode estar querendo digitar. Nesse caso, temos C, um conjunto de palavras-chave da linguagem, S um "armazém" de Tries que contém essas palavras-chave e W, a palavra que o programador começou a digitar. Podemos, portanto, selecionar em S (nosso "armazém") a Trie cuja raiz tem chave igual à primeira letra de W (palavra que o programador digitou), chamaremos esta de T (entenda apenas como sendo a Trie que usaremos), e então percorremos a cada letra de W um nó em T e, ao fim de W, percorremos essa sub-árvore com raiz na última letra da palavra digitada e mostramos todas as palavras que podem ser formadas a partir dela!
Parece complicado né? Mas na verdade não é! Entenda que nosso armazém é na verdade a raiz de uma Trie! Estranho né? Mas apenas pense que seria o equivalente de termos como chave nada mais nada menos que a string vazia, afinal, ela é prefixo de toda palavra!
Sobre o restante, nada mais é do que percorrer uma árvore a partir de um certo nó, o que podemos facilmente fazer com um pouquinho de conhecimento sobre a estrutura de dados árvore!
Nesse exemplo, suponha que o programador digitou apenas "L", dessa forma podemos percorrer recursivamente a Trie e obter para o nosso "autocomplete" as palavras-chave "Let", "List", "Length". Suponha agora que a entrada seja "Le", nesse caso teremos como retorno para "autocomplete" as palavras-chave "Let" e "Length". Com esse exemplo fica fácil saber como implementar, né?
Algumas otimizações
Suponha que no exemplo da imagem anterior tínhamos a palavra "Como", ao invés de "Com", dessa forma, naturalmente, poderíamos ter nossa Trie se adicionássemos um novo nó com a letra "o" como chave, correto? Sim!
Mas será que isso realmente é necessário? Algumas implementações utilizam uma breve otimização no quesito memória, como o nó de chave "m" não tem mais de um filho, poderíamos concatenar ambas as chaves e ter um nó de chave "mo". Isso traz alguma complexidade para a implementação, entretanto, representa um nó a menos na memória.
Tries podem ser implementadas de diversas formas, com diversos nomes, como: Árvore Prefixo, Árvore Sufixo e Árvore Patricia, cada um com seus detalhes de implementação e otimizações, é aconselhável ler o que cada uma tem a oferecer antes de implementar!
Conclusão
Com isso vemos uma nova forma de comparar strings, sem precisarmos percorrer repetidamente uma lista inteira, ou utilizar "índices únicos" em bancos de dados. Obviamente temos casos específicos para seu uso, o intuito deste artigo é apontar para uma nova abordagem, bem como uma nova estrutura de dados, caso algo não tenha ficado claro ou notou algum erro, não deixe de avisar!
This content originally appeared on DEV Community and was authored by Pedro Victor
Pedro Victor | Sciencx (2021-12-21T16:38:48+00:00) Como funcionam as Tries. Retrieved from https://www.scien.cx/2021/12/21/como-funcionam-as-tries/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.