This content originally appeared on DEV Community and was authored by sachin26
Hi,devs
Today we are going to learn about the Selection Sort algorithm, How it works, and what are the pros & cons of using this algorithm. In this article, we will also measure the Time Complexity & Space Complexity of this algorithm.
Selection Sort
The main idea of this algorithm is to find the minimum ( for ascending order ) or maximum( for descending order ) element from the unsorted array and put it at the beginning of the unsorted array.
let's visually understand this algorithm.
step-1 find a minimum element from the unsorted array.
To find the minimum element from the array, set the first element as a minimum from the unsorted array.
repeatedly compare minimum to unsorted elements and, if minimum < unsorted element, then update the minimum.
element 4 is less than minimum, then we update the minimum as 4.

element 2 is less than minimum, then we update the minimum as 2
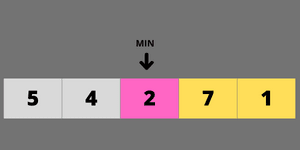
element 7 is not less than the minimum, so we will not update the minimum.
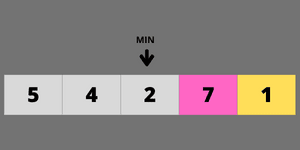
element 1 is less than minimum, then we update the minimum as 1.

so, 1 is the minimum element from the unsorted array.
step-2 swap minimum with beginning element of the unsorted array.
repeat these steps, until the array is entirely sorted.
after repeating the steps, Array looks like this.
See the Java solution.
Java
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{3,2,1,5,9};
System.out.println("unsorted Array : "+Arrays.toString(arr));
selectionSort(arr);
System.out.println("sorted Array in ascending order : "+Arrays.toString(arr));
}
private static void selectionSort(int[] arr){
int minIndex;
for(int i=0; i<arr.length;i++){
minIndex = i;
for(int j =i+1;j<arr.length;j++){
if(arr[j] < arr[minIndex]){
minIndex = j;
}
}
swap(arr,i,minIndex);
}
}
private static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
Pros & Cons
good for the smallest data or Array.
perform badly on large Array.
it will not take more than n swaps.
this algorithm requires no extra memory space except temp variables.
Time & Space Complexity
Time Complexity :-
for the first time, finding the minimum element from the unsorted array required n-1 comparisons. for the second time n-2 comparisons, then so on.
so, the overall time complexity is O(n2)
Space Complexity :-
Selection sort does not require any extra memory for sorting.
then, Space Complexity is O(1)
Thank you for reading this article. share this article with your dev friends and save it for the future.
This content originally appeared on DEV Community and was authored by sachin26
sachin26 | Sciencx (2022-01-06T10:46:25+00:00) Sorting Algorithms – #1 Selection Sort. Retrieved from https://www.scien.cx/2022/01/06/sorting-algorithms-1-selection-sort/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.




