This content originally appeared on DEV Community and was authored by sachin26
hi👋Devs,
I hope you getting some things from this Sorting Algorithms series.
in this article, we will discuss the very efficient and fast algorithm, Merge Sort algorithms.
Merge Sort
Merge Sort algorithm is based on the divide & conquer principle which states that repeatedly breaks down the problem into sub-problem, solves each sub-problem individually, and combines the sub-problem solutions into a final solution.
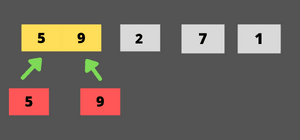
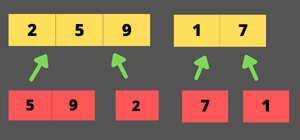
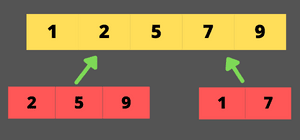
Let's understand this algorithm in a much better way with an example.
step-1 find the mid point and recursively divide the array into two subarrays until the array size becomes 1.
step-2 merge the two subarrays into an array till the final array is merged, in ascending order.
Pseudocode for recursively divide the array into two sub-arrays.
step-1 initialise left & right index of an array.
step-2 return if array size is 1.
if left >= right return.
step-3 find the mid of the array.
mid = (left + right) / 2
step-4 divide the array into two sub-array.
divide( array, left, mid)
divide( array, mid+1, right)
step-5 merge the two sub-array into a array.
marge( array, left, mid, right)
Pseudocode for merge the two sub-arrays.
step-1 calculate the size of left & right sub-arrays.
leftArrSize = mid - left+1
rightArrSize = right - mid
step-2 initialise the temps arrays for left & right sub-arrays
leftArr[]
rightArr[]
step-3 copy sub-arrays into the temp arrays.
leftArr[] = array[left....mid]
rightArr[] = array[mid+1...right]
step-4 set initial indexes of subarrays & array.
leftPointer = 0
rightPointer = 0
arrPointer = left
step-5 copy the temp sub-arrays into an array, in ascending or descending order, till the end of any temp sub-arrays.
step-6 copy the remaining elements of temp sub-arrays.
see the java implementation
Java
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{5,9,2,7,1,10,4,1,50};
System.out.println("unsorted Array : "+Arrays.toString(arr));
margeSort(arr,0,arr.length-1);
System.out.println("sorted Array in ascending order : "+Arrays.toString(arr));
}
private static void margeSort(int[] arr,int left,int right){
// return if arr size becomes 1
if(left >= right) return;
// calculate the mid
int mid = ( left + right ) / 2;
// divide the array into two subarrays
margeSort(arr,left,mid);
margeSort(arr,mid+1,right);
// merge subarrays
merge(arr,left,mid,right);
}
private static void merge(int[] arr,int left,int mid,int right){
// calculate the size of left & right subarrays
int leftArrSize = mid - left+1;
int rightArrSize = right - mid;
// initialise temp subarrays
int[] leftArr = new int[leftArrSize];
int[] rightArr = new int[rightArrSize];
// copy left & right array into temp arrays
for (int i = 0; i < leftArrSize; ++i)
leftArr[i] = arr[left + i];
for (int j = 0; j < rightArrSize; ++j)
rightArr[j] = arr[mid + 1 + j];
// set initial indexes of subarrays
int leftPointer = 0;
int rightPointer = 0;
int arrPointer = left;
// copy temp subarrays, in ascending order
while(leftPointer < leftArrSize && rightPointer < rightArrSize ){
if(leftArr[leftPointer] <= rightArr[rightPointer]){
arr[arrPointer] = leftArr[leftPointer];
arrPointer++;
leftPointer++;
}else{
arr[arrPointer] = rightArr[rightPointer];
arrPointer++;
rightPointer++;
}
}
// copy the remaining elements of left subarray into a marge array
while(leftPointer < leftArrSize){
arr[arrPointer] = leftArr[leftPointer];
arrPointer++;
leftPointer++;
}
// copy the remaining elements of right subarray into a merge array
while(rightPointer < rightArrSize){
arr[arrPointer] = rightArr[rightPointer];
arrPointer++;
rightPointer++;
}
}
}
Thank you for reading this article. share this article with your dev friends and save it for the future.
This content originally appeared on DEV Community and was authored by sachin26
sachin26 | Sciencx (2022-01-09T12:18:58+00:00) Sorting Algorithms – #3 merge Sort. Retrieved from https://www.scien.cx/2022/01/09/sorting-algorithms-3-merge-sort/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.