This content originally appeared on DEV Community and was authored by Gopi Gorantala
In this coding problem, we need to find the power-set of given input without duplicates.
Introduction
In this article, we discuss the subsets of a given input. This is one of the most popular questions asked in coding interviews.
Companies that have asked this in their coding interview are Apple, Microsoft, Amazon, Facebook, and many more.
Problem Statement
We need to write a program that finds all possible subsets ( the power set) of a given input. The solution set must not contain duplicate subsets.
Example 01:
Input: [1, 2, 3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
Example 02:
Input: [100]
Output: [[], [100]]
Explanation: The subsets of any given input are equal to its power set.
if, input n = 3, then, powerset => 2^n = 2^3 = 8.
Assume input has a length greater than or equal to 1.
Hint: Use the left-shift operator to achieve this.
Thought Process
In this program, we find the power set of a given input using bitwise operations.
In general, if we have n elements then the subsets are 2^n subsets.
So for every possible case of having at least two elements, we can see that an element is present and not present in the subsets.
Think of a solution that is iterative, uses bitwise operators, and generates the powerset.
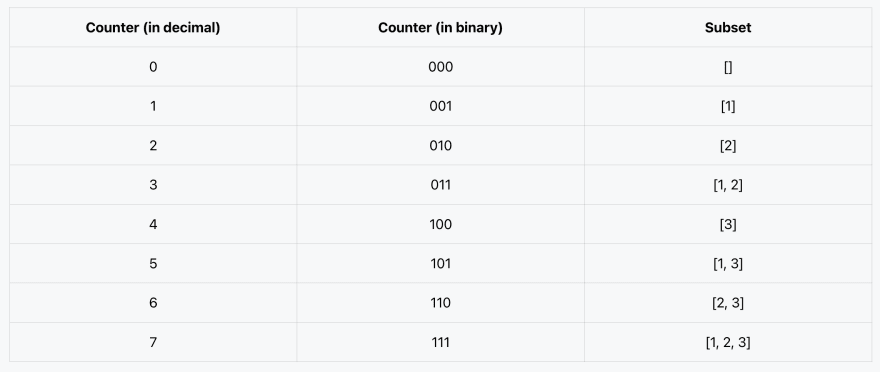
Here is how we generate each subset using the outer-loop variable counter. Here is a table indicating how the value gets generated based on the counter input.
Algorithm
We need to consider a counter variable that starts from 0 to 2^n - 1.
For every value, we are considering the binary representation and here we use the set bits in the binary representation to generate corresponding subsets.
If all set bits are
0, then the corresponding subset is empty[].If the last bit is
1, then we put1in the subset as[1].
Steps:
We use two loops here, the outer-loop starts from 0 to 2^n - 1, and the inner loop continues to input array length n.
In the inner loop, we conditionally check (counter & (1 << j)) != 0), if yes, then we print the corresponding element from an array.
Solution
#include <iostream>
#include <vector>
using namespace std;
void subsets(vector<int>& nums){
int n = nums.size();
int powSize = 1 << n;;
for(int counter = 0; counter < powSize; counter++){
for(int j = 0; j < n; j++){
if((counter & (1 << j)) != 0){
cout<<"[" <<nums[j] << "]";
}
}
cout<<endl;
}
}
int main() {
vector<int> array = { 1, 2, 3 };
subsets(array);
}
Complexity Analysis
Time Complexity: O(n*2^n), time complexity is n times the powerset.
*Space Complexity: * O(2^n), We are storing 2^n subset elements in an array. So the extra space is directly proportional to O(2^n).
This content originally appeared on DEV Community and was authored by Gopi Gorantala
Gopi Gorantala | Sciencx (2022-02-19T02:49:44+00:00) Subsets / Power Set – C++ Solution. Retrieved from https://www.scien.cx/2022/02/19/subsets-power-set-c-solution/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.