This content originally appeared on Level Up Coding - Medium and was authored by Ruslan Rakhmedov

Task description:
You are given a binary string s and a positive integer k.
Return the length of the longest subsequence of s that makes up a binary number less than or equal to k.
Note:
- The subsequence can contain leading zeroes.
- The empty string is considered to be equal to 0.
- A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
Example 1:
Input: s = "1001010", k = 5
Output: 5
Explanation: The longest subsequence of s that makes up a binary number less than or equal to 5 is "00010", as this number is equal to 2 in decimal.
Note that "00100" and "00101" are also possible, which are equal to 4 and 5 in decimal, respectively.
The length of this subsequence is 5, so 5 is returned.
Example 2:
Input: s = "00101001", k = 1
Output: 6
Explanation: "000001" is the longest subsequence of s that makes up a binary number less than or equal to 1, as this number is equal to 1 in decimal.
The length of this subsequence is 6, so 6 is returned.
Constraints:
- 1 <= s.length <= 1000
- s[i] is either '0' or '1'.
- 1 <= k <= 10^9
Reasoning:
A couple of things are worth mentioning. We need to find subsequence and not a substring. It means we can pick any bit from any position, but we cannot change their relative position in the initial input. Using this example “1001010” we can create subsequences like: “1001”, “111”, “0000”. At the same time we cannot create subsequence “100001” because we don’t have a pair of 1’s which has 4 0’s between them.
The maximum value of K is 1_000_000_000 which can be fit in Java’s integer.
Solution:
This task is a good example of where we can apply the “greedy” approach. We’re required to find a binary substring which is a subsequence of S and has a value ≤ K. 0 can be represented as 1000 of 0’s bits. Which means we can count all the zero bits we have in our input. At the same time we can create an array for keeping track of 1 bits:
boolean[] bits = new boolean[s.length()];
int zeroes = 0;
for (int i = 0; i < s.length(); i++)
{
if (s.charAt(i) == '1')
{
bits[i] = true;
}
else
{
zeroes++;
}
}
It doesn’t matter how many zeroes and from which positions we pick them, we are going to pick all of them and set it as an answer. Considering the max length of the input we can get 1000 bits which we cannot fit nether in integer nor in long. But the K’s max value says that we don’t need to worry about the number greater than Integer.MAX_VALUE. To do so we just are working with long. Having an array with marked positions of 1’s and knowing how many 0’s we’re given we’re going to greedily pick 1s moving from right to left in our input. Along the way we need to add new value to num and check for boundaries.
int res = zeroes;
long num = 0;
for (int i = bits.length - 1, j = 0; i >= 0; i--, j++)
{
if (bits[i])
{
if (num + (1L << j) > k)
{
break;
}
else
{
num += (1L << j);
res++;
}
}
}
To help you further understand the logic let me walk you through simple example. Let’s say we have this input “00101001”.
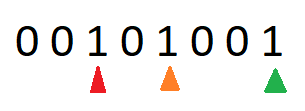
We have 5 zeroes and add them to our answer. The 1’s with the green triangle is 1 bit shifted to 0 positions(2 ^ 0) to the left gives us 1. The 1’s with the orange triangle is 1 bit shifted to 3 positions(2 ^ 3) to the left gives us 8. The 1’s with the red triangle is 1 bit shifted to 5 positions(2 ^ 5) to the left gives us 32.
Now depending on the K value, we can answer the task we’re given. As we have a number of zeroes and we know how to build the answer bit by bit. So the solution to the task looks like this
public int longestSubsequence(String s, int k)
{
boolean[] bits = new boolean[s.length()];
int zeroes = 0;
for (int i = 0; i < s.length(); i++)
{
if (s.charAt(i) == '1')
{
bits[i] = true;
}
else
{
zeroes++;
}
}
int res = zeroes;
long num = 0;
for (int i = bits.length - 1, j = 0; i >= 32; i--, j++)
{
if (bits[i])
{
if (num + (1L << j) > k)
{
break;
}
else
{
num += (1L << j);
res++;
}
}
}
return res;
}
The code above gives us good results. It has linear time and space complexity.

Java algorithms: Longest Binary Subsequence Less Than or Equal to K (LeetCode) was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Ruslan Rakhmedov
Ruslan Rakhmedov | Sciencx (2022-06-20T11:33:53+00:00) Java algorithms: Longest Binary Subsequence Less Than or Equal to K (LeetCode). Retrieved from https://www.scien.cx/2022/06/20/java-algorithms-longest-binary-subsequence-less-than-or-equal-to-k-leetcode/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
