This content originally appeared on Level Up Coding - Medium and was authored by Can Bayar
This story will be a little different from my regular posts. First of all, I need to say that each entry in this list goes deeper than it is written here and deserves an individual post. However, since I don’t have that much time and have seen that people really like to read lists of stupid things they can quickly digest, I decided to give this clickbait title format a chance. I have a four-hour train ride ahead of me and will try to complete it before I arrive at my destination.

Here, I bundled a bunch of things together that at least a few of them are likely to be unknown to most of you. There is no actual connection between the entries, other than they share the same thread of being so ordinary that you would never expect the problems you may have to face one day.
So, here is my list of 5 stupid things that have more complex underlying working mechanisms than you knew.
1. Floating-Point Arithmetic
This first one is rather a curious case and it is concerning float and double primitive types. Floating-point types are so simple, so ubiquitous that you don’t need to think twice before diving into performing operations with them. Yet, uncounted software developers remain oblivious that floating-point arithmetic is full of pitfalls that will bite you if you are careless.
Have you ever experienced something like this?
float x = 13.438;
float y = 4.562;
cout << "Result: " << x + y << endl;
------------------------------------
> Result: 17.99999999997
Let me guess, you have and the first time it happened it surprised you but you have been seeing this behaviour for so long that you just don’t care anymore because that’s the way things are. I am pretty sure you will start caring when this happens (and trust me, it will happen):
if (x + y == 18) {
cout << "Yay!" << endl;
} else {
cout << "Oh crap!" << endl;
}--------------------------------
> Oh crap!
If you were dealing with computer graphics, you would be dealing with these kinds of floating-point errors all the time. To understand floating-point arithmetic, first, you need to understand how the floating-point numbers are stored.
Visit your middle-school mathematics information for a while. You learned that there are infinitely many numbers between numbers 0 and 1. How are you supposed to represent infinitely many numbers by a finite number of bits? A float consists of 32 bits and a double consists of 64 bits. So, you can only represent a finite number of real numbers, unless you have unlimited space.
Your ancestors — the nerd ones, not the ones who crafted wooden tools to hunt animals — came up with a neat trick to represent floating-point numbers. They divided the bits into three partitions: sign, exponent and fraction.
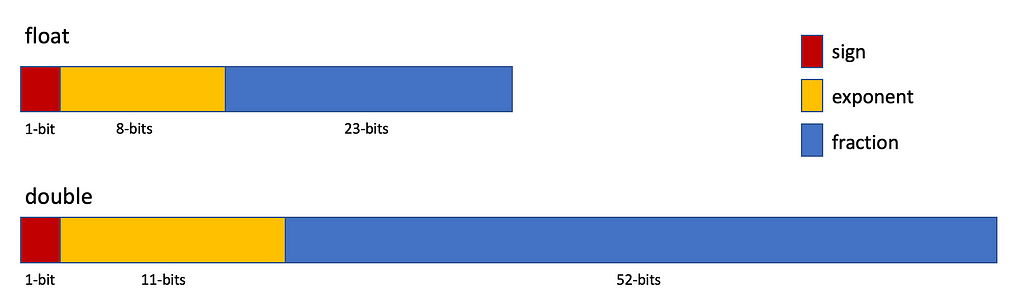
Then it is calculated according to a formula:
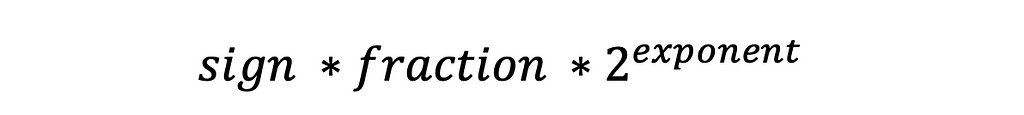
So, the floating-point numbers are represented as -1.56473 * ²³. Since not all real numbers are representable as floats or doubles, you need to be cautious operating with them. >and<operators would still work as intended, but you have to be extra careful when you are doing equals checks.
One common strategy to check equality among floating-point numbers is to use an epsilon value that tolerates a little amount of precision error. The amount you assign to the epsilon variable depends on your application needs, but it works like this:
final float EPSILON = 0.00001;
float x = ...
float y = ...
if (abs(x - y) < EPSILON) {
return true;
}That way you can get away with ignorable precision errors. At this point, it is very important to understand that you should never use floats and doubles when the precision is important, in order to represent money for example. A lot of programming languages support the BigDecimal interface for these kinds of operations, which uses strings and works slower but guarantees that the results are exact. You can also simply use integers and then format them when you need to print something.
2. Random Number Generation
Just like floating-point numbers, random numbers are frequently used in our daily development activities. And just like floating-point numbers, random numbers have a more complex inner logic than at first glance.
Most programming languages support an API to generate random numbers and all we need to do is to call the corresponding function. If you are using C++, all you need to do is
int value = rand();
The Java version is not very different:
int value = random.nextInt();
A lot of programming languages are packed with this kind of standard API functionalities to make your life easier. The downside is that a lot of software engineers tend to overlook these concepts since they are simply handed on a silver platter. But how does a computer generate random numbers? You may want to think a little while first before moving on…
Random number generation is actually a very hard problem in computer science. The reason is, that generating a sequence of statistically independent numbers is a non-deterministic job but the computers we use are deterministic, meaning that you always end up with the same outcome for the same input conditions. For this reason, you cannot generate truly random numbers without the help of some embedded devices that use constantly changing physical world data. This behaviour is practically impossible to model in our computers since there are infinitely-many conditions.
Instead, we use pseudo-random number generators (PRNG). The numbers they generate look random but are actually predetermined and mathematically calculated. You feed the PRNG with an initial seed and every value in the random number sequence is calculated according to the given formula. This means that, as long as you know the seed and the state of the PRNG, you can determine every value that will be generated by that function.
The linear congruential method is widely used to generate the values. The formula looks like this
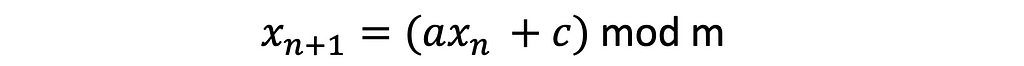
in which, x₀ is the function seed.
It is important that you understand the difference between true randomness and pseudorandomness. PRNGs usually suffice for your generic daily coding needs. Beware though, they are very predictable and will not be able to fulfil your more complex needs. For example, randomness is very important for cryptographically secure applications and you should use more sophisticated methods unless you want your application to be compromised.
3. Row-Major & Column-Major Ordering
Even a simple array traversal could become problematic if you don’t know how data is stored in the memory.
Row-major and column-major order are about how the multidimensional arrays are stored in the memory. Consider the 2D array given below:
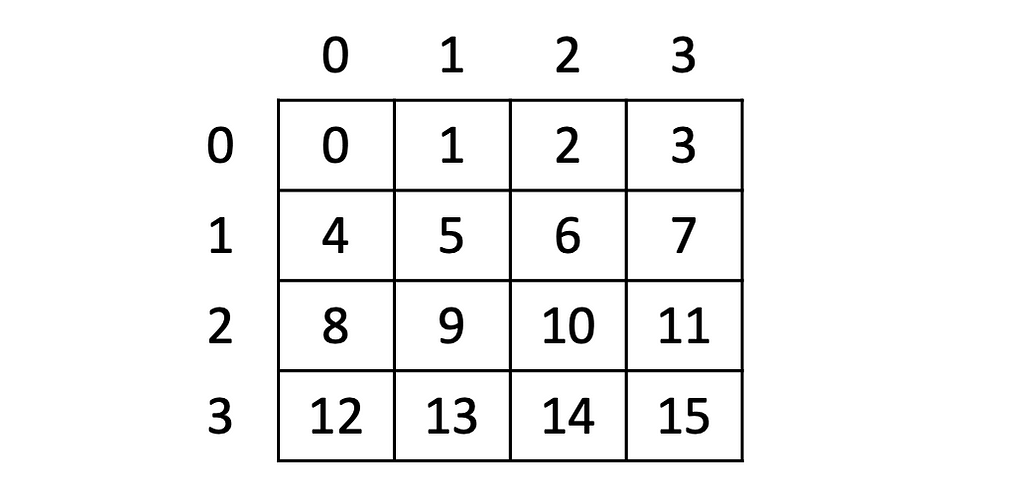
In row-major ordering, consecutive elements in a row are stored contiguously in the memory as given in the figure below.

The same thing is true for the columns in column-major ordering.

Some programming languages like C++ use row-major order while others like Fortran use column-major order. Depending on the programming language you use, how you traverse multi-dimensional arrays will affect the performance of your algorithm since accessing consecutive locations in the memory works faster.
Row-major order works faster when you access the elements row by row:
for (int i = 0; i < rowCount; i++) {
for (int j = 0; j < colCount; j++) {
int element = arr[i][j];
// Do something
}
}Likewise, column-major order works faster column by column:
for (int i = 0; i < colCount; i++) {
for (int j = 0; j < rowCount; j++) {
int element = arr[j][i];
// Do something
}
}4. Endianness
Data representation may change over the network and you need to deal with it. Otherwise, you may end up with misinterpreted messages.
Endianness is the order of the bytes of data stored in the memory. We will face two choices, little-endian and big-endian. Let’s use the random integer 1682348653, which is equal to 0x64469A6D in hexadecimal.
- A little-endian system stores the most significant byte at the biggest address.

- A big-endian system stores the most significant byte at the smallest memory address.

Basically, the big-endian is reading from left to right whereas the little-endian is reading from right to left.
Dealing with endianness can be problematic. If you are writing a low-level serialization/deserialization algorithm for network transmission for example, you need to make sure that you use the same method on both sides of the communication, otherwise, you will end up with the wrong data.
5. Branch Prediction
In modern programming languages, we use the if-statements abundantly, since they only haveO(1)algorithmic complexity. But algorithmic complexity can be deceptive. In practice, an O(nlogn) algorithm may work faster than an O(n) algorithm depending on the operations it does. And branching is not that costless on the assembly level.
How does branching work on the assembly level? You see, every time we go through an if-statement, the processor needs to decide whether to do a conditional jump to a different statement or just execute the following. But how is this decision slows down the execution? Because the processors use pipelining, running instructions parallel in order to increase the throughput. When the processor encounters a conditional jump, it simply doesn’t know which instruction will be added to the pipeline.
This is why modern microprocessors have a mechanism called branch prediction. A branch predictor attempts to guess whether the jump is taken or not. Then the instruction that is most likely will be speculatively executed beforehand. Once the conditional jump is reached, the condition is checked and if it is guessed right, the program continues with the executed statements. If the guess is wrong, executed statements are discarded and the pipeline starts over with the correct branch by losing some time.
Branch predictors achieve this by keeping a track of the executed conditions. So at first, there is really nothing much to make a guess about. In time, they get better at guessing as there is more historical data available at will. The success rate of the predictor affects your program’s efficiency and in a limited resource environment, branching can be more costly than you could have thought.
If you read this far, you should have noticed that every entry in this list concerns very simple concepts that you learned in the first months of becoming a software engineer: primitive types, if statements, for loops… So, you should never underestimate your enemy.
Congratulations, you are already a better developer than you were yesterday. And I have an hour left to spare. Netflix and chill?
Level Up Coding
Thanks for being a part of our community! Before you go:
- 👏 Clap for the story and follow the author 👉
- 📰 View more content in the Level Up Coding publication
- 🔔 Follow us: Twitter | LinkedIn | Newsletter
🚀👉 Join the Level Up talent collective and find an amazing job
5 Underlying Mechanisms Every Computer Scientist Should Learn was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Can Bayar
Can Bayar | Sciencx (2022-11-20T21:31:10+00:00) 5 Underlying Mechanisms Every Computer Scientist Should Learn. Retrieved from https://www.scien.cx/2022/11/20/5-underlying-mechanisms-every-computer-scientist-should-learn/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
