This content originally appeared on Level Up Coding - Medium and was authored by AlishaAS

Introduction
Python programming has become extremely popular in the past few years. It has made complex tasks fairly easier to accomplish. A reason behind its fast-growing demand is the fact that it is easy to learn and implement than most other programming languages.
The popularity of Python programming can be hugely attributed to the multiple libraries that add in-built functionalities to this versatile programming language. One such library in Python programming is NumPy. NumPy is a library used to do complex mathematical operations in Python.
Let us take a look at it in detail in the next section. Along with this, let us also try to tackle correlation which is one such mathematical operation using NumPy in Python in further sections.
What is NumPy in Python?
Python was not developed with the main motive of performing scientific computations. In earlier times, an array-computing package was designed by a team comprising Python programmer Guido van Rossum. Rossum extended the package to include Python programming syntax.
This is how scientific computing and Python programming found a convergence for the first time. With time, Python has evolved into a leading tool for driving complex scientific mathematical computations.
Such an advancement in the field of Python programming has been made possible with the help of multiple libraries that provide support for carrying out complex mathematical computations with ease.
NumPy is one such library that is supported by the Python programming language. NumPy was developed by Travis Oliphant as part of the SciPy project.
NumPy is used for working with multi-dimensional matrices or arrays as well as performing complex mathematical operations on them. Some of the major features of NumPy can be listed as follows:
- NumPy is fast and easy to use and learn due to its simplified and readable syntax.
- NumPy support is immensely efficient for performing multidimensional array computations with ease.
- NumPy comes with extremely powerful numerical computing tools, such as highly complex mathematical functions, random number generation, Fourier transforms, linear algebra routines, etc.
- NumPy is interoperable, which is to say that it is compatible with a wide range of hardware options and can function well across multiple computing platforms.
- NumPy is an open-source tool that makes it easily accessible to everyone out there.
NumPy can be used to do complex tasks, but this, however, does not mean it cannot also be used to do simpler tasks as well.
Let us take a look at some such examples to better understand how NumPy can be implemented with Python programming.
Example 1: Basic Array Generation
Code:
>>> import numpy as np
>>> arr = np.array([1, 2, 3, 4, 5])
>>> print(arr)
Output:
[1, 2, 3, 4, 5]
Explanation:
- NumPy was imported under the alias “np”
- Then “array()” method was used for creating a one-dimensional array named “arr” containing 5 numbers.
Example 2: Generating a random integer in the range 0–50
Code:
>>> from numpy import random
>>> num = random.randint(50)
>>> print(num)
Output:
27
Explanation:
- From NumPy library, “random” module is imported.
- Then, “randint()” method is used to generate a random integer in the range between 0 to 50 and this integer is stored in a variable num which is later printed.
What is Correlation?
Correlation is a statistic that is used to quantify how two variables relate to each other, such as, how they are linearly associated.
Correlation is an important quantity to make predictions as it explores the relationship between two entities.
One way to calculate the correlation between two variables is with the help of Pearson’s Correlation Coefficient (represented as “r”).
The numerical value of this coefficient (r) lies between -1 and 1. Depending on this value, one can infer how the respective variables correlate.
If the value is
- -1, it represents the perfectly negative correlation between the variables
- Between -1 and 0, it represents a negative correlation between the variables
- 0, it represents no correlation between the variables
- Between 0 and 1, it represents a positive correlation between the variables
- 1, it represents a perfectly positive correlation between the variables.
When the moves farther away from 0 towards -1 or 1, a stronger relationship is represented between the variables.
We can use a scatter diagram to determine the correlation between two variables as well.
For reference, positive, negative, and no correlation might be represented as follows when using scatter diagrams to plot relationships between two variables.
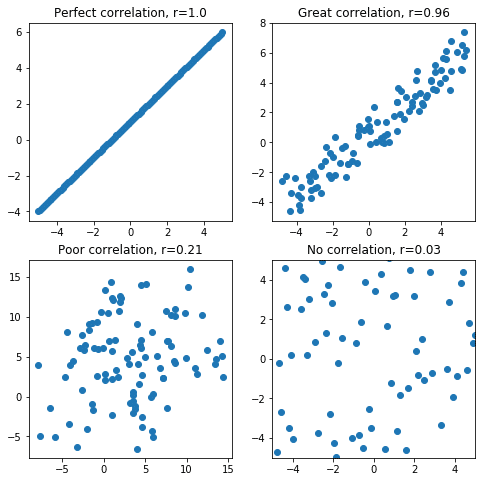
Let us take a closer look at how correlation works with the help of the NumPy library in Python.
What is a Correlation Matrix?
A correlation matrix is a tabular representation of correlation coefficient values between different variables. Each cell in a correlation matrix contains the correlation derived between two variables.
A correlation matrix is also termed a variance-covariance matrix, auto-covariance matrix, or dispersion matrix. Let us take a look at an example of a correlation matrix. In the following correlation matrix, we will explore the correlation between three variables:
- Hours spent studying (H),
- Hours spent sleeping (S), and,
- Marks obtained (M), for a set of students.
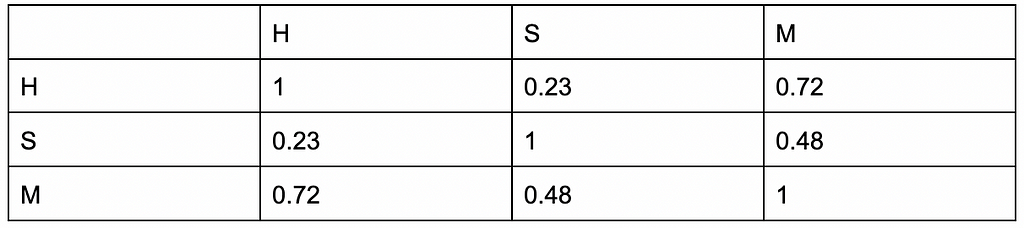
From the above correlation matrix, one can deduce:
- The correlation between Hours spent studying(H) and Hours spent sleeping(S) is 0.23 which shows that the two are not that closely related or linked as compared to how other variables are related. They do not affect each other much, although they might slightly do so as it’s a weakly positive correlation.
- The correlation coefficient between Hours spent studying(H) and Marks obtained(M) is 0.72 which shows a stronger positive correlation than that between other variables. This implies that they are, in fact, closely linked or related to each other. Since the value is positive, an increase in one represents an increase in the other.
- The correlation coefficient between Hours spent sleeping(S) and Marks obtained(M) is more positive than that between H and S but less than that between H and M.
- This implies that S and M affect each other but not as strongly as H affects M (and vice versa) and still stronger than how H affects S (and vice versa). The value is positive implies that an increase in hours spent sleeping leads to an increase in marks obtained too, but still less than how an increase in hours spent studying can increase marks obtained.
How to Create a Correlation Matrix using NumPy in Python?
The major steps involved in creating a correlation matrix with the help of the NumPy library in Python programming can be listed as follows:
- First of all, we would need to import the required libraries. For the sake of this example, we would import the NumPy library. There are also some other libraries in Python that can be used for computing correlation matrices, such as pandas. However, in this article, we will only work with NumPy examples.
- Next, we would need to define the two arrays that would contain the data of the variables between which correlation is to be computed.
- With the help of corrcoef() method in NumPy, we would extract the final correlation matrix between the variables defined in step 2.
Let us now take a look at relevant examples for calculating the correlation matrix using the NumPy library as part of Python programming.
Example 1: Let us create a correlation matrix for the relationship between the length of hair (in cm) and the quantity of shampoo used every month (in mL)
Steps involved:
1- First, we would import the necessary libraries to perform the required operations. Here, NumPy is imported with the help of the following command:
import numpy as np
2- Next, let us define the two array variables as L for storing the data for the length of hair in cm and S for storing the data for how much shampoo is used every month in mL. We can do so using the following command:
- L = [10, 12, 15, 20, 14, 28, 49, 35, 16, 27, 40]
- S = [30, 36, 33, 41, 34, 50, 75, 63, 36, 43, 73]
3- Finally, we will use the corrcoef() method to get the correlation matrix for the correlation existing between variables L and S as defined above. This can be done using:
- corr_mat = np.corrcoef(L, S)
4. Print the resultant matrix obtained using the command:
print(corr_mat)
Completed Code:
import numpy as np
L = [10, 12, 20, 14, 28, 49, 35, 16, 27, 40]
S = [30, 36, 41, 34, 50, 75, 63, 36, 43, 73]
corr_mat = np.corrcoef(L, S)
print(corr_mat)
Output:
[[1. 0.97364586]
[0.97364586 1. ]]
Explanation:
In this case, we can see the correlation matrix above with a very high positive correlation coefficient value (~0.97) between the variables L and S. It denotes that with an increase in L or the length of hair, there is also an increase in S or the amount of shampoo used per month.
Example 2: Let us find the correlation matrix between two random vectors generated using NumPy library’s “random” module
Steps Involved:
1.Firstly, as before, we will simply import NumPy using “np” as alias. This is the most standard way of importing NumPy. One could change the alias used if desired; however, using “np” is recommended. The command is as follows:
import numpy as np
2. Next, we would need to define the two variables to be compared. In this case, the variables are two randomly generated vectors (vect_a and vect_b) that are negatively correlated. Here is the statement we can write to achieve the same:
- vect_a = np.random.randint(0, 100, 500)
- vect_b = (100- vect_a) + np.random.randint(0, 50, 500)
3. Then, we would determine the correlation matrix between “vect_a” and “vect_b” using “corrcoef()” method. The command for the same is as follows:
- corr_mat = np.corrcoef(vect_a, vect_b)
4. Lastly, we will print the result obtained in the previous step using “print” command in Python programming.
print(corr_mat)
Completed Code:
import numpy as np
vect_a = np.random.randint(0, 100, 500)
vect_b = (100- vect_a) + np.random.randint(0, 50, 500)
corr_mat = np.corrcoef(vect_a, vect_b)
print(corr_mat)
Output:
[[ 1. -0.89891262]
[-0.89891262 1. ]]
Explanation:
Here, the resultant correlation coefficient obtained (~ -0.899) is negative. This implies that the two vectors (vect_a and vect_b) generated randomly are negatively correlated.
This simply indicates that a decrease in the value of vect_a might lead to an increase in the value of vect_b. As the value is quite close to -1, it denotes a strong relationship or correlation between the two variables.
Conclusion
In this article, we took a look at how fundamental Python programming has become for scientific computing applications. We studied how Python programming evolved into being the go-to programming language for complex mathematical operations such as multidimensional matrix computations.
Along with this, we also learned about the NumPy library used in Python programming that is widely used for tackling such computations. More specifically, we explored the fundamentals of statistical operation correlation and learned about correlation matrices in detail.
Finally, we implemented what we learned about correlation with the help of NumPy along with Python programming. At multiple points, we studied relevant examples to understand NumPy Correlation in Python programming more comprehensively.
The purpose of this article has been to provide a brief introduction to how Python programming has set the tone for accomplishing difficult mathematical tasks with ease. Studying NumPy is similar to studying many other libraries that are supported by Python.
Thus, one can easily get acquainted with various other libraries to perform the same task of a computing correlation matrix or some other tasks as well. This brings us to the end of the article.
Happy Programming!
Level Up Coding
Thanks for being a part of our community! Before you go:
- 👏 Clap for the story and follow the author 👉
- 📰 View more content in the Level Up Coding publication
- 🔔 Follow us: Twitter | LinkedIn | Newsletter
🚀👉 Join the Level Up talent collective and find an amazing job
What is NumPy Correlation in Python & How to Create a Correlation Matrix? was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by AlishaAS
AlishaAS | Sciencx (2022-11-23T02:31:52+00:00) What is NumPy Correlation in Python & How to Create a Correlation Matrix?. Retrieved from https://www.scien.cx/2022/11/23/what-is-numpy-correlation-in-python-how-to-create-a-correlation-matrix/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
