This content originally appeared on Level Up Coding - Medium and was authored by Arslan Ahmad
Coding patterns enhance our “ability to map a new problem to an already known problem.”

Learning problem-solving using algorithmic patterns was really a life safer for me.
The idea behind these patterns is that once you’re familiar with a pattern, you’ll be able to solve dozens of problems with it.
By doing this, I saved a lot of time I would have otherwise spent preparing for coding interviews.
Today, let’s discuss one of the most frequently used algorithmic patterns called the Island Pattern.
Background
Many coding interview problems involve traversing 2D arrays (aka matrix or grid). The Island pattern describes an efficient way to traverse a matrix. This pattern helps us understand matrix traversal using Depth First Search (DFS) and Breadth First Search (BFS) approaches and their variants.
Let’s jump onto a problem to develop an understanding of this pattern.
For a detailed discussion of these patterns and related problems with solutions, take a look at Grokking the Coding Interview.
Number of Islands (easy)
Problem Statement
Given a 2D array (i.e., a matrix) containing only 1s (land) and 0s (water), count the number of islands in it.
An island is a connected set of 1s (land) and is surrounded by either an edge or 0s (water). Each cell is considered connected to other cells horizontally or vertically (not diagonally).
Example 1
Input: matrix =
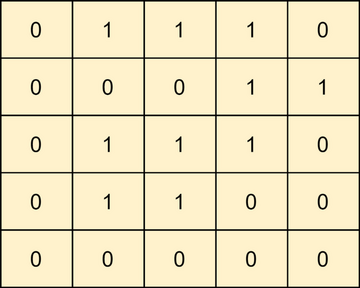
Output: 1
Explanation: The matrix has only one island. See the highlighted cells below.
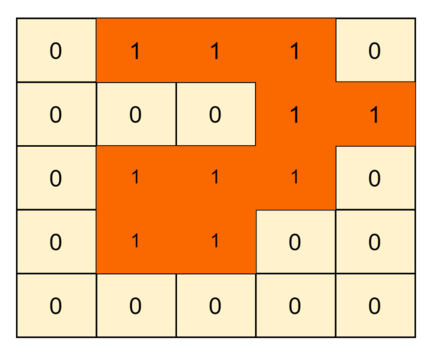
Example 2
Input: matrix =
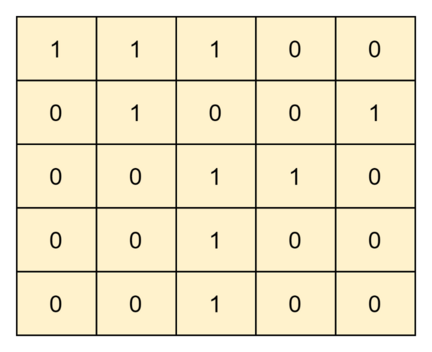
Output: 3
Explanation: The matrix has three islands. See the highlighted cells below.
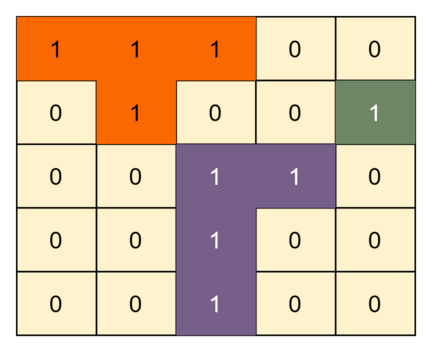
Solution
We can traverse the matrix linearly to find islands.
Whenever we find a cell with the value ‘1’ (i.e., land), we have found an island. Using that cell as the root node, we will perform a Depth First Search (DFS) or Breadth First Search (BFS) to find all of its connected land cells. During our DFS or BFS traversal, we will find and mark all the horizontally and vertically connected land cells.
We need to have a mechanism to mark each land cell to ensure that each land cell is visited only once. To mark a cell visited, we have two options:
- We can update the given input matrix. Whenever we see a ‘1’, we will make it ‘0’.
- A separate boolean matrix can be used to record whether or not each cell has been visited.
Following is the DFS or BFS traversal of the example-2 mentioned above:
By following the above algorithm, every time DFS or BFS is triggered, we are sure that we have found an island. We will keep a running count to calculate the total number of islands.
Bellow, we will see three solutions based on:
- DFS
- BFS
- BFS with visited matrix
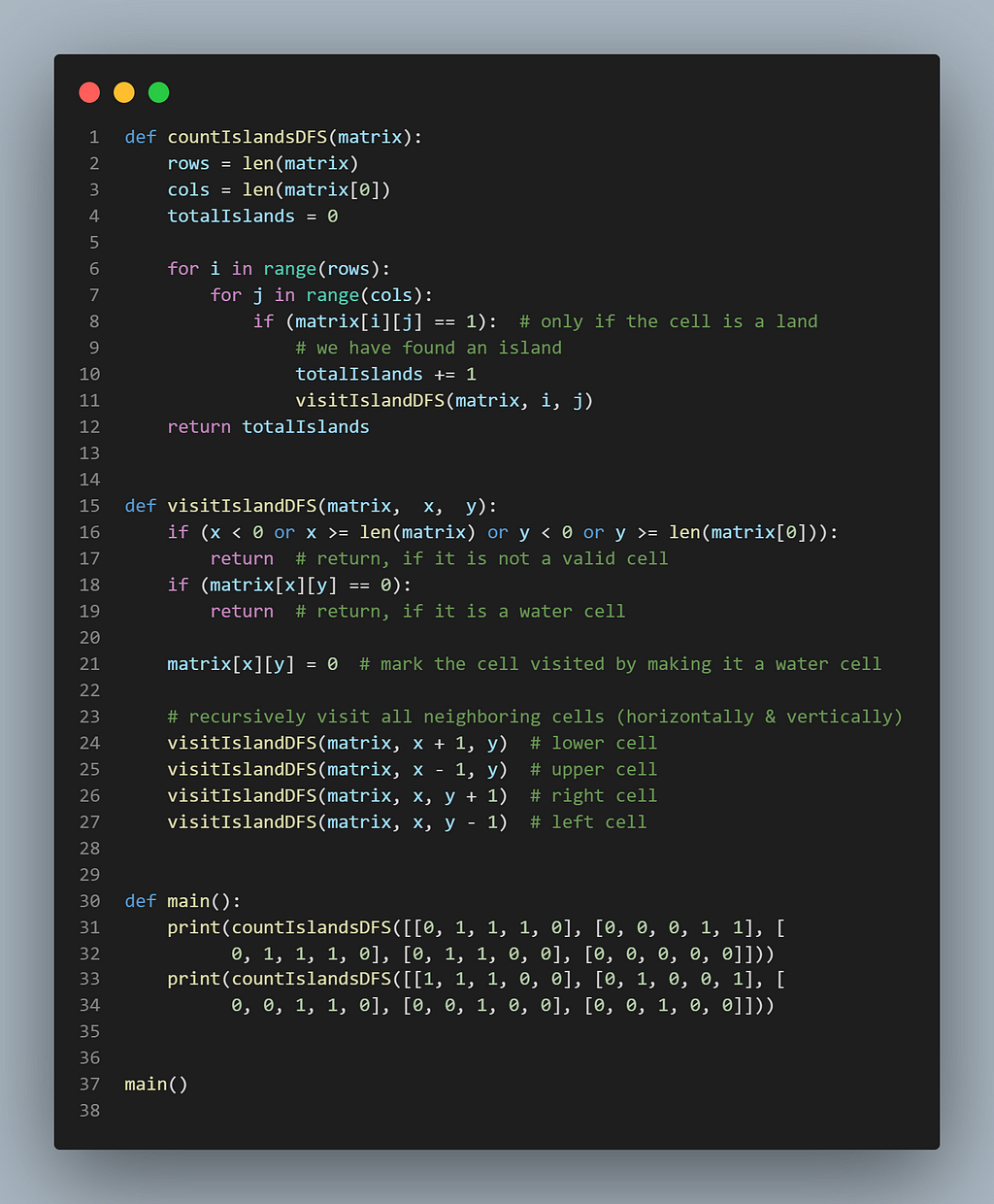
Code (DFS)
Here is what our DFS algorithm will look like. We will update the input matrix to mark cells visited.
Time Complexity
The time complexity of the above algorithm will be O(M*N), where ‘M’ is the number of rows and ’N’ is the number of columns of the input matrix. This is due to the fact that we have to traverse the whole matrix to find the islands.
Space Complexity
DFS recursion stack can go M*N deep when the whole matrix is filled with ‘1’s. Hence, the space complexity will be O(M*N), where ‘M’ is the number of rows and ’N’ is the number of columns of the input matrix.
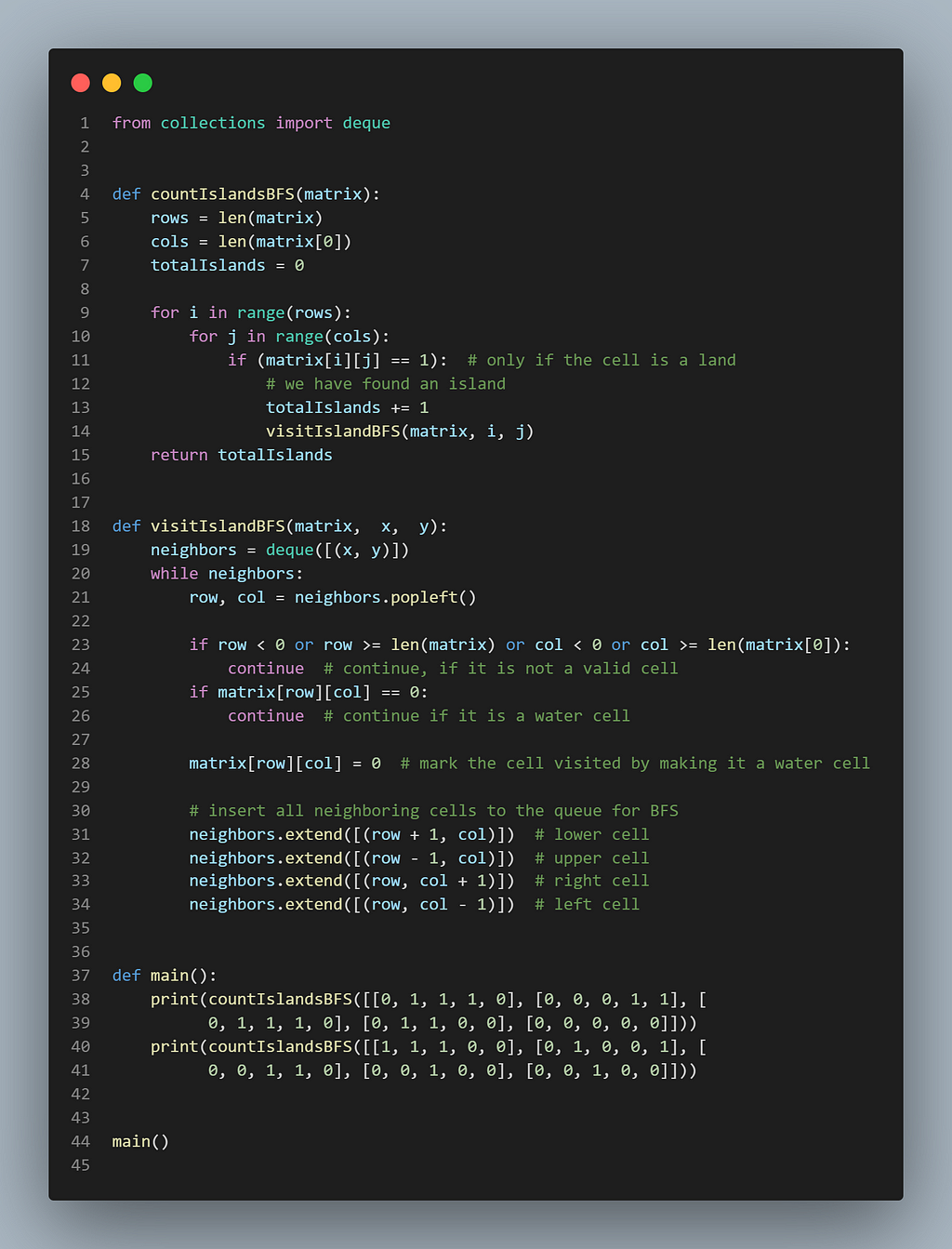
Code (BFS)
Here is what our BFS algorithm will look like. We will update the input matrix to mark cells visited.
Time Complexity
Time complexity of the above algorithm will be O(M*N), where ‘M’ is the number of rows and ’N’ is the number of columns.
Space Complexity
Space complexity of the above algorithm will be O(min(M,N). In the worst case, when the matrix is completely filled with land cells, the size of the queue can grow up to min(M,N).
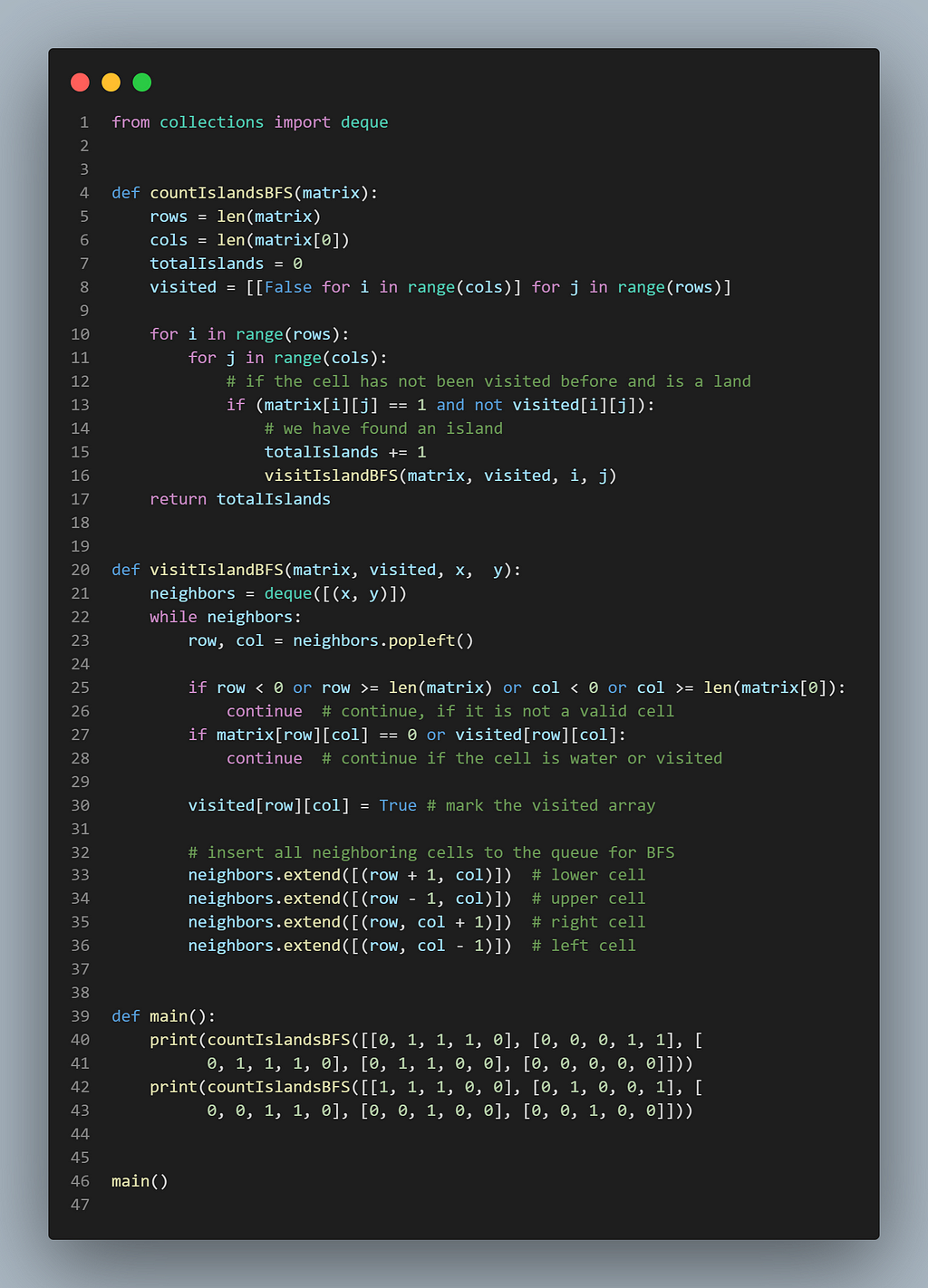
Code (BFS with visited matrix)
Here is what our DFS algorithm will look like. We will keep a separate boolean matrix to record whether or not each cell has been visited.
Time Complexity
Time complexity of the above algorithm will be O(M*N), where ‘M’ is the number of rows and ’N’ is the number of columns.
Space Complexity
Because of the visited array and max size of the queue, the space complexity will be O(M*N), where ‘M’ is the number of rows and ’N’ is the number of columns of the input matrix.
Other Problems Based on the Island Pattern
Here are a few more problems that can be solved using the Island pattern:
- Biggest Island (easy)
- Flood Fill (easy)
- Number of Closed Islands (easy)Island Perimeter (easy)
- Number of Distinct Islands (medium)
- Cycle in a Matrix (medium)
Conclusion
Like it or not, LeetCode-type questions are part of almost every programming interview, so every software developer should practice them before an interview. Their only option is to prepare smartly and learn problem-solving by focusing on the underlying problem patterns. Learn more about these patterns and sample problems in Grokking the Coding Interview and Grokking Dynamic Programming for Coding Interviews .
Check Design Gurus for some interesting courses on Coding and System Design interviews.
- Don't Just LeetCode; Follow the Coding Patterns Instead
- Top LeetCode Patterns for FAANG Coding Interviews
Grokking the Coding Interview: Pattern Island was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Arslan Ahmad
Arslan Ahmad | Sciencx (2022-12-01T03:05:21+00:00) Grokking the Coding Interview: Pattern Island. Retrieved from https://www.scien.cx/2022/12/01/grokking-the-coding-interview-pattern-island/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
