Implement an External Memory Merge Sort Algorithm

This content originally appeared on Level Up Coding - Medium and was authored by Chris Bao

Introduction

This article will examine one interesting question which I came across when reading the book Programming Pearls. This question simply goes like this: How to sort a large disk file? The disk file has so much data that it cannot all fit into the main memory. I considered this algorithm question for a while; but noticed that all the classic sorting algorithms, like Quick sort and merge sort, can’t solve it easily. Then I did some research about it, and I will share what I learned in this article. I believe you can solve this problem as well, after reading this article.

Background of External Algorithm

Traditionally, computer scientists analyze the running time of an algorithm by counting the number of executed instructions, which is usually expressed as a function of the input size n, like the well-known Big O notation. This kind of algorithm complexity analysis is based on the Random access machine(RAM) model, which defines the following assumptions:

• A machine with an unbounded amount of available memory;
• Any desired memory location can be accessed in unit time;
• Every instruction takes the same amount of time.

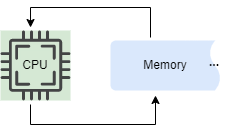
This model works well when the amount of memory that the algorithm needs to use is smaller than the amount of memory in the computer running the code.

But in the real world, some applications need to process data that are too large to fit into a computer’s main memory at once. And the algorithms used to solve such problems are called external memory algorithms or disk-based algorithms; since the input data are stored on an external memory storage device.

Instead of the RAM model, the external memory algorithm is analyzed based on the external memory model. The model consists of a CPU processor with an internal memory of bounded size, connected to an unbounded external memory. One I/O operation consists of moving a block of contiguous elements from external to internal memory(this is called page cache and is managed by the kernel.).

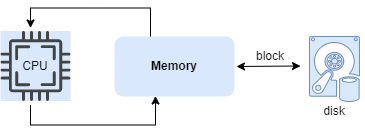
Compared with the main memory, the access speed of external memory is slower by several orders of magnitude, even though modern storage techniques such as SSD are already adopted. Thus, for external algorithms, the bottleneck of the performance is disk IO speed instead of the CPU cycles.

In this section, we examined the computational model of the external memory algorithms. Next, let’s review one typical type of external memory algorithm: external sorting.

External Mergesort

Similar to the traditional internal sorting algorithms, several different solutions are available for external sorting. In this article, I will focus on external mergesort.

External mergesort is a straightforward generalization of internal mergesort. The algorithm starts by repeatedly loading M input items into the memory(since the memory buffer size is limited, can only store M input items at once), sorting them, and writing them back out to disk. This step divides the input file into some(or many, if the input file is very large) sorted runs, each with M items sorted. Then the algorithm repeatedly merges multiple sorted runs, until only a single sorted run containing all the input data remains.

Let’s use the following example model to analyze this algorithm. First of all, assume the memory buffer is limited, and the size is one page. And the input file size is 8 pages. External mergesort can be divided into two phases: sort phase and merge phase.

Sort phase:

• Divide the entire input file into 8 groups, each group size is one page(memory buffer capacity).
• Load each page into the memory, sort the items in the memory buffer(with an internal sorting algorithm), and save the sorted items in a temporary sub-file. Each sub-file is called a run.

At the end of the sort phase, 8 temporary sorted 1-page runs will be created. This step can be marked as pass 0.

Merge phase:

The 8 sorted runs in pass 0 will be merged into a single sorted file with 3 more passes.

pass 1: Perform 4 runs for the merge.

• Run 1: Merge the first two small 1-page runs into a big 2-page run. This merging step goes as follows:
• Read the first two sorted sub-files (one item from each file).
• Find the smaller item, output it in the new sub-file, and the appropriate input sub-file is advanced. Repeat this cycle until the input sub-file is completed. This routine’s logic is the same as the internal mergesort algorithm.
• Run 2: Merge the next two 1-page runs into a 2-page run.
• Run 3 and 4: follow the same process.
• At the end of pass 1, 4 temporary sorted 2-page runs will be created.

pass 2: Perform 2 runs for the merge.

• At the end of pass 2, 2 temporary sorted 4-page runs will be created.

pass 3: Perform 1 run for the merge.

• At the end of pass 3, the final 8-page run containing all the sorted items will be created.

Note: the above process may seem complicated at the first sight, but the logic is nearly the same as the internal merge sort. The only difference is internal merging is based on memory buffers, while external merging is based on disk files, and needs reading the item from disk to memory.

Since we keep merging two small sub-files into a big one with doubled size, the above algorithm can be called two-way external merge sorting. We can generalize the idea to multi-way external merge sorting, which merges M runs into one.

Next, let’s analyze its complexity. Suppose the input file has N items and each page consists of B items. And M denotes the number of ways used in the merge phase, thus the number of passes should be: logM(N/B) + 1, where plus one means the first pass in the sort phase. And each pass, each item is read and written once from and to the disk file. So the total number of disk I/O is: 2N*(logM(N/B) + 1)

In this section, we examined the abstract computational model of the external memory algorithm and analyzed the details of the external mergesort algorithm. Next section, let’s implement the code and evaluate the performance.

First, you can find all the source codes of this implementation in this Github repo.

GitHub - baoqger/external-merge-sort: external-sort

In this repo, I implemented both two-way and multi-way solutions, which are tracked in different branches, please be aware of this. But for the sake of simplicity, I will focus on the generalized multi-way mergesort solution in this article.

Data Preparation

Before diving into the code, let’s define the problem we need to solve here. I will generate an input file containing several millions of seven digits random numbers, from 1,000,000 to 9,999,999. The random numbers can be duplicated, and each number is stored in one new line of the input file. The input file is prepared with the following Bash script which calls GNU shuf :

#!/usr/bin/bash 

# Author: Chris Bao
# Generate millions of seven digits random integers
# based on shuf utility

shuf -i 1000000-9999999 -n 7777777 > ./input.txt

The generated input file is roughly 60 MB in size. For modern computers, it can be loaded to memory easily. But since we are working external memory algorithm, so let’s assume we are running the algorithm on an old computer, which has only 100000 Byte memory. Based on this assumed restriction, we need to sort the numbers in the input file and save the result in a new file.

Implementation

Let’s define some global constants in this algorithm:

#ifndef CONSTANT_H
#define CONSTANT_H

#define MEMORY_LIMIT 100000
#define RECORD_SIZE 4
#define MULTI_WAY_NUMBER 2

#endif

MEMORY_LIMIT denotes the 100000 bytes memory limit; In C, we can use the type unsigned int to store an integer in the range from 1,000,000 to 9,999,999. So RECORD_SIZE means each record(or integer) will take up 4 bytes of memory.

And by default, the algorithm will use the two-way merge, but the user can pass an argument to run a multi-way merge too.

Sort phase

The sort phase is implemented inside the separationSort function as follows:

/*
 * Goes through a given file and separates that file into sorted 1MB files using (internal) mergeSort algorithm
 * */
void separationSort(FILE *input) {
    FILE *fp;
    unsigned int *buffer = malloc(sizeof(unsigned int)*(MEMORY_LIMIT/RECORD_SIZE));
    char *line = NULL;
    size_t len = 0;
    ssize_t nread;
    int count = 0;
    printf("Sort phase start.\n");
    while((nread = getline(&line, &len, input)) != -1) {
        if (count < MEMORY_LIMIT/RECORD_SIZE) {
            buffer[count++] = (unsigned int)strtoul(line, NULL, 10); 
        } else {
            mergeSort(buffer, count); // sort records
            
            // output sorted to file
            if (fileNum == 1) { // create the dir
                int status;
                // create tmp directory
                if ((status = mkdir("./tmp", S_IRWXU | S_IRWXU | S_IROTH | S_IXOTH)) == -1) {
                    fprintf(stderr, "Failed to create tmp directory.\n");
                    exit(EXIT_FAILURE);
                }
                // create pass0 directory for sort phase
                if ((status = mkdir("./tmp/pass0", S_IRWXU | S_IRWXU | S_IROTH | S_IXOTH)) == -1) {
                    fprintf(stderr, "Failed to create pass0 directory.\n");
                    exit(EXIT_FAILURE);
                }
 
            }

            char fileName[20];
            sprintf(fileName, "./tmp/pass0/%d.txt", fileNum);
            if ((fp = fopen(fileName, "w+")) == NULL) {
                fprintf(stderr, "Failed to create file: %s.\n", fileName);
                exit(EXIT_FAILURE);
            }

            outputToFile(buffer, count, fp);

            // Reset memory buffer(zero-out the entire array)
            memset(buffer, 0, sizeof(unsigned int)*(MEMORY_LIMIT/RECORD_SIZE));
            count = 0;
            fileNum++;
            buffer[count++] = (unsigned int)strtoul(line, NULL, 10); // add the current record into new buffer's as first element
            
        }
    }

    // sort the last and final file
    mergeSort(buffer, count);
    char fileName[20];
    sprintf(fileName, "./tmp/pass0/%d.txt", fileNum);
    if ((fp = fopen(fileName, "w+")) == NULL) {
        fprintf(stderr, "Failed to create file: %s.\n", fileName);
        exit(EXIT_FAILURE);
    }
    outputToFile(buffer, count, fp);
    
    free(buffer);
    free(line);
    printf("Sort phase done. %d tmp sorted files are produced.\n", fileNum);
}

The logic is not difficult. The function takes the input file descriptor as a parameter and reads each line(via the getline method) in a loop until reaches the end of the file. The numbers will be read into the memory buffer before hitting the memory limit. When the memory buffer is full(100000 bytes), the numbers are sorted with the function mergeSort.

The function mergeSort is defined inside the file internal_sort.c, which implements the classic internal merge sorting algorithm. I will not cover it in this article, since you can find many documents about it online. If you don’t know about it, please spend some time learning about it. Of course, you can replace it with other sorting algorithms like quick sort too. I leave this for the readers.

After sorting, the numbers are saved in the temporary files in the directory of ./tmp/pass0. The filename is just the run number.

/*
 * Output sorted record to given file(of)
 * */

void outputToFile(unsigned int *buffer, int size, FILE *of) {
    int i;
    for (i = 0; i < size; i++) {
        fprintf(of, "%u\n", buffer[i]);
    }
    fclose(of);
}

We can verify the result of the sort phase as follows:

You can see each file contains up to 25000 (equal to MEMORY_LIMIT/RECORD_SIZE) numbers and 312 files are created in pass0.

Note that I will not examine the details about how to make a new directory and how to open a new file to read or write. You can learn such Linux file I/O concepts by yourself.

Merge phase

The exMerge function controls the passes in the merge phase starting from pass1.

void exMerge() {
    /* some code omitted ... */
    int pass = 1;
    while (fileNum > 1) {
        exMergeSort(pass, fileNum);
        int remainer = fileNum % ways;
        fileNum = fileNum / ways;
        if (remainer > 0) {
            fileNum++;
        } 
        pass++;
    }
    /* some code omitted ... */
}

The variable fileNum stores the run number in each pass. And the variable ways denotes the number of multi-way. Thus, the run number of the next pass should be calculated as fileNum / ways.

The detailed merging logic is inside the function exMergeSort, which takes two parameters. pass means the current pass number(starting from 1), while nums means how many runs(or sub-files) in the last pass need to be merged.

void exMergeSort(int pass, int nums) {
    /* some code omitted ... */
    int inputFileNum = 0; 
    int run = 1;
    for (; inputFileNum < nums;) { 
        
        // create the dir for current pass
        if (inputFileNum == 0) {
            int status;
            char dirName[20];
            sprintf(dirName, "./tmp/pass%d", pass);
            if ((status = mkdir(dirName, S_IRWXU | S_IRWXU | S_IROTH | S_IXOTH)) == -1) {
                fprintf(stderr, "Failed to create tmp directory %s.\n", dirName);
                exit(EXIT_FAILURE);
            }
        }
        // open new file to merge in each run
        FILE *fm; 
        char mergedFileName[20];
        sprintf(mergedFileName, "./tmp/pass%d/%d.txt", pass, run);
        if ((fm = fopen(mergedFileName, "w+")) == NULL) {
            fprintf(stderr, "%s\n", strerror(errno));
            fprintf(stderr, "merged file %s: can't create or open.\n", mergedFileName);
        }
        run++;
        /* some code omitted ... */
    }

}

The above code creates a temp directory for each pass and a temp file for each run.

Next, we create an array of the input files for each run. And the input file is inside the temp directory of the last pass. Each run merges multiple files in the for loop. The only trick logic here is that the remaining files in the last run may be less than the number of ways declared, we need to handle that properly (line 5 of the below code block).

// Rewind the sorted files in previous pass, each run merge way_numbers numbers of files
// Merge the sorted files with multi ways in N runs. 
// In the first N - 1 runs, each run merge ways numbers of files
// In the last run, merge the remaining files. 
int way_numbers = run * ways <= nums ? ways : nums - inputFileNum;
FILE *fiarr[way_numbers];
for (int i = 0; i < way_numbers; i++) {
   char inputFileName[20];
   inputFileNum++; // start from 0 to nums
   sprintf(inputFileName, "./tmp/pass%d/%d.txt", pass - 1, inputFileNum);
   if ((fiarr[i] = fopen(inputFileName, "r")) == NULL) {
        fprintf(stderr, "%s\n", strerror(errno));
        fprintf(stderr, "input file %s: can't create or open.\n", inputFileName);
   }
   rewind(fiarr[i]);
}

Next, we need to read one number from every input file until only one file is not run out. Find the smallest one and save it in the temp output run file. And for the last remaining file, remember to put the rest numbers into the output file too.

// get and compare records until files runs out of records
char *records[way_numbers]; 
for (int i = 0; i < way_numbers; i++) {
    records[i] = getRecord(fiarr[i]);
}
// loop until only one file is not run-out
while(validateRecords(records, way_numbers )) {
    int index = getMinRecordIndex(records, way_numbers);
    fprintf(fm, "%s", records[index]); // print record to new merged file
    free(records[index]); // free the memory allocated by getline in getRecord function
    records[index] = getRecord(fiarr[index]); // Get new record from the file
}
       
// put the rest record in the last remaining file into new file 
int lastIndex = getLastRemainRecordIndex(records, way_numbers);
while(records[lastIndex]) {
    fprintf(fm, "%s", records[lastIndex]);
    free(records[lastIndex]);
    records[lastIndex] = getRecord(fiarr[lastIndex]);
}

The above code bock utilizes several methods like getRecord, validateRecords, getMinRecordIndex and getLastRemainRecordIndex as follows, and these functions are easy to understand.

/*
 * Returns a copy of the record
 *
 * */
char* getRecord(FILE *ifp) {
    char *line = NULL;
    size_t len = 0;
    ssize_t nread;
    while ((nread = getline(&line, &len, ifp)) != -1) {
        return line;       
    }
    return NULL;
}
/*
 * Validate whether at least two records are non-zero
 * */
bool validateRecords(char **records, int size) {
    int count = 0;
    for (int i = 0; i < size; i++) {
        if (records[i] != NULL) {
            count++;
        }
    }
    return count >= 2;
}

/*
 * Get the min valid record's index
 * */
int getMinRecordIndex(char **records, int size) {
    int index = 0;
    unsigned int min = (int)INFINITY;
    for (int i = 0; i < size; i++) {
        if (records[i] == NULL) { // pass invalid run-out record files
            continue;
        } 
        if (strtoul(records[i], NULL, 10) < min) {
            min = strtoul(records[i], NULL, 10);
            index = i;
        }
    }
    return index;
}
/*
 * Get the last remainer of the records
 * */
int getLastRemainRecordIndex(char **records, int size) {
    for (int i = 0; i < size; i++) {
        if (records[i] != NULL) {
            return i;
        }
    }
}

In detail, you can refer to the source code of this github repo. Next, let’s evaluate the performance of this algorithm by tuning the number of ways for merging.

Performance Evaluation

We’ll use the Linux time utility to measure the running time of this algorithm.

The result of two-way mergesort is:

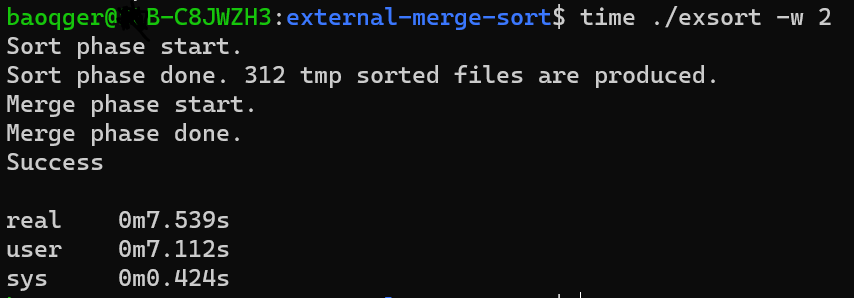
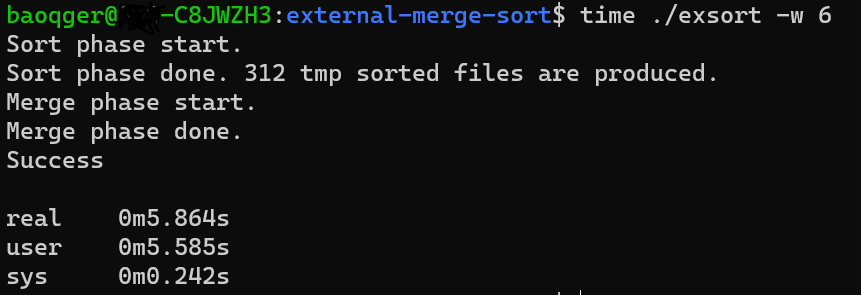
while six-way mergesort can complete with a shorter runtime.

Summary

In this article, we examine how an external merge sort algorithm works by implementing one from scratch.

Implement an External Memory Merge Sort Algorithm was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.

This content originally appeared on Level Up Coding - Medium and was authored by Chris Bao

Print Share Comment Cite Upload Translate Updates

APA

Chris Bao | Sciencx (2022-12-08T03:51:23+00:00) Implement an External Memory Merge Sort Algorithm. Retrieved from https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/

MLA

" » Implement an External Memory Merge Sort Algorithm." Chris Bao | Sciencx - Thursday December 8, 2022, https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/

HARVARD

Chris Bao | Sciencx Thursday December 8, 2022 » Implement an External Memory Merge Sort Algorithm., viewed ,<https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/>

VANCOUVER

Chris Bao | Sciencx - » Implement an External Memory Merge Sort Algorithm. [Internet]. [Accessed ]. Available from: https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/

CHICAGO

" » Implement an External Memory Merge Sort Algorithm." Chris Bao | Sciencx - Accessed . https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/

IEEE

" » Implement an External Memory Merge Sort Algorithm." Chris Bao | Sciencx [Online]. Available: https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/. [Accessed: ]

rf:citation

» Implement an External Memory Merge Sort Algorithm | Chris Bao | Sciencx | https://www.scien.cx/2022/12/08/implement-an-external-memory-merge-sort-algorithm/ |

Please log in to upload a file.

There are no updates yet.
Click the Upload button above to add an update.

You must be logged in to translate posts. Please log in or register.