This content originally appeared on Brave's latest news on Brave Browser and was authored by Brave's latest news on Brave Browser

Authors: Sofía Celi, cryptography researcher at Brave; Alex Davidson, former cryptography researcher at Brave; and Gonçalo Pestana, former cryptography researcher at Brave.
One of the interesting problems in computer science with regard to security and privacy is how to retrieve items from a database, without revealing anything about the query to the untrusted server(s) where this database lives. Today, we’re going to be talking about some very recent scientific work we have done at Brave to make this a genuine possibility for a variety of applications.
The TL;DR is that we have built a new Private Information Retrieval (PIR) scheme called FrodoPIR, that we hope will make PIR easier and cheaper to deploy for a variety of use-cases and applications, such as Safe Browsing, checking passwords over breached databases, certificate revocation checks, streaming, and more. We have an open-source implementation that you can use now, as well as a paper that explains the scheme. The paper has been accepted into the first issue of PoPETS 2023! We’re calling the scheme FrodoPIR because the client can perform hidden queries to the server, just as Frodo remained hidden from Sauron.
Private Database Access Overview
Why is the issue of privacy important when retrieving items from a database? Let’s say, for example, that you want to use your favorite streaming platform to watch videos of dogs. But, actually, you’re a little bit embarrassed of revealing — to the platform — how many dog videos you watch (you shouldn’t be, but that’s the world we live in). Moreover, you would love to avoid anyone from being able to exploit that data so they can show you invasive targeted advertising campaigns, for example. What would be great is if you could receive this content, without the (untrusted) provider being able to tell what it is you are streaming.
Private Information Retrieval (PIR) schemes are a set of cryptographic protocols that have been proposed as a solution to this exact problem. As with most cryptography, the first schemes arrived in the 1990’s, but it hasn’t been until the last six or seven years that candidate schemes have been designed that may approach having high enough performance to work in modern-day use-cases. However, the landscape remains quite complicated: many schemes are tailored to very specific use-cases to achieve low bandwidth or server runtimes, or they may require complex server-side deployments (e.g. using at least two non-colluding servers) to fulfill PIR queries.
With this in mind, we created FrodoPIR! This new PIR scheme we are announcing is intensely configurable, efficient across a wide swath of applications, easy to understand and implement, requires only a single untrusted server to deploy, and comes with concrete privacy and security guarantees against both classical and quantum adversaries (because we use lattices, as we will see).
PIR: The General Idea
Broadly speaking, the way that most single-server PIR schemes work is by using a cryptographic tool known as additively homomorphic encryption (AHE). Such encryption schemes allow someone with two ciphertexts that encrypt X and Y to compute a ciphertext that encrypts X+Y, without knowledge of the secret key. Such schemes have been around since RSA, but one commonly-used example is the Paillier encryption scheme.
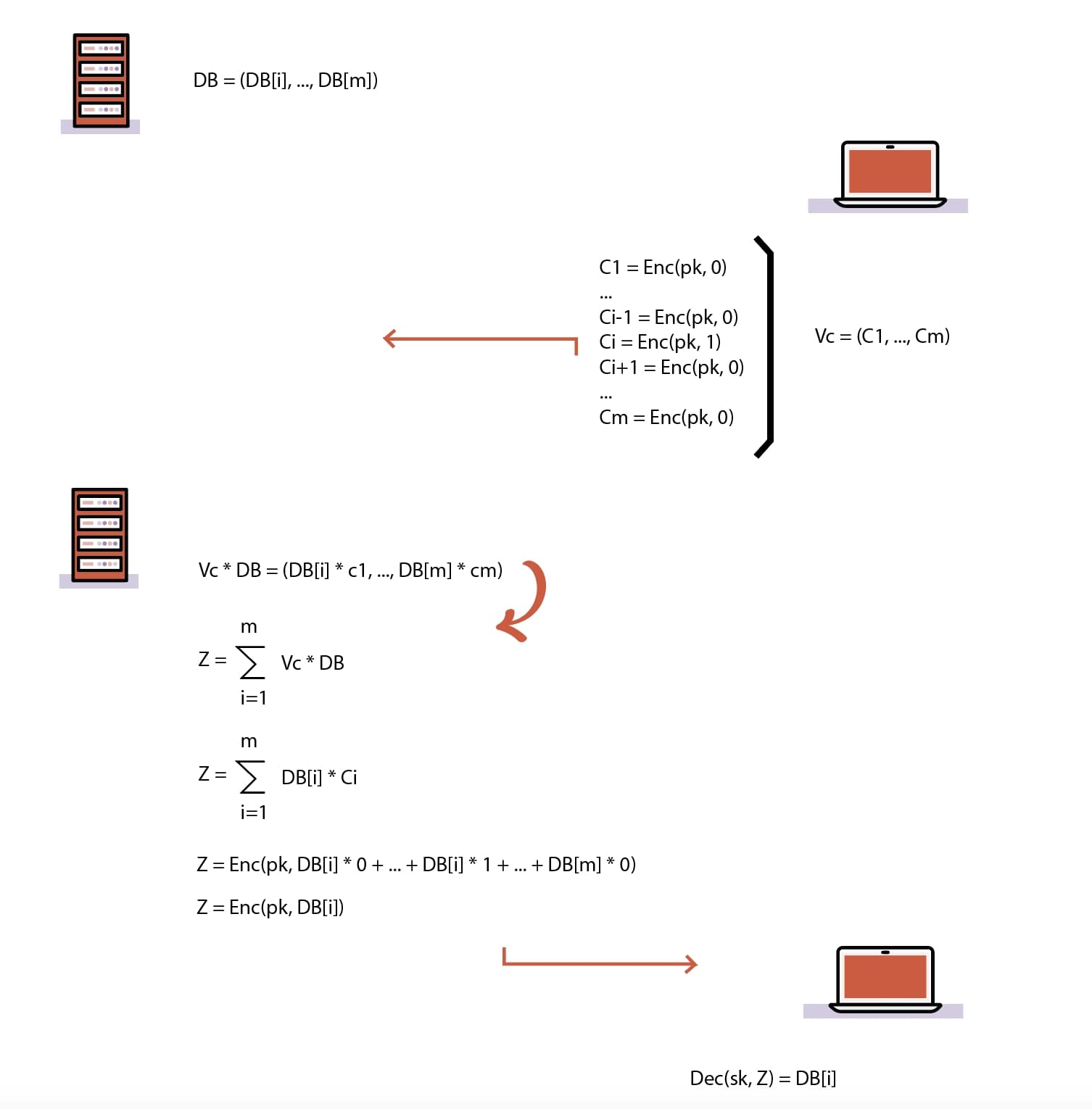
Figure 1: an AHE system
But how do we build a PIR protocol from such a thing? As seen in Figure 1, the answer is remarkably simple:
- The server organizes its database into a set of M rows, each containing a single element. In other words, the database is now a vector.
- Any client that wants to learn the ith element, encrypts M ciphertexts, where the ith ciphertext encrypts 1, and the rest of them encrypt 0.
- The client sends their ciphertexts to the server; due to the nature of the encryption, the server cannot tell what is encrypted.
- The server performs a scalar multiplication of each entry db_entry_1,…,db_entry_M of its database vector with the corresponding ciphertext in each, adds them all together into a single ciphertext and returns this back to the client. Note that scalar multiplications are possible by adding each ciphertext to itself according to the size of the scalar.
- Now, after the client decrypts each ciphertext, it will simply learn db_entry_i, since: 0db_entry_1,…,1db_entry_i,…,0*db_entry_M = db_entry_i.
Essentially, over the past number of years, it has been shown that constructing PIR can be done quite efficiently using this simple method (and some optimizations). This is achieved by using AHE schemes based on cryptographic lattices, in particular based on fully homomorphic encryption (FHE) schemes, with security derived from the ring learning with errors (RLWE) assumption.
We’ll talk about these a bit more shortly. Some things to note before we do:
- It’s possible to construct PIR with multiple servers with higher efficiency, but under the assumption that the servers do not collude. Such assumptions are known to be quite strong in real-world settings, and it is preferred to avoid them, if possible.
- The server are assumed to be honest-but-curious, i.e. they execute the protocol honestly, but attempt to learn more from the client query alone. A malicious server can obviously choose to not run the PIR protocol properly, and clients will get bad answers.
- The server database is assumed to be public. If the database should be treated as sensitive (i.e. clients should not be able to learn anything other than their query), then PIR is not really the correct tool to use (though, there are some symmetric PIR constructions that give insight into this).
Limitations to existing approaches
At Brave, we became interested in using PIR for having clients retrieve certain things from Brave, without the server knowing. Unfortunately, despite experimenting with various existing systems, we were never able to build something that didn’t involve huge costs, or large amounts of implementation complexity. This led us to start thinking about how we could try and build a PIR scheme that fit these requirements a little better and to create a new approach: FrodoPIR. Let’s see now what are the limitations of existing approaches.
A common issue even with fairly recent PIR schemes is that they are expensive in terms of either bandwidth, or in the amount of time taken to process each client query. In order to drive down the costs, FHE-based PIR schemes can move large proportions of the expensive online computation and communication (which is, for example, the sending of the query) to an offline phase (a “preparation” phase that can be later reused to make online queries). These kinds of schemes are called offline-online or stateful, as opposed to online-only or stateless.
However, a key difficulty that has gone unsolved is that either the computation or the communication costs induced during the offline phase scale linearly in the number of clients that will make queries, or the client has to download the entire server database (which defeats the purpose). This means that the offline phase has to be performed between each client and the server, which translates, in principle, to a lot of expensive computation that the server has to do. If you’re using commercial hardware to run your server, these costs are likely to run up huge financial costs.
Announcing FrodoPIR!
Just as the state of Sauron (its ring) moved to Frodo, we can move the mu and A to the client. The client then can then perform hidden queries to the server, just as Frodo remains hidden from Sauron.
We are excited to present FrodoPIR, a stateful PIR scheme that is built directly upon the learning with errors (LWE) problem. We get rid of the ring lattice structures (as Frodo needs to do: a reference first made in the naming of the FrodoKEM proposal, and that we now borrow ourselves) to bring a flexible and practically efficient PIR scheme for a variety of use-cases. The core of the FrodoPIR scheme is an offline phase that requires no client-dependent computation, and incurs only a relatively small download compared to the database size (e.g. 170x smaller). This makes it suitable for many large, real-world deployments, where lowering financial costs for server-side operators is of paramount importance. FrodoPIR is also significantly simpler than previous schemes, making no use of FHE techniques and requiring only modular arithmetic. Read the whole paper describing it here.
FrodoPIR is a scheme that relies on the decisional LWE problem: each client query is a noisy vector that appears uniformly random to the server. As stated, it has both offline and online phases:
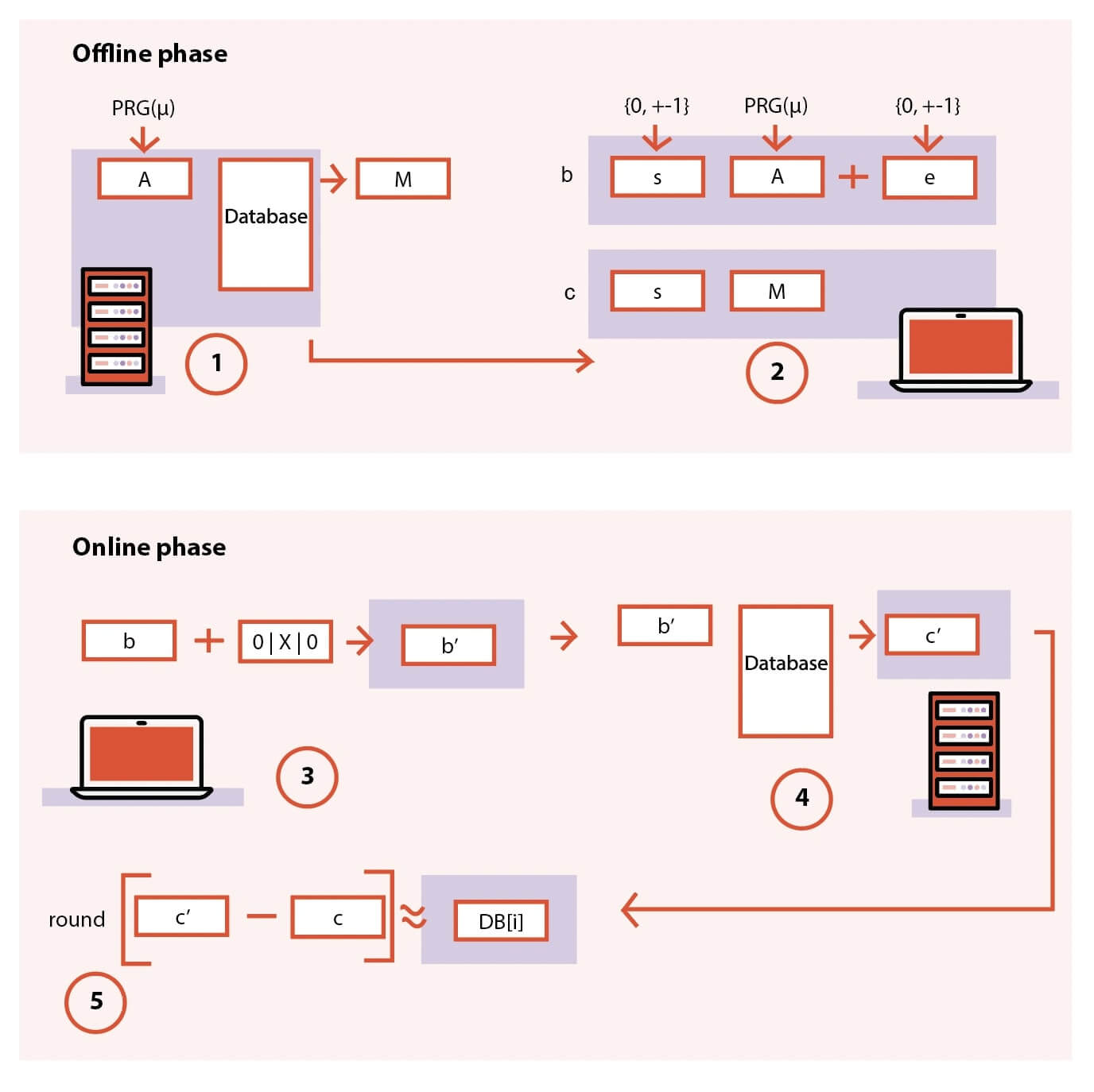
Figure 2: Diagram of the flow of FrodoPIR
- In the offline phase, the server interprets the database as a matrix, applies a compression function to said matrix and makes the results available as global public parameters (mu and M). This compression function shrinks the size of the database.
- In the offline phase, the client downloads the public parameters (mu and M), and computes ‘c’ sets of preprocessed query parameters.
- In the online phase, the client uses a single set of preprocessed query parameters to produce an “encrypted” query vector, which is sent to the server.
- The server responds to the query by multiplying the vector with its database matrix.
- The client returns the result by “decrypting” the response using its preprocessed query parameters.
What this means is that in the offline phase, the server and client prepare anything that can be previously prepared for online queries; and, in the online phase, the client sends encrypted queries to the server. The latter returns a positive or negative value depending if the query is found in the database or not. The server never learns which value you are querying for, and yet it returns the correct answer (if it was included in the database or not).
FrodoPIR is a powerful primitive as it makes PIR schemes practical for real-world usage where not only communicational and computational costs are important but also financial ones. PIRs, in general, are powerful: they can be applied to Safe Browsing, checking passwords over breached databases (or any type of credentials), Certificate Transparency (CT) checks, certificate revocation checks, or for streaming. Having a cheap and efficient scheme will help improve the privacy of the whole Internet not only for big actors, but also for anyone providing such service.
It is worth noting that there are other PIR schemes beyond FrodoPIR, but the latter outperforms them all, as seen in Figure 3 below. The figure shows a comparison of per-client computational, communication, and financial costs for the server when running FrodoPIR, Stateful OnionPIR (SOnionPIR), and PSIR, assuming that each client makes c = 500 queries.
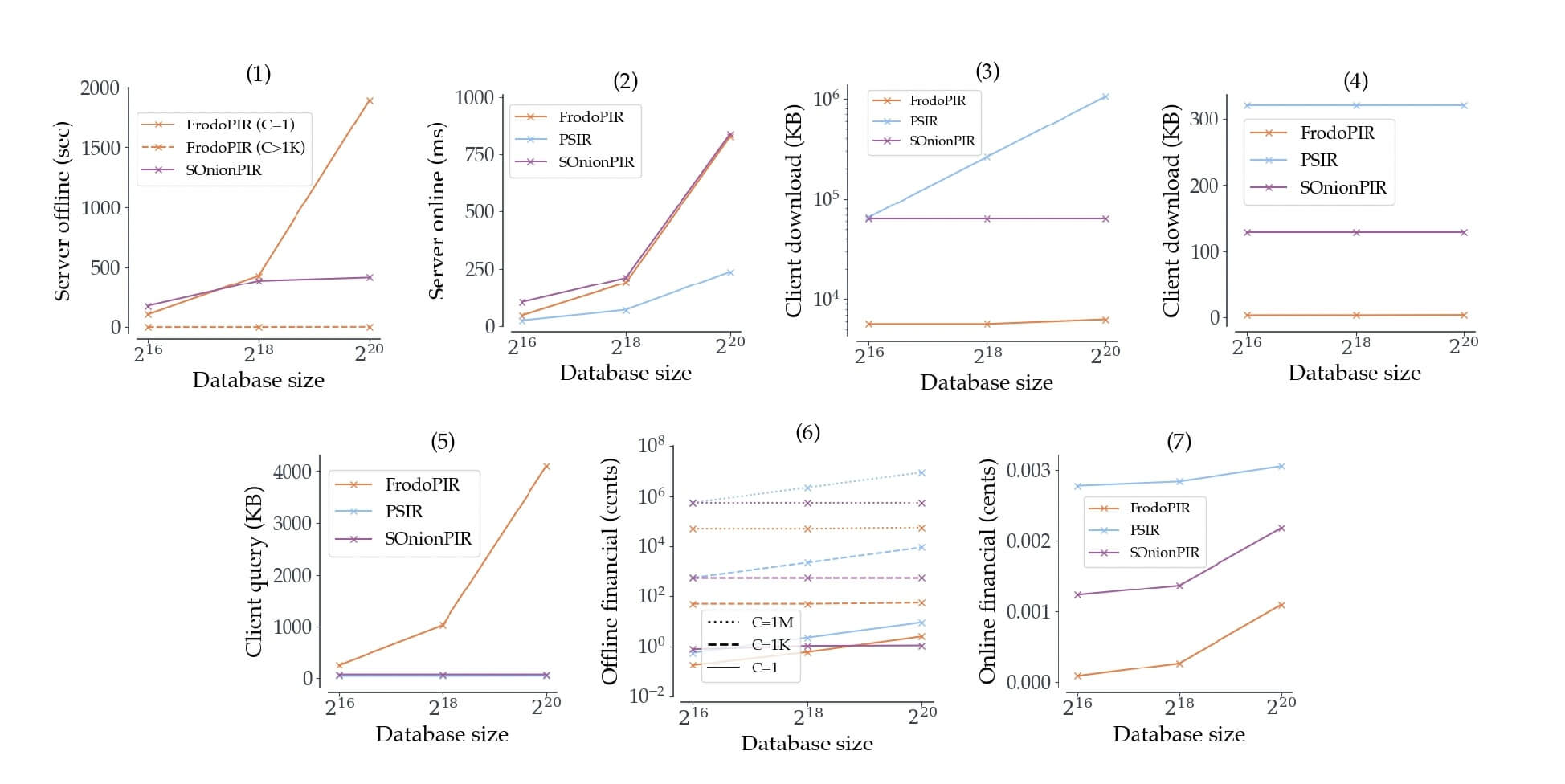
Figure 3: Comparison of FrodoPIR with other PIR schemes
So, what is next, and how can Brave users expect to see FrodoPIR implemented? At Brave, we care about deploying privacy-preserving schemes that make the Internet private and safe. One of our next efforts is to have a credential checker: any credential entered through the Brave browser (like, for example, passwords) can be checked against known breached databases. This can provide a safe mechanism to signal users to, for example, change their passwords. But such checking (the queries launched against the breached database) should be private. And, on this, FrodoPIR shines as a mechanism to provide privacy in a financially cheap and efficient fast way.
To read more about our FrodoPIR scheme, you can find details here. The paper has been accepted to the Proceedings on Privacy Enhancing Technologies (PETS), Vol. 2023, Issue 1, and will also appear here.
This content originally appeared on Brave's latest news on Brave Browser and was authored by Brave's latest news on Brave Browser
Brave's latest news on Brave Browser | Sciencx (2022-12-21T00:00:00+00:00) FrodoPIR: a new privacy-preserving approach for retrieving data. Retrieved from https://www.scien.cx/2022/12/21/frodopir-a-new-privacy-preserving-approach-for-retrieving-data/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
