This content originally appeared on Level Up Coding - Medium and was authored by Vikram Gupta
Sorting Algorithms
Know complete analysis of the Heap Sort Algorithm.
This article is about designing, visualizing, and analyzing the Heap Sort algorithm. After reading this article you will be able to answer most of the questions related to the Heap Sort algorithm.
What Is A heap?
The (binary) heap data structure is an array object that we can view as a nearly complete binary tree as shown in the below figure. Each node of the tree corresponds to an element of the array. The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point.
Let’s see two different representations of a heap:
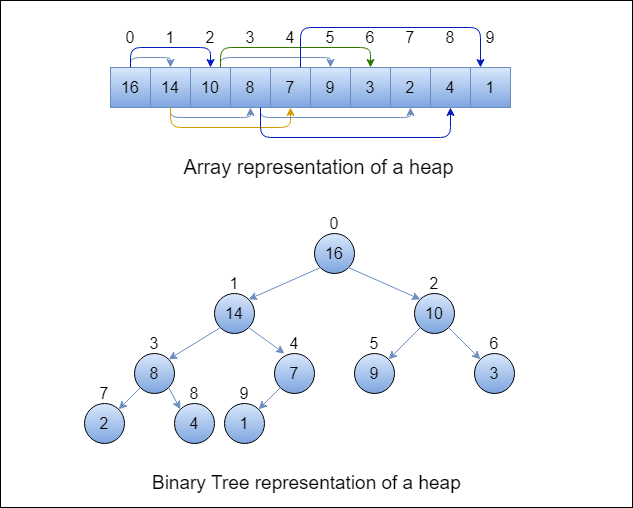
Note that I’m assuming the index starts from 0.
In the above heap(nearly complete binary tree) the Parent, LeftChild, and RightChild can be computed in constant time as these are mostly one instruction.
Following are the way to find the index for the left, right, and parent node index.
Parent(i)
return ⌊(i-1)/2⌋;
--------------------------------------------------------------------
LeftChild(i)
return 2*i+1;
--------------------------------------------------------------------
RightChild(i)
return 2*i+2;
In the above heap example if the node index is i = 3 then the left child node index will be 2*3+1 =7 and the right child node index will be 2*3+2 = 8
Also, note that the height of the above tree is 3, and the value 8 at index 3 has a height of 1. Similarly, value 1 at index 9 has a height of 0.
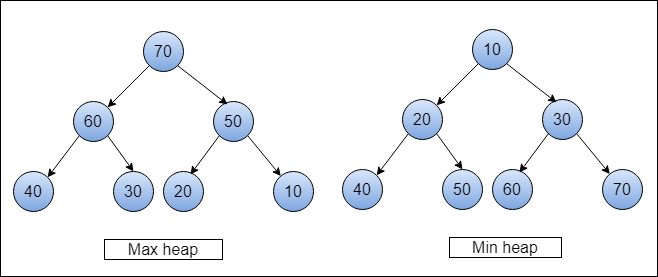
What Are Max-heap and Min-heap?
A heap(nearly complete binary tree) is called a max heap when the parent node is greater(or equal) than its left and right child nodes. In the below figure, you can see each parent node is greater than its left and right child nodes.
In max heap largets element is stored at the root of the binary tree.
A heap(nearly complete binary tree) is called a min-heap when the parent node is smaller(or equal) than its left and right child nodes.
In min heap smallest element is stored at the root of the binary tree.

We’ll use max-heap for sorting the array elements.
How Does Heapsort Algorithm Work for Sorting in Increasing Order?
- Build a max heap from the given array.
- At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of the heap by 1. Finally, heapify the root of the tree.
- Now repeat step 2 till the size of the heap is greater than 1.
1. How to Maintain the Max-heap Property?
- We can maintain the max-heap property by calling the maxHeapify method on non-leaf nodes. All the leaf nodes already satisfy the max-heap property as they do not have children.
- When the maxHeapify method is called with a node having index ‘i’ then the node is compared with its left and right child. The largest node among the parent node, left and right children nodes are found and the largest node gets swapped with the parent node. As the parent node may have shifted down, we have to recursively heapify the left or right subtrees to the heap to maintain the max-heap property.
Let’s see an example to heapify a node (consider the node at index i=1) which violates the max-heap property:
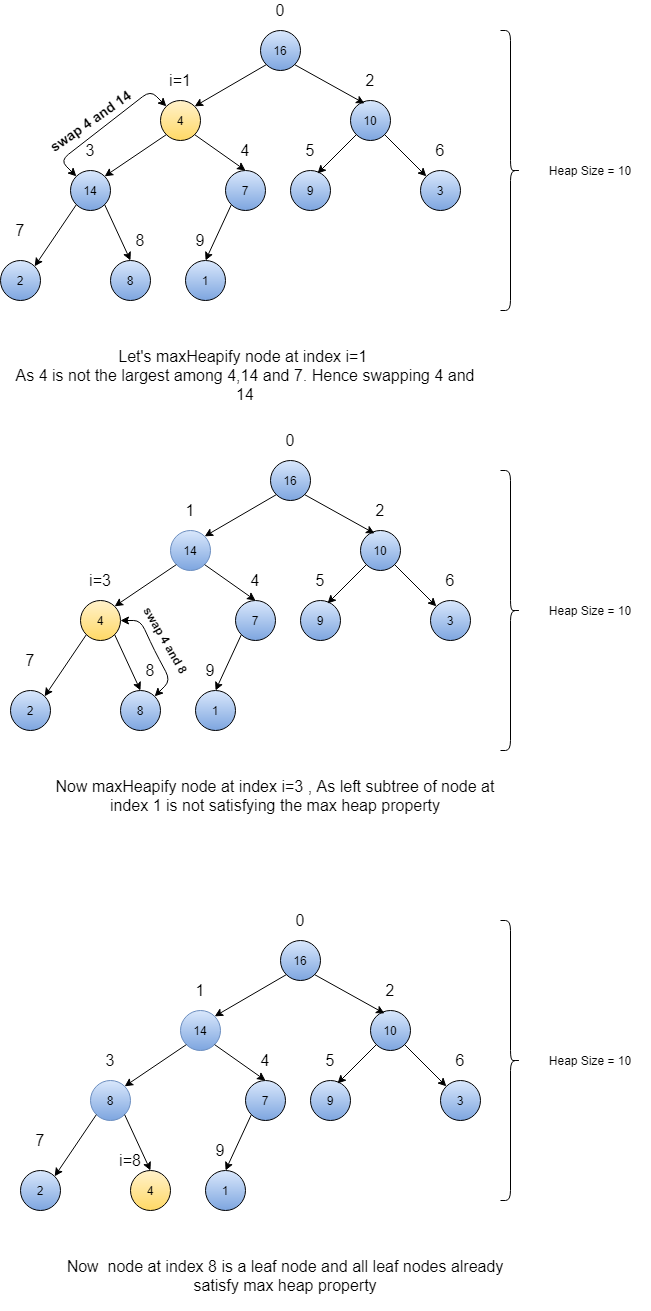
Now below is the piece of code which does the same job as what we did in the above example. While reading the code try to understand the comments also.
Let’s Analyse the Time Complexity for the maxHeapify Function:
- The maxHeapify involves the finding of the largest index which takes a constant amount of time on any machine.
- But the maxHeapify function is recursively called for maintaining the max heap property on the affected subtree. Hence one has to travel from the given node to the leaf of a particular subtree in a worst-case scenario. For example, if a node has a height ‘h’ then the maximum recursive calls to maxHeapify() will be ‘h’ only.
Now a tree with n nodes has a height of logn and hence the worst-case time complexity for maxHeapify() is O(logn).
2. How to Build the Max-heap from the Given array:
- When all the nodes of a heap satisfy the max heap property then we can say that we have built the max heap.
- As all the leaf nodes of a heap already satisfy the max heap property, we can start checking the max heap property from the node which has at least one child and calling the maxHeapify method for each such node for maintaining the max-heap property.
- Hence in the below buildMaxHeap method, the loop initialization started with ((length of array/2) — 1), and afterward for each node maxHeapify method is called to maintain the max heap property.
Let’s see an example of how to build a max heap:
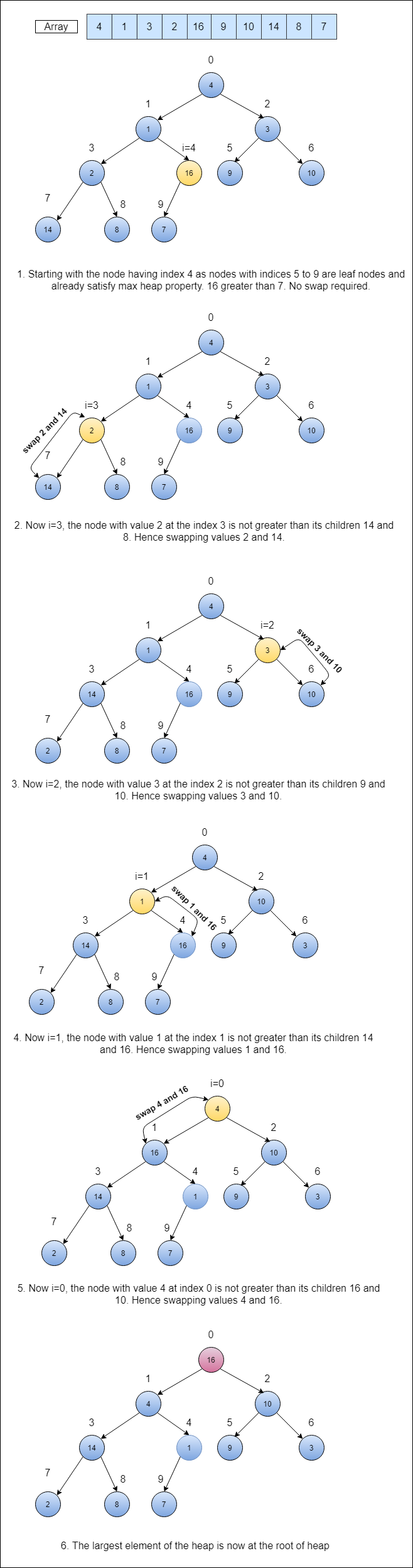
Below is the code for building the max heap from the given array:
Time Complexity Analysis of buildMaxHeap Function:
- As you can see that a loop is running for half of the array(heap) elements and for each node maxHeapify method is called which takes at most O(logn) time. Hence we can say that buildMaxHeap will take at most O(nlogn) time.
- But if you give deeper look at the above ‘for’ loop then you will realize that for each maxHeapify call the value of the variable ‘i’ is different which means the recursive calls for maxHeapify will have a different height for each node(i). This height will be equal to the height of node(i).
Now we can say that our tighter analysis relies on the properties that an n-element heap has height ⌊ logn ⌋ and at most ⌈ n/2^(h+1)⌉ nodes of any height h. For example, if the given height is 2 (h=2) in the heap and the no of elements in the heap is 10 (n=10), then the heap has at most 2 nodes with height 2 (h=2).[You can verify this in the above example we discussed].
If ‘h’ is the height of a node then there would be at max ‘h’ calls to maxHeapify(). Hence O(h) is the worst-case time complexity for the node having a height ‘h’ and there would be at most ⌈ n/(2^(h+1))⌉ nodes of height ‘h’, considering ’n’ is no of elements in the heap.
Let’s sum all the function calls to maxHeapify() from height h=0 to ⌊ logn ⌋ :
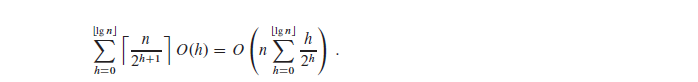
The result of the above equation is O(n). Hence we can say that the worst-case time complexity of buildMaxHeap() is O(n) and NOT O(nlogn).
3. Sorting Array Elements Using Heap-sort:
Once we are ready with the Max heap, we can iterate over heap elements one by one and each time swapping the root and last node of the heap and reducing the heap size by 1. For each swap, we must heapify our heap so that it maintains the max heap property for the next iteration.
As the root of the heap is exchanged with the last node of the heap we must pass the index of the root that is 0 for heapify and reduced heap size (that is ‘i’ in the below code).
Now Let’s Analyze the Time Complexity of Heapsort:
- Building the max heap(buildMaxHeap Method) takes O(n) time as we discussed above while building the max heap.
- The next loop iterates for each heap node and calls the maxHeapify() method which takes O(logn) time at most each time. Hence the heapSort has time complexity as O(nlogn).
Best and Worst-Case Time Complexity of Heap-Sort is O(nlogn). It is independent of distribution of array elements.
4. Driver Method to Test the Sorting :
To test the above code let’s pass an array with random numbers to sort them in ascending order using the heapSort algorithm.
Output:
Sorted Array is :
1 2 3 4 7 8 9 10 14 16
Is Heap Sort Stable?
Heapsort is not a stable algorithm.
Consider the Heap sort example below to understand this.
Consider array 20 10a 10b 9 8 7 (this array is already in max-heap format).
Here 10a = 10b just to differentiate the order, we represent them as 10a and 10b .
Now heapsort first removed 20and placed in the last index then 10ais removed and placed before 20and then 10bis removed and placed before 10a. So after heap sort, the array looks like the below:
7 8 9 10b 10a 20.
It does not preserve the order of elements (10a and 10b )and hence it isn’t stable
Is Heap Sort In-place?
It uses extra space only for storing recursive function calls but not for manipulating the input hence it is an In-place.
That’s all for this article.
Follow Vikram Gupta for similar content.
Reference: Introduction to algorithms.
Visualizing, Designing, and Analyzing the Heap Sort Algorithm. was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Vikram Gupta
Vikram Gupta | Sciencx (2023-02-17T15:50:55+00:00) Visualizing, Designing, and Analyzing the Heap Sort Algorithm.. Retrieved from https://www.scien.cx/2023/02/17/visualizing-designing-and-analyzing-the-heap-sort-algorithm/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
