Unfold Combinatorics Family Problems

This content originally appeared on Level Up Coding - Medium and was authored by Waleed Khamies

Unfold Algorithm Coding Interviews For Data Scientists

Chapter 2: A Deeper Look Into Backtracking Approach.

Table of Contents

1. The Lottery Ticket.
2. Permutations.
3. Combinations.
4. Combinations Sum.
5. Subsets.
6. Letter Combinations of a Phone Number.
7. Generate Parentheses.
8. Family Patterns.
9. Recap.
10. Next Post.

1. Introduction

A young man called Wail has received a $1 million lottery ticket and he has to decide what he wants to spend this money on. He scratched his mind and started thinking about what to do with this money. There were many things he wanted to buy and many activities he wanted to do.

At that time, the most important thing to Wail was to settle down and build a healthy relationship with his fiancée. So, he decided to secure three things: Buying a house, Buying a Car, and organizing the wedding ceremony. But, he had the following question:

in which order does he have to accomplish these things?

So, he started to draw the following scenarios:

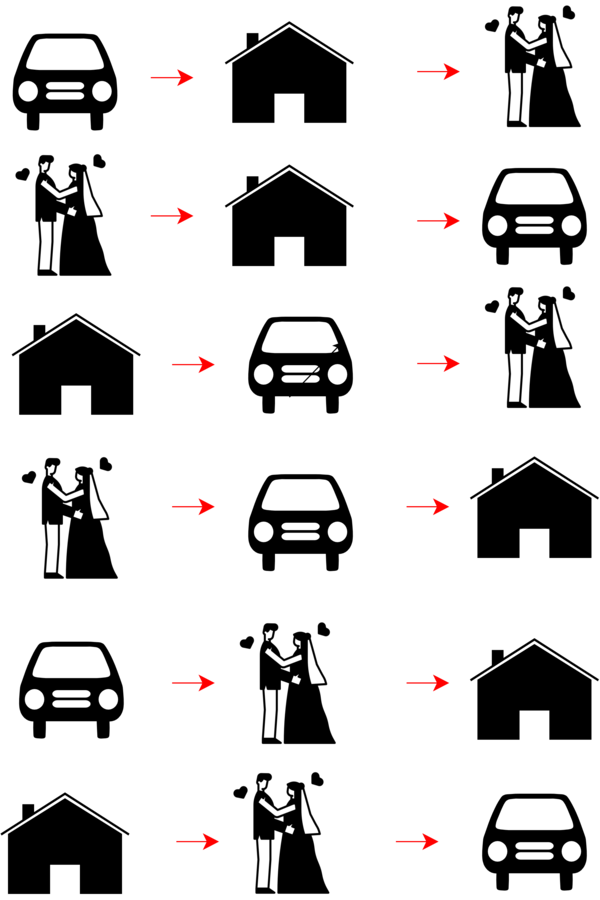
Finally, after a long discussion with his fiancée, he chose the option to get married, buy a house, and then buy a car. Wail was keen to let his future partner be part of the decision-making, what a gentleman!

This story is just an example of how decision-making is made throughout our life, in this example:

1. Wail defined a goal that he wanted to accomplish.
2. He listed all the actionable goals that he could do to help him achieve his bigger goal.
3. He listed all the sequences that he could order with them these actionable goals.
4. He chose one sequence that best served his main goal.

Interviewers adore the types of questions that include such patterns. So, in this post, we will discuss Combinatorics Family Problems. It is one of the most important families in this series because many coding interview questions come from this Family.

Also, this Family shares a solution pattern considered one of the most used techniques among problem solvers. Therefore, being able to master these types of questions is a crucial step for acing any coding interview. So without further ado, let us get started!

In this post, We will discuss the following problems:

• Permutations
• Combinations
• Combinations Sum
• Subsets
• Letter Combinations of a Phone Number
• Generate Parentheses

Let us get started!

2. Permutations

We will start this family with the “Permutations” problem. This problem is considered the main building block for other problems in this family. You will not find any problem in this family that not having a pattern from the permutations problem.

2.1 Problem Description

The problem is formalized as follows:

We are given a list of integers and want to find all the possible permutations that can be formed from this list.

Ok, let us take this example:

2.2 Example

Input: nums = [1,2,3,4]
Output: [[1, 2, 3, 4],[1, 2, 4, 3],[1, 3, 2, 4],[1, 3, 4, 2],
[1, 4, 2, 3],[1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3],
[2, 3, 1, 4],[2, 3, 4, 1],[2, 4, 1, 3],[2, 4, 3, 1],
[3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1],
[3, 4, 1, 2], [3, 4, 2, 1],[4, 1, 2, 3], [4, 1, 3, 2],
[4, 2, 1, 3],[4, 2, 3, 1],[4, 3, 1, 2],[4, 3, 2, 1]]

2.3 Brute Force Solution

In math class, we learned that the number of possible permutations of n objects is calculated with this formula:

In this problem, k = n. The easiest way to think about this problem is by visualizing those permutations as a tree; each path in the tree represents a valid permutation. To solve this problem, we must traverse this list of integers and visit all the paths in the tree. In other words, we are interested in doing a tree traverse in a list of integers to find all the valid paths that represent our pursued permutations.

Let us take the above example, suppose that we are given list nums = [1,2,3,4], and we aim to find all the possible permutations from this list. If we apply the tree analogy to this example, each subtree will represent a permutation set, and each tree path will represent a possible permutation. The figure below represents the permutation set that starts with the number “1”.

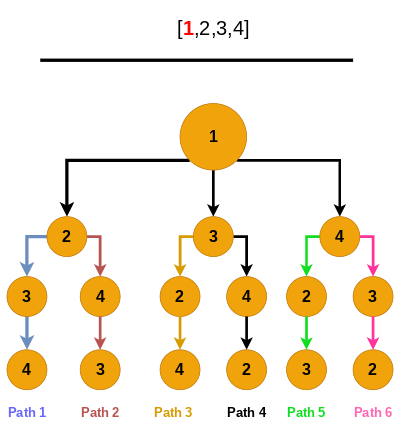
If we traverse this tree using the Depth-First Search algorithm (DFS), the paths will be as follows: [1,2,3,4], then [1,2,4,3], then [1,3,2,4], then [1,3,4,2], then [1,4,2,3], and finally [1,4,3,2] which are considered valid permutations.

The code below shows that we used a “loop” operator to traverse the list of numbers horizontally and a “recursive function call” to traverse them vertically. First, we move one step in the horizontal direction, take the next element in the list as a root to the next subtree and store it in the “path” variable. Second, we go in the vertical direction to build this next subtree.

Thus, the horizontal expansion allows us to increase the width of the tree:

for i in range(len(nums)): # Horzintoal expansion.

While the vertical expansion ensures we grow the length of the tree paths:

for i in range(len(nums)): # Horzintoal expansion.
  dfs(nums[0:i] + nums[i + 1 :], path + [nums[i]], result) # Vertical expansion.

Finally, we stop the vertical expansion when we reach a leaf node and the horizontal expansion when we visit all the numbers in the list. This is done by just those three lines:

# When the there are no more items in the list that belong to each node, 
# the recursion will stop.
if len(nums) <= 0: 
  result.append(path)
  return

These two operations happen in the “+S” order. The plus sign “+” means storing the node's value first, while the “S” letter means building all the subtrees under that node. The figure below shows all the subtrees and paths of our example:

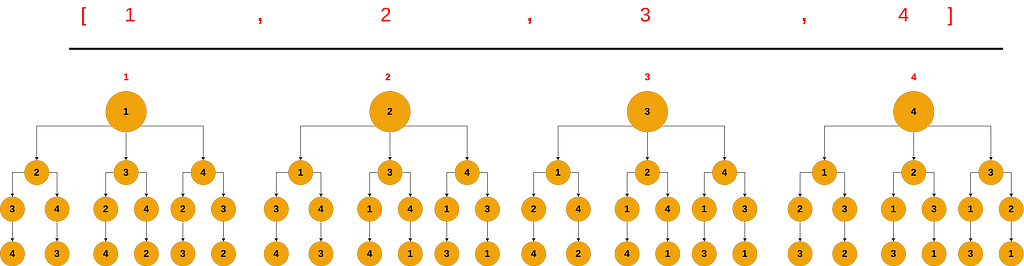
Now, let us see the full code that generates all the permutations according to the above algorithm :

Time complexity:

The time complexity for this solution will be:

The intuition of this time complexity needs a bit of explanation. Let us take the above example. We know that the permutation of a list of size = 4 and k = 4 is 4! which is equal to 4! recursive function calls. But, to get a single permutation from those 4! permutations, our “dfs” function should call itself 4 times, representing the time needed to traverse a single path in the tree. (see the figure above).

Space complexity:

which is equal to the memory space needed to store those permutations.

3. Combinations

The combination problem is similar to the permutations problem, but instead of considering all the permutations as outputs, we take subsets from them with pre-defined lengths. Here is the problem definition:

3.1 Problem Description

We are given a list of integers and we want to find all the possible combinations of k numbers, where k represents the number of chosen objects from the list.

3.2 Example

Input: nums = [1,2,3,4], k = 2

Output: [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]

3.3 Solution

The solution will be similar to the permutation solution, except that we will do backtracking whenever the length of our path equals k. Wait, wait, wait Waleed! What the heck is backtracking? Alright, let us talk about it:

Backtracking is simply to stop our recursive algorithm from execution and consider part of the problem solutions becasue of some constraints.

Backtracking often comes implicitly with recursion, however, to apply the backtracking technique, we need three things:

1. A Goal (Base Condition): We need a goal that stops our recursion.
2. Constraints: We need a set of constraints to stop us from considering some solution paths.
3. Options: We need a set of options to select from.

Now, let us get back to our above example. Our goal is to stop when we get all the possible combinations. But simultaneously, we will impose one constraint by stopping our search whenever we reach a certain path length (len(path) =k). At each time, we have one option that we select by going one step in the vertical direction taking the next sublist to build the next subtree.

for i in range(len(nums)):
# pass nums[i+1:] to the next recursive call to build the next subtree.
  dfs(nums[i+1:],  path+[nums[i],], result)

Below is a visualization of all the combinations that starts with 1 when k = 2. The figure shows that if we start traversing num = [1,2,3,4], instead of storing all the nodes along each path, we will take just the first two nodes starting from the tree's root node.

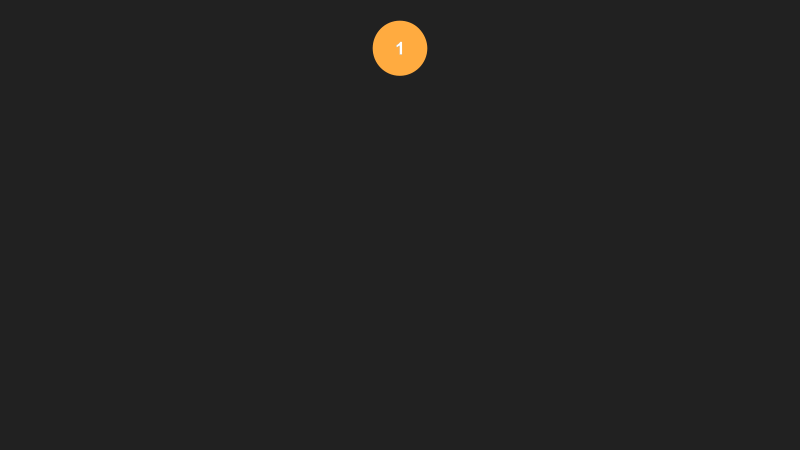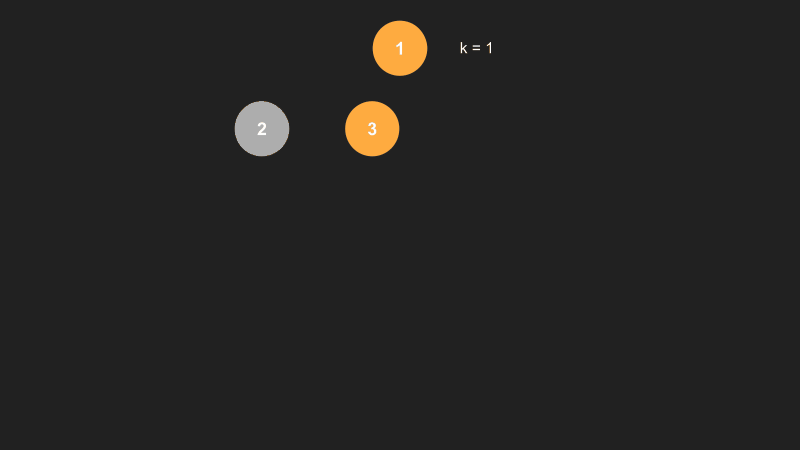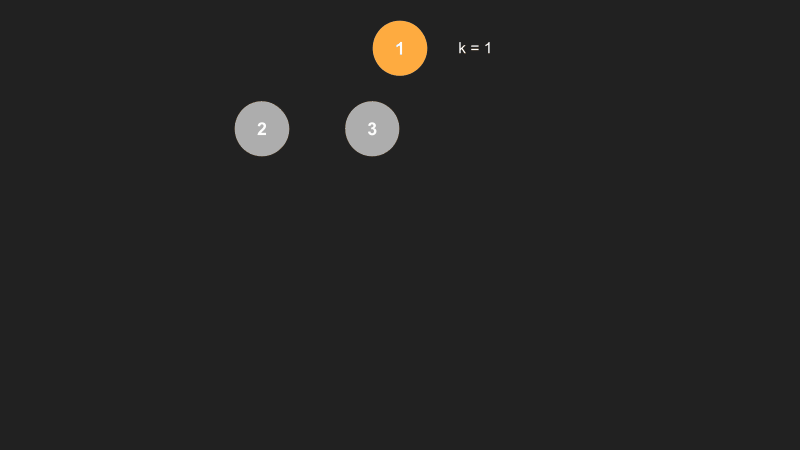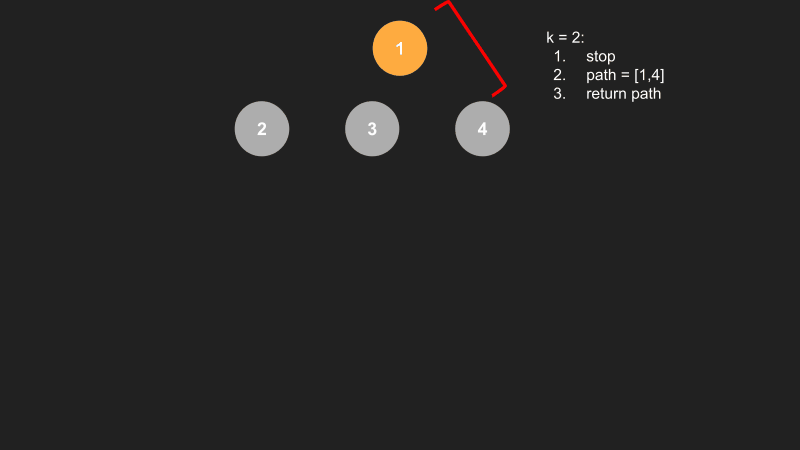
Compared with the permutations problem, we can observe that the number of paths shrank, as the combination operation cares about unique permutations and not considering the repetitive ones. ( i.e., [1,2] is the same as [2,1]). Here is a figure showing all combinations of this example:

Time complexity:

The time complexity will be equal to the time needed to traverse a path to generate a single combination multiplied by the number of all possible combinations:

where n is the total number of elements in the list, and k is the number of chosen elements from the list.

Space Complexity:

The space complexity represents the memory space needed to store all possible combinations, which equals to:

4. Combinations Sum

Let us jump to another version of the combinations problem we saw earlier. In this version, we have a target and want to find any combination whose sum equals this target. Does this remind you of a similar problem we encountered in this series? Hmmm, Yes, KSum problem!

4.1 Problem Description

This problem could be defined as follows:

We are given a list of integers and we want to find all the possible combinations of k numbers that their sum equal to a given target, where k represents the number of chosen numbers from that list.

4.2 Example

Let us take this example:

Input: nums = [1,2,3,4], target = 4

Output: [[1, 3], [4]]

Here we want to find all the combinations whose sum equals 4.

4.3 Solution

To solve this problem we will just extend the combinations problem code. We will add a variable target which will be subtracted from the nodes' values along each possible path. Then, we will return any path that gets that target value to equal zero. In other words, for each path p, we are interested in returning the path that satisfies the following condition:

Now, let us see how backtracking’s components look like here:

1. Goal: To make the target equal to zero.

if target ==0:
  return

1. Options:

• We subtract a node’s value from the target.
• Then, we go one step in the vertical direction to build the next subtree.

for i in range(len(nums)):
# 1) we execute target-nums[i].
# 2) pass nums[i+1:] to the next recursive call to build the next subtree.
  dfs(nums[i+1:],  path+[nums[i],], result, target-nums[i]) 

1. Constraints: To not return any combination whose sum is bigger than the target.

if target < 0:
  return

Below is a figure explains how the full algorithm works:

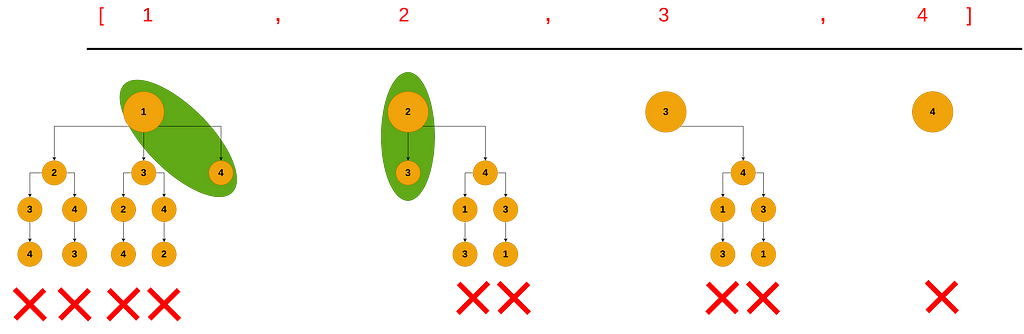
We are looking for a group of combinations whose sum equals 5. The green ellipse shows possible solutions, whereas the red crosses represent solutions or paths the algorithm explored and found invalid.

Time complexity:

Similar to the combinations problem, the time complexity will be equal to the time needed to traverse a path to generate a single combination multiplied by the number of all possible combinations:

where n is the total number of elements in the list, and k is the number of chosen elements from the list.

Space Complexity:

And the space complexity represents the memory space needed to store all possible combinations:

Break Time!

Now, I would like you to have a break before continuing the next part of this series. GO, GO, and drink some water or juice, I’ll be waiting for you!

Ok ok ok, you could not resist skipping the break, but anyway welcome back again!

5. Subsets

“Subsets” is an interesting problem in this family because it shows exactly how the solutions to these family problems are built upon each other. We will see how the solution to the subsets problem is just a concatenation of a series of combinations!

5.1 Problem Description

In math, we learned that the power set of a set S is the set that contains all the possible subsets from S, which includes the empty set { } and S itself. So, in this problem:

We are given a list of integers, and we want to find the power set of this list.

5.2 Example

A simple example:

Input: num = [1,2,3]

Output: [[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]

5.3 Solution

A simple way to solve this problem is by approaching it as a combination problem, how is that Waleed?!. Ok, we can notice that a power set of a list num with size = n is just the set of all the combinations of that list from k = n to k =0:

P(num) = ( C(num, n), C(num, n-1), C(num, n-2), …, C(num, 0) )

Using the example above where num=[1,2,3] with size = 3, the powerset of num will be:

P(num) = ( C(num, 3), C(num, 2), C(num, 1), C(num, 0) )

Where:

C(num, 3) = [1,2,3]

C(num, 2) = [[1, 2], [1, 3], [2, 3]]

C(num, 1) = [[1], [2], [3]]

C(num, 0) = [[ ]]

Now let us see how we can write this algorithm by just extending the combination problem solution as follows:

We can notice two new things in the combination code:

1. Removing subsets duplicates Section

To make sure that we do not have duplicates among the subsets, i.e. [ …,[1,2], …, [2,1], …], we will skip them by adding:

nums = sorted(nums
#            ...
#            ...
#            ...
if i > 0 and nums[i] == nums[i - 1]:
  continue
# .... ..... ..... ..... .....

2. Combinations concatenation Section

Here where we concatenate all the combinations

for k in range(0, n + 1):
  result = []
  path = []
  dfs(nums, k, path, result)
  final_result = final_result + result # concatenation

Time complexity:

The time complexity of this problem will be a combination of the number of combinations needed multiplied by the time that is needed for every single combination.

Space Complexity:

The memory space that is needed for this solution is equal to the number of all combinations in combination sets. ( Cₙ,…C₀)

6. Letter Combinations of a Phone Number

6.1 Problem Description

Another interesting problem in this series is the letter combinations of a Phone number. In this problem:

Given that we can access a hashmap that maps each number to a string. Find all the letter combinations we can make if we are provided with a phone number.

6.2 Example

Input: digits = “23”
Output: [“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]

6.3 Brute Force Solution

The naive way to solve this problem is by using three loops. First, we will loop over the digits, and for each digit, we will map it to its corresponding string using the given hashmap. Second, while we are inside the first loop, we will create another loop over the characters that are related to each string. Finally, we will create a loop over the previous results produced by the last step of the concatenation, i.e result = [ “ad”, “ae”], and add each character to the strings inside the result list. Let us see the code below:

Time Complexity:

The time complexity of this solution will be;

Where n = number of digits. We can see this time complexity has two components, linear component O(n) and exponential component O(4ⁿ). The linear time is a by-product of looping over the digits list ( the first loop). The exponential time complexity results from looping over the “result” list, but why? Let us take our previously mentioned example where digits = “23”.

At the beginning result = [ ], the first digit 2 will be mapped to “abc”. Then we will loop over the empty result list and concatenate each character in “abc” to the empty string “ ” in the result list to get result=[a, b, c].

In the second iteration, the second digit 3 will be mapped to “def”, then we will loop over the result = [a, b, c] and concatenate each character in “def” to each character in the result, which will update the result list to be: result = [ad, ae, af, bd, be, bf, cd, ce, cf].

Ok, Waleed, 2x4² = 2x16 = 32, and here we got 2x3² = 2x9=18, how is that possible?! You are right my friend!! But 4ⁿ is for the worst-case scenario when we have a number with 4 letters like 7 or 9.

Space Complexity:

The algorithm will use memory that:

It is exponential in space because we store these combinations inside the result list.

6.4 DFS Solution

Did we hear the word combination again?! Oh yeah, another way to solve this problem is by using the depth-first search (DFS) algorithm to find those combinations. Yes, in the same way, we solved other problems in this family:

1. We will create an “index” integer variable to keep track of the number inside the digits list.
2. We will create a “path” string variable to keep track of each valid path that the algorithm approaches it.
3. We will create a “result” list to collect the combinations.
4. Then we will call “dfs” function which builds a tree and store each path to the result list.

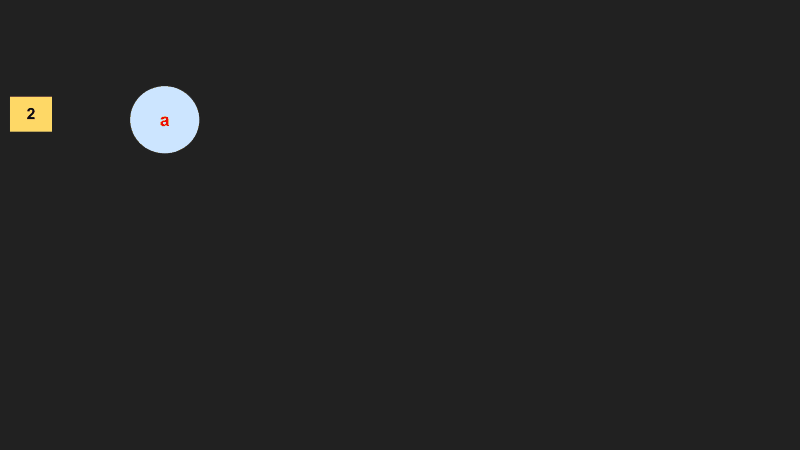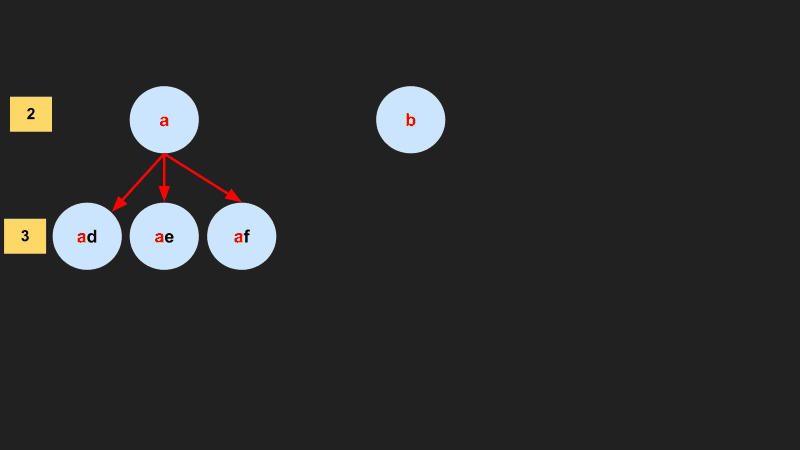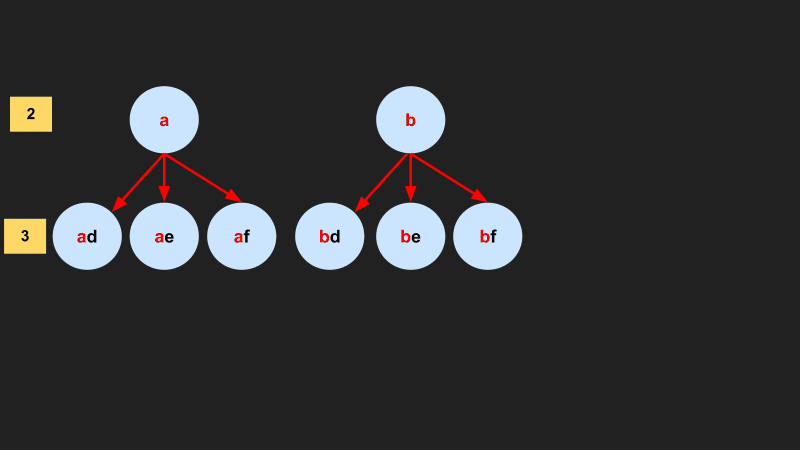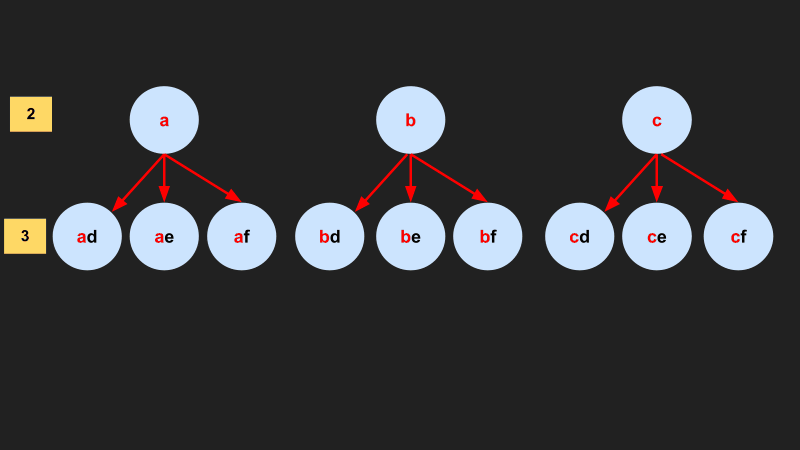
The “dfs” function below is executed as the previous diagram shows. Each leaf node in the diagram represents a call to the “dfs” function.

Time Complexity:

The time complexity will also be:

Because each phone digit will have at most 4 characters, then if we have n digits, the “dfs” function will be called for each character corresponding to the n digits. This is an exponential behavior with base 4 or O (4ⁿ).

Space Complexity:

The space complexity is the same as the brute-force solution, as we still need space to collect those combinations.

7. Generate Parentheses

7.1 Problem Description

Generate Parentheses is one of the best examples if you want to study the “Backtracking” technique and DFS algorithm.

Given an integer n, represents the number of generated parentheses, we are asked to generate all valid parentheses.

7.2 Example

Input: n = 3
Output: [“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]

7.3 Brute Force Solution

Coming up with a brute-force solution is challenging compared to the previous solutions we saw in this series. However, the main idea is to generate all possible parentheses (finding all possible solutions in the solution space), then filter them to get the valid ones.

Our brute-force solution to this problem could be as follows:

1. Generate a string having all the parenthesis pairs. For example, if n = 2, our pairs-string will be : pairs-string = “()()”
2. Traverse the pairs-string recursively using the DFS algorithm to find any possible combination.
3. Filter the combinations list to find all the valid parentheses and return the result.

Our following code explains these three steps as follows:

1. To create pairs-string, we defined:

sequence = "()" * n

2. To find any possible combination, we defined the following:

dfs_generate(sequence, path, result)

3. To filter the combinations, we defined the following:

is_valid_parenthesis(string)

Here is the full algorithm:

Time Complexity:

The time complexity of this solution will be:

This is equal to the time the “dfs_generate” function takes to generate all possible solutions. For example, if n = 2, then sequence= “()()”, which will result in having 4! combinations!

Space Complexity:

For the space complexity, we have:

Because we save every possible combination in the result list, the worst size of this list will be when all these possible combinations become valid.

7.4 Optimized Solution

Can we reduce this time complexity? Yes, we can slightly optimize the time complexity for the brute-force solution with our lovely technique, “Backtracking”!

The main idea is that we will backtrack whenever we see a combination of parenthesis that does not follow our constraints.

In this problem, we define opening_count and closing_count variables to represent the number of opening parentheses and closing parentheses, respectively. Then, the backtracking requirements are met as follows:

• Goal: Every opening parenthesis should have a close parenthesis. This is done with this:

if opening_count == 0 and closing_count ==0:
  return 

Constraints:

_ Closing parentheses Finish First: We are not interested in combinations where the number of closing parentheses finishes while there are opening parentheses. This is done with the following:

if closing_count < 0:
  return

_ Opening parentheses Finish First: We are not interested in combinations where the number of opening parentheses finishes while there are closing parentheses. This is done with the following:

if opening_count < 0:
  return

_ We are not interested in combinations where the number of opening parenthesis is more than the closing ones

if opening_count > closing_count:
  return

Options:

1. Select an opening parenthesis “(” and pass it to the recursive function (generate).
2. Select a closing parenthesis “)” and pass it to the recursive function (generate).

In the code below, we can see that we have called the recursive functions twice, but during execution, just one function call will be executed at a time, and that is because of our constraints :).

Time Complexity:

The time complexity will be:

This is the upper bound of the nth Catalan number. To better understand this time complexity, I suggest this discussion and this too.

Space Complexity:

The space complexity will be:

Because we will use the “result” list to store the combinations.

8. Family Patterns

This Family introduced us to two of the most important patterns in the algorithm world: Depth First Search (DFS) and Backtracking.

• Depth First Search (DFS): We use the Depth-First Search algorithm to traverse the list of integers or digits. If problems require finding all possible combinations or solutions, “dfs” can be your secret weapon.
• Backtracking: Sometimes, we care about part of the solution space, and we do not want to explore and generate all possible solutions (i.e., permutations) or consider all the nodes in a tree path (i.e., combinations). In this case, using backtracking to optimize the search space is better.

9. Recap

Here is a summary of this post:

• Problems that require you to find all possible solutions → Try to use the DFS algorithm. [3][4]
• Problems that require you to find parts or subsets of solutions → Try to optimize with the Backtracking technique. [1]

10. Next Post

After a long day at your office, you got back home, and you decided to walk to have a breath of fresh air. Suddenly, the air turned black all around you… A man wearing all black loomed out of this darkness, then you were knocked out for 1 hour. After waking up …

You discovered you have been cursed with a black algorithmic magic!

Let us see what this black magic is, and who is that mysterious man!

New to this series?

New to the “Unfold Algorithm Coding Interviews For Data Scientists” series? Start from the beginning, here [link to the series list]

Any oversights in this post?

Please report them through this Feedback Form, I really appreciate that!

Thank you for your reading!

You can learn more about the date of future posts for this series through my newsletter, where I talk about Algorithms, Machine Learning, and Data Science.

If you have any other questions or comments, please do not hesitate to share them with me through Newsletter | Medium | LinkedIn | Twitter. See you soon!Resources

[1] Andrea Iacono, Backtracking explained, (2017), Medium.

[2] Karleigh Moore, Ken Jennison, and Jimin Khim, Depth-First Search (DFS), Brilliant.

[3] Computer Science, UofT, Heap, D. Depth-first search (DFS), 2002, UofT.

Level Up Coding

Thanks for being a part of our community! Before you go:

• 👏 Clap for the story and follow the author 👉
• 📰 View more content in the Level Up Coding publication
• 💰 Free coding interview course ⇒ View Course
• 🔔 Follow us: Twitter | LinkedIn | Newsletter

🚀👉 Join the Level Up talent collective and find an amazing job

Unfold Combinatorics Family Problems was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.

This content originally appeared on Level Up Coding - Medium and was authored by Waleed Khamies

Print Share Comment Cite Upload Translate Updates

APA

Waleed Khamies | Sciencx (2023-03-14T15:22:12+00:00) Unfold Combinatorics Family Problems. Retrieved from https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/

MLA

" » Unfold Combinatorics Family Problems." Waleed Khamies | Sciencx - Tuesday March 14, 2023, https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/

HARVARD

Waleed Khamies | Sciencx Tuesday March 14, 2023 » Unfold Combinatorics Family Problems., viewed ,<https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/>

VANCOUVER

Waleed Khamies | Sciencx - » Unfold Combinatorics Family Problems. [Internet]. [Accessed ]. Available from: https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/

CHICAGO

" » Unfold Combinatorics Family Problems." Waleed Khamies | Sciencx - Accessed . https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/

IEEE

" » Unfold Combinatorics Family Problems." Waleed Khamies | Sciencx [Online]. Available: https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/. [Accessed: ]

rf:citation

» Unfold Combinatorics Family Problems | Waleed Khamies | Sciencx | https://www.scien.cx/2023/03/14/unfold-combinatorics-family-problems/ |

Please log in to upload a file.

There are no updates yet.
Click the Upload button above to add an update.

You must be logged in to translate posts. Please log in or register.