This content originally appeared on Level Up Coding - Medium and was authored by Vishal Sharma
This article explores implementing and visualizing binary trees in Python, using classes and objects to represent nodes and their relationships. Binary trees are powerful data structures that provide hierarchical organization for data and have various applications, such as searching, sorting, and storing hierarchical data.

Binary trees are fundamental data structures in computer science that are used to represent hierarchical relationships between objects. In Python, binary trees can be implemented using classes and objects, providing a flexible and efficient way to store, manipulate, and search for data in a tree-like structure. This article will explore how binary trees are implemented in Python and discuss common operations such as insertion, deletion, and traversal.
Class Definition for Binary Tree Node:
In Python, binary trees can be implemented using classes, with each node in the tree represented as an object of the class. Here is an example implementation of a binary tree node:
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
In the above implementation, the TreeNode class has three attributes:
- key: Represents the value or key stored in the node.
- left: Represents the left child node of the current node.
- right: Represents the right child node of the current node.
Insertion Operation:
Insertion is the process of adding a new node to the binary tree. The insertion operation typically involves finding the correct position in the tree to place the new node based on its value. An example implementation of an insertion operation for a binary tree:
def insert(root, key):
if root is None:
return TreeNode(key)
else:
if key < root.key:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
In the above implementation, root represents the root of the binary tree, and key represents the value of the new node to be inserted. The insertion operation is recursive, and it starts from the root and proceeds down the tree based on comparing the key with the current node's key. If the key is less than the current node's key, it goes to the left subtree; otherwise, it goes to the right subtree.
Deletion Operation:
Deletion is the process of removing a node from the binary tree. The deletion operation can be more complex than insertion, as it requires handling different cases, such as deleting a leaf node, deleting a node with one child, or deleting a node with two children. An example implementation of a deletion operation for a binary tree:
def delete(root, key):
if root is None:
return root
if key < root.key:
root.left = delete(root.left, key)
elif key > root.key:
root.right = delete(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = get_min_value(root.right)
root.key = temp.key
root.right = delete(root.right, temp.key)
return root
def get_min_value(root):
while root.left is not None:
root = root.left
return root
Hereroot represents the root of the binary tree, and key represents the value of the node to be deleted. The deletion operation is also recursive. It handles different cases, such as deleting a node with no children (leaf node), deleting a node with one child (either left or right), or deleting a node with two children. The get_min_value function is used to find the minimum value node in the right subtree of a node with two children, which is used during deletion.
Traversal Operations:
Traversal is the process of visiting each node in the binary tree in a specific order. Three common methods for traversing a binary tree are in-order, pre-order, and post-order. An example implementation of these traversal operations for a binary tree:
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def in_order_traversal(root):
if root is not None:
in_order_traversal(root.left)
print(root.key, end=' ')
in_order_traversal(root.right)
def pre_order_traversal(root):
if root is not None:
print(root.key, end=' ')
pre_order_traversal(root.left)
pre_order_traversal(root.right)
def post_order_traversal(root):
if root is not None:
post_order_traversal(root.left)
post_order_traversal(root.right)
print(root.key, end=' ')
Here root represents the root of the binary tree. The in_order_traversal function performs an in-order traversal, which visits the left subtree, then the root, and finally the right subtree. The pre_order_traversal function performs a pre-order traversal, which visits the root, then the left subtree, and finally the right subtree. The post_order_traversal function performs a post-order traversal, which visits the left, right, and root subtree.
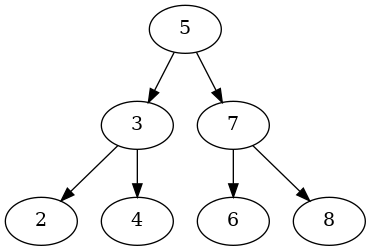
A Binary Tree:
import graphviz
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def insert(root, key):
if root is None:
return TreeNode(key)
else:
if key < root.key:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
def visualize_binary_tree(root):
dot = graphviz.Digraph()
dot.node(str(root.key))
def add_nodes_edges(node):
if node.left:
dot.node(str(node.left.key))
dot.edge(str(node.key), str(node.left.key))
add_nodes_edges(node.left)
if node.right:
dot.node(str(node.right.key))
dot.edge(str(node.key), str(node.right.key))
add_nodes_edges(node.right)
add_nodes_edges(root)
dot.render('binary_tree', view=True, format='png')
# Example usage:
root = None
keys = [5, 3, 7, 2, 4, 6, 8]
for key in keys:
root = insert(root, key)
visualize_binary_tree(root)
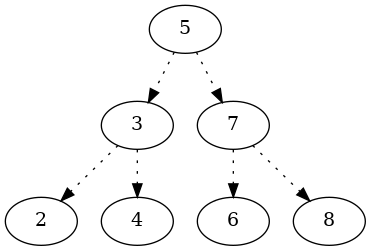
Traversals Overview:
import graphviz
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def insert(root, key):
if root is None:
return TreeNode(key)
else:
if key < root.key:
root.left = insert(root.left, key)
else:
root.right = insert(root.right, key)
return root
def inorder_traversal(root, dot):
if root:
inorder_traversal(root.left, dot)
dot.node(str(root.key), label=str(root.key))
if root.left:
dot.edge(str(root.left.key), str(root.key), style='dotted')
if root.right:
dot.edge(str(root.key), str(root.right.key), style='dotted')
inorder_traversal(root.right, dot)
def preorder_traversal(root, dot):
if root:
dot.node(str(root.key), label=str(root.key))
if root.left:
dot.edge(str(root.key), str(root.left.key), style='dotted')
if root.right:
dot.edge(str(root.key), str(root.right.key), style='dotted')
preorder_traversal(root.left, dot)
preorder_traversal(root.right, dot)
def postorder_traversal(root, dot):
if root:
postorder_traversal(root.left, dot)
postorder_traversal(root.right, dot)
dot.node(str(root.key), label=str(root.key))
if root.left:
dot.edge(str(root.left.key), str(root.key), style='dotted')
if root.right:
dot.edge(str(root.right.key), str(root.key), style='dotted')
def visualize_binary_tree(root):
dot_inorder = graphviz.Digraph(comment='Inorder Traversal')
inorder_traversal(root, dot_inorder)
dot_inorder.render('inorder_traversal', view=True, format='png')
dot_preorder = graphviz.Digraph(comment='Preorder Traversal')
preorder_traversal(root, dot_preorder)
dot_preorder.render('preorder_traversal', view=True, format='png')
dot_postorder = graphviz.Digraph(comment='Postorder Traversal')
postorder_traversal(root, dot_postorder)
dot_postorder.render('postorder_traversal', view=True, format='png')
# Example usage:
root = None
keys = [5, 3, 7, 2, 4, 6, 8]
for key in keys:
root = insert(root, key)
visualize_binary_tree(root)
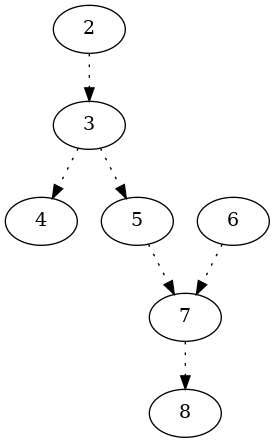
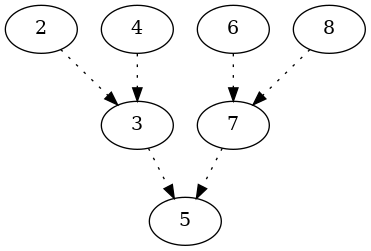
Conclusion:
The implementation of binary trees in Python can be achieved using classes and objects to represent nodes and their relationships. Binary trees are powerful data structures for organizing data hierarchically and can be used for various applications, including searching, sorting, and storing hierarchical data. Visualization of binary trees can be done using libraries like Graphviz in Python, which allows for creating graphical representations of trees in different formats, such as PNG. Understanding how to implement and visualize binary trees in Python can be valuable in solving problems that involve tree-based data structures and algorithms.
Level Up Coding
Thanks for being a part of our community! Before you go:
- 👏 Clap for the story and follow the author 👉
- 📰 View more content in the Level Up Coding publication
- 💰 Free coding interview course ⇒ View Course
- 🔔 Follow us: Twitter | LinkedIn | Newsletter
🚀👉 Join the Level Up talent collective and find an amazing job
Binary Tree Implementation and Visualization in Python was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Vishal Sharma
Vishal Sharma | Sciencx (2023-04-16T13:44:14+00:00) Binary Tree Implementation and Visualization in Python. Retrieved from https://www.scien.cx/2023/04/16/binary-tree-implementation-and-visualization-in-python/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
