This content originally appeared on Level Up Coding - Medium and was authored by Sam Armentrout
Blum Blum Shub — Golang Fun

I recently came across the Blum Blum Shub. And no, it’s not a kid’s television show like “Yo Gabba Gabba”
It’s a fascinating algorithm that can applied to many areas of mathematics.
The Blum Blum Shub is an algorithm that can be used as a bitwise pseudo-random password generator. I’ve attempted to make it usable in a modern programming langue. That is to say, I’ve created a Golang implementation of the algorithm that will actually work as a generator and will spit out a binary number at the end.
To be clear, this is not a super efficient or cryptographically secure PNRG (only as secure as the computational difficulty of factoring), but it didn’t matter to me because for the first time in my life, I, a math amateur, was able to truly understand a complex mathematical concept and apply it in a fun way with Golang.
The following screenshot is a summation of the rules outlined in the 1986 whitepaper written by… you guessed it Blum, and Blum… and Shub:

Before learning this algorithm, I would’ve said only Alan Turing can process this information.
I discovered that it’s not so bad.
We’ll do a simple example below
Step 1) Choose Two Large Prime Numbers
In the first step, we simply require two primes(preferably large) that are represented by P and Q, that, when divided by 4, have a remainder of 3.
Why the 4 Mod 3 Rule?
There is a proof reducing its security to the computational difficulty of factoring.[1] When the primes are chosen appropriately, and O(log log M) lower-order bits of each xn are output, then in the limit as M grows large, distinguishing the output bits from random should be at least as difficult as solving the quadratic residuosity problem modulo M.
Basically this implies that the quadratic residuosity problem is difficult but with a name like that it’s no wonder. But the beauty here is that you don’t have to understand it. You only have to understand that it’s difficult.
All we need to understand is that breaking the BBS algorithm in any way is difficult, because to determine the seed that generates the remaining bits in sequence requires a lot of factoring to get all the way back to the original
Anyways Continuing Step 1
[From Itechnica]
For our example, Let’s just use 11 and 23
So when 11 is divided by 4, we have 2, with remainder 3
For 23, we have 5 remainder 3
So, both of these values are valid to use as P and Q
Step 2) Calculate M
[From Itechnica]
It’s equal to P * Q
So in our case we have 253. Not so difficult hopefully
Step 3) Relative Prime Calculation ( S)
[From Itechnica]
Calculate S: We simply have to find a value where neither P nor Q is a factor
If we choose S as 84, then we’re good. It’s pretty simple
You can literally choose almost any value, as long as they
Step 4) Calculate X0
[From Itechnica]
X0 = (S)² mod 253
So 84² = 7056
And If we do Mod 253 , we get 225

Step 5) Calculate X1
[From Itechnica]
X1 = (X0)² mod m
We simply take 225² mod 253
Result of X1 = 25
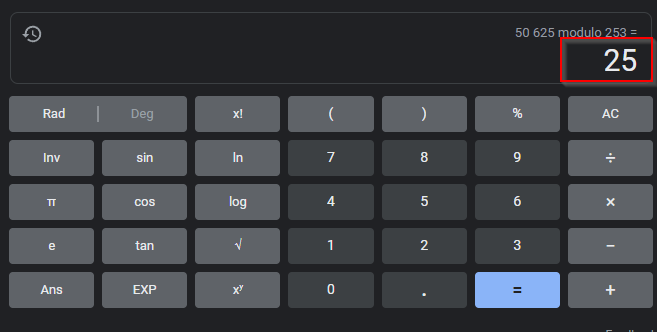
Step 6) First Psuedo-Random Value
[From Itechnica]
= B1 which is equal to X1 Mod 2
So result is
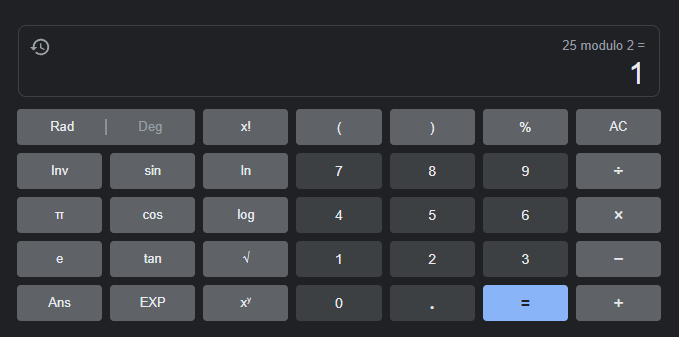
Step 7) Calculate Next Value
[From Itechnica]
Obviously here as a programming construct, we’d want to do a for loop, to loop for a certain amount of iterations, literally constructing the binary sequence bit-by-bit
All we have to do to calculate the next bit is simple
We take the previous X value. So that’d be X1 in our case
(X1)² mod m
That for us is (25)² mod 253
Which comes out to 129
When we take 129 mod 2, we get a result of 1
That means thus far we have a binary value of 11
So what does this Mean?
Well it means we created a password of : 11 (Binary)
Or 3 in decimal
Not very exciting. Or even secure.
But that’s not the point. I wanted to learn something about Pseudo-Random Number Generators. And the beauty of the BBS algorithm : It is easily provable
Let’s Use it in a Golang App!
Two Options : Run and Install Yourself, or Test Easily with My Replit Link!
Option 1) Install and Run Yourself
If you haven’t installed Golang, you can install it on windows below
I recommend Goland as an IDE or VS Code . Both autodetect the SDK you’re using
Goland can automagically creates you a nice go.mod file
VS Code is nice, but make sure your path is set properly for Go Pls and other tools — there’s an easy setup guide
https://learn.microsoft.com/en-us/azure/developer/go/configure-visual-studio-code
All I do once I’ve created a directory is create a go file that contains the main package

I called it testbbs.go and in it I included the code below (same code linked in replit)
In the terminal, really only two commands are required (assuming a main function with the name “testbbs.go”
Go build testbbs.go
Go run testbbs.go
Option 2) Replit Link
Actual Code :)
package main
import (
"fmt"
"strings" // Add this line to import strings package
)
func main() {
//x := int64(3e10)
//y := int64(4e10)
seed := 84
var x int
p := 11
q := 23
M := 253
fmt.Printf("\np:\t%d\n", p)
fmt.Printf("q:\t%d\n", q)
fmt.Printf("M:\t%d\n", M)
fmt.Printf("Seed:\t%d\n", seed)
bitOutput := ""
for i := int64(0); i < 2; i++ {
x = (seed * seed) % M
b := x % 2
bitOutput += fmt.Sprint(b)
}
fmt.Printf(bitOutput)
numZeros := strings.Count(bitOutput, "0")
numOnes := strings.Count(bitOutput, "1")
fmt.Printf("\nNumber of zeros:\t%d\n", numZeros)
fmt.Printf("Number of ones:\t%d\n", numOnes)
}
Explanation
So above, obviously hardcoded everything. It’s easier to explain that way
It’s truly simple. We have variables defined as described in our example,
P, Q , M, and Seed
A for loop makes up all the logic
for i := int64(0); i < 2; i++ {
x = (seed * seed) % M
b := x % 2A few print statements that give us a nice printed format
fmt.Printf(bitOutput)
numZeros := strings.Count(bitOutput, "0")
numOnes := strings.Count(bitOutput, "1")
fmt.Printf("\nNumber of zeros:\t%d\n", numZeros)
fmt.Printf("Number of ones:\t%d\n", numOnes)
And Boom We’re Done.
Sources
Foundation, W. (Ed.). (2022, December 22). Blum Blum Shub. Wikipedia. https://en.wikipedia.org/wiki/Blum_Blum_Shub#CITEREFBlumBlumShub1986
Itechnica. (2020). Pseudo Random Number Generator| BBS | Blum Blum Shub. YouTube. YouTube. Retrieved November 13, 2023, from https://www.youtube.com/watch?v=ScAcS2oBUXQ.
Blum, L., Blum, M., & Shub, M. (1986). A Simple Unpredictable Psuedo-Random Number Generator. Society for Industrial and Applied Mathematics, 15(2), 364–383.
Blum Blum Shub — Golang Fun was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Sam Armentrout
Sam Armentrout | Sciencx (2024-07-28T16:38:55+00:00) Blum Blum Shub — Golang Fun. Retrieved from https://www.scien.cx/2024/07/28/blum-blum-shub-golang-fun/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
