This content originally appeared on Level Up Coding - Medium and was authored by Saarthak Gupta
A Gaussian Mixture Model (GMM) is a clustering technique that assumes data is generated from a mixture of several Gaussian distributions, each with its own mean and covariance. GMMs are widely used in machine learning for clustering, density estimation, and pattern recognition.
This article will begin by explaining Gaussian mixture models and their underlying principles. Then, it will cover the algorithm used by GMM and provide a step-by-step guide to implementing it in Python.
How are Gaussian Mixture Models different from other clustering methods?
- Unlike K-means and DBSCAN, Gaussian Mixture models are capable of soft clustering, assigning probabilities of membership to each cluster. This is particularly useful when data points share properties with multiple clusters.
- GMMs can model clusters with different shapes, sizes, and orientations. This makes GMMs more flexible in capturing the true structure of the data.
- GMMs can handle complex datasets where features are correlated.
- GMMs can also be used for anomaly detection.
Key Concepts
What is a Gaussian Mixture Model?
A Gaussian Mixture model is a model where probability density is given by a mixture of Gaussian distribution.
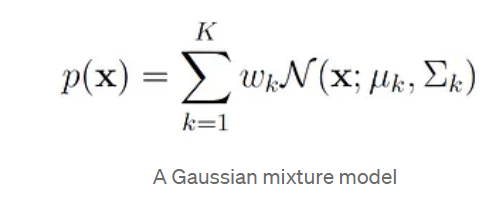
where:
- x is a d-dimensional vector.
- μₖ is the mean vector of the k-th Gaussian component.
- Σₖ is the covariance matrix of the k-th Gaussian component.
- wₖ represents the mixing weight of the k-th component, where 0 ≤ wₖ ≤ 1 and the sum of the weights is 1. wₖ is also referred to as the prior probability of component k.
- N(x; μₖ, Σₖ) is the normal density function for the k-th component.
The normal density function differs for univariate(1-dimension) and multi-variate (multi-dimensional) data.
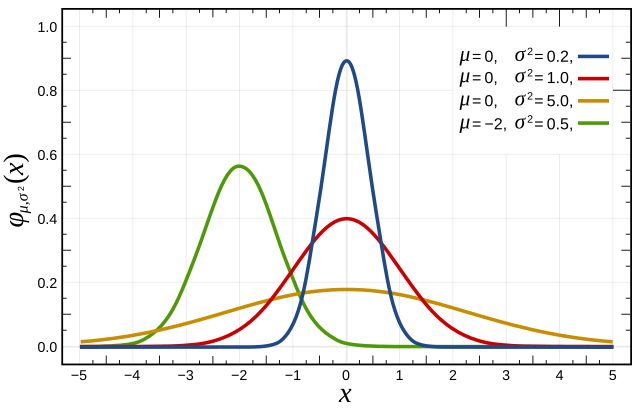
1. Univariate Normal Distribution
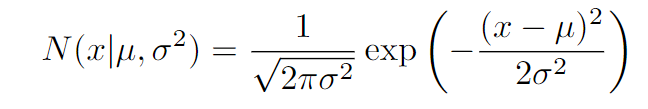
2. Multivariate Normal Distribution
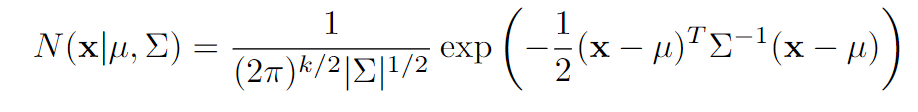
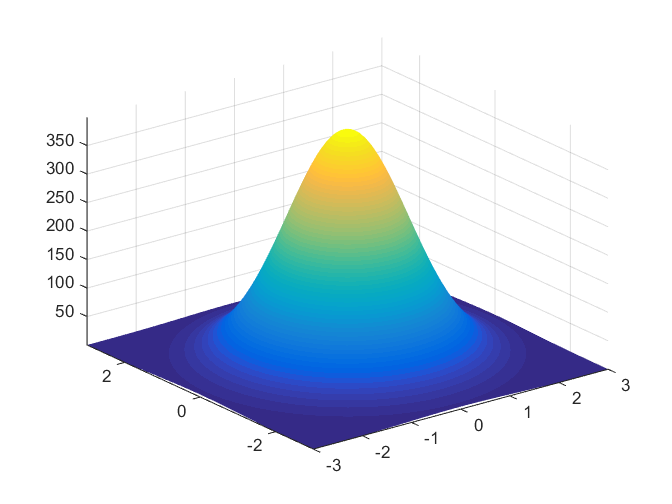
Covariance Matrix:
It generalizes the notion of variance to multiple dimensions and provides a measure of how much two random variables change together.
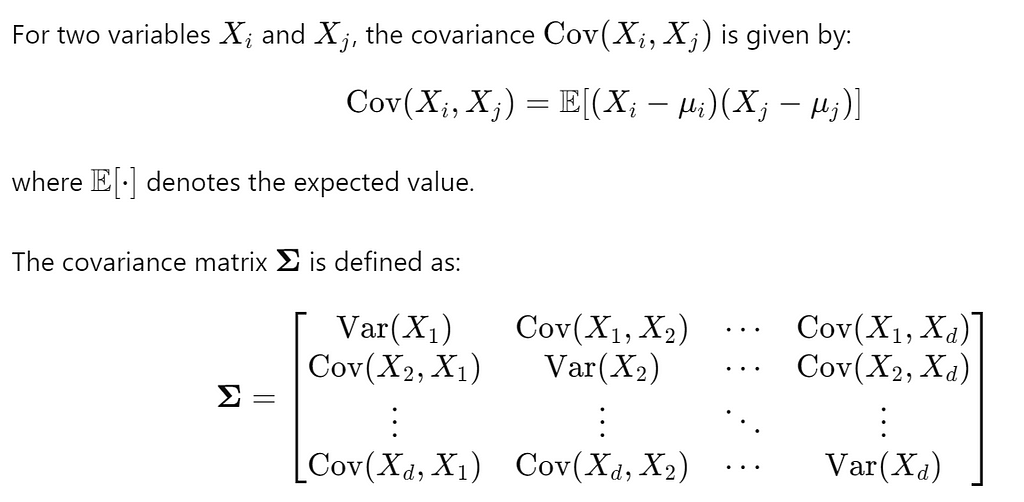
covariance measures the extent to which two variables change together. A positive covariance indicates that the variables tend to increase or decrease together, while a negative covariance indicates that when one variable increases, the other tends to decrease.
How Does GMM Work?
GMMs tell us how likely it is for a data point to belong to a particular distribution. for each point, we calculate the likelihood(responsibility) for it to belong to a particular distribution then we update the parameters of all the distributions based on the observations.
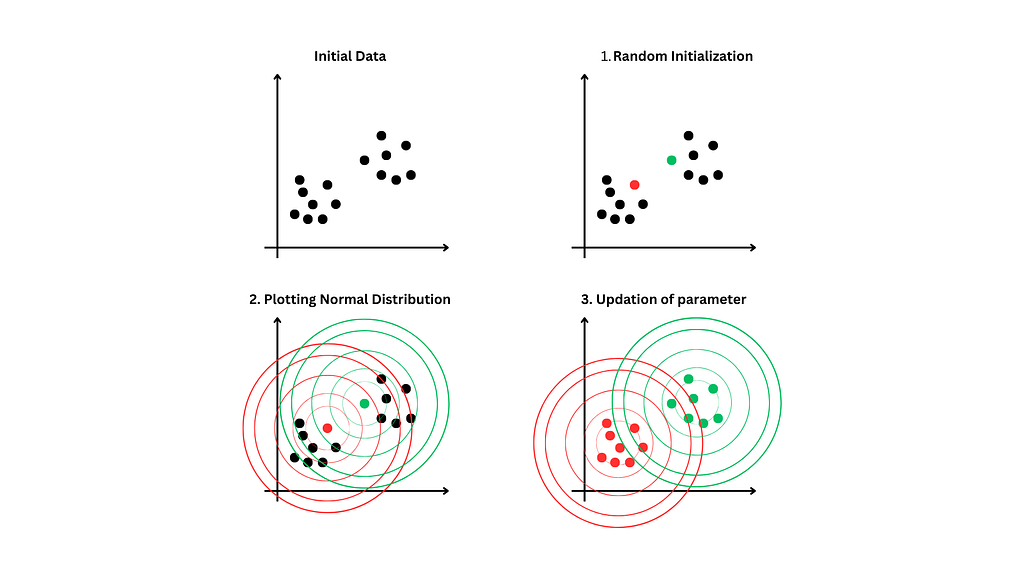
Expectation-Maximization Algorithm
1. Initialization
- Choose the number of components(k) i.e. the number of Gaussian distributions to use in the model.
- Initialize each component's means, covariance, and mixture weights(weights assigned to each distribution).

Repeat the following steps until convergence
2. E-step
calculate responsibility: For each data point X and each distribution K calculate the responsibility.
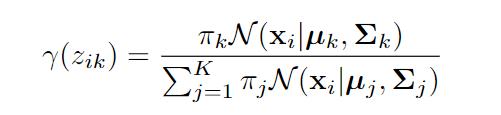
where N(x|μₖ, Σₖ) is the probability density of point Xi under k-th Gaussian distribution.
Responsibility can be understood as Normalized weighted likelihood.It tells us in which distribution a point should belong.

3. M-step
update the parameters for each Gaussian distribution based on the responsibilities calculated in the previous step.
- updating Means: The mean for k-th distribution is calculated as below.
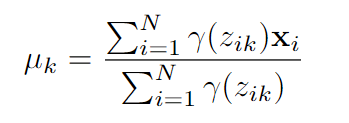
- Updating Covariances: The updated covariance matrix for component k is calculated as
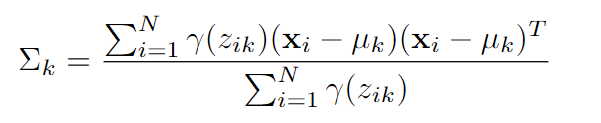
- Updating mixture weights: The weights are updated by the formula given below.
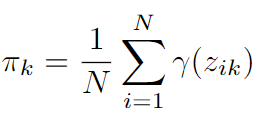


Implementation in python
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture
# Generate the dataset
X, y = make_blobs(n_samples=500, centers=[(0, 0), (4, 4)], random_state=0)
transformation = [[0.6, -0.6], [-0.2, 0.8]]
X = np.dot(X, transformation)
X2, y2 = make_blobs(n_samples=150, centers=[(-2, -2)], cluster_std=0.5, random_state=0)
X = np.vstack((X, X2))
# Fit the GMM model
gmm = GaussianMixture(n_components=3)
labels = gmm.fit_predict(X)
fig, axes = plt.subplots(1,2, figsize=(12, 4))
# Plot the generated data
def plot_data(ax, X):
sns.scatterplot(x=X[:, 0], y=X[:, 1], edgecolor='k', ax=ax)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_title('Generated Data')
plot_data(axes[0], X)
# Plot the GMM clustering results
def plot_clusters(ax, X, labels):
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=labels, palette='tab10', edgecolor='k', ax=ax)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_title('GMM Clustering')
plot_clusters(axes[1], X, labels)
plt.tight_layout()
plt.show()
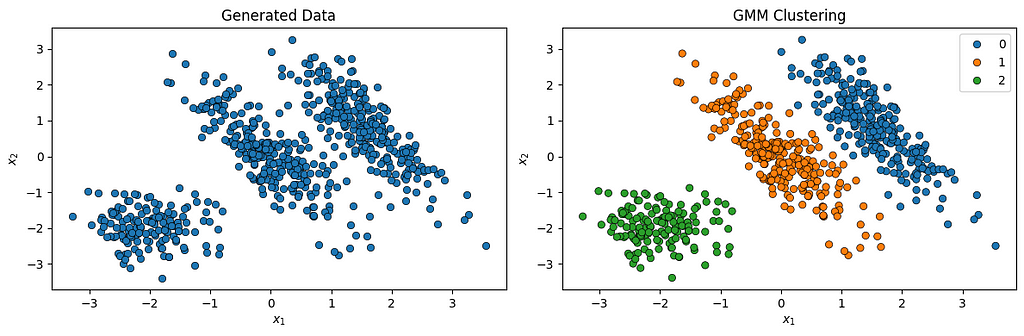
We can check how many iterations it took for the EM algorithm to converge:
print(gmm.n_iter_)
# output :2
We can also examine the estimated GMM parameters:
print('Weights:', gmm.weights_)
print('Means:\n', gmm.means_)
print('Covariances:\n', gmm.covariances_)Weights: [0.38466412 0.38456238 0.2307735 ]
Means:
[[ 1.56399966 0.80290061]
[-0.03258573 0.0352152 ]
[-2.01578797 -1.95661981]]
Covariances:
[[[ 0.35589955 -0.48208467]
[-0.48208467 0.98321962]]
[[ 0.41181801 -0.53087977]
[-0.53087977 0.99972327]]
[[ 0.25431624 -0.01588235]
[-0.01588235 0.24474167]]]
In addition, we can use the method predict_proba() to obtain the membership probabilities for each data point in each cluster.
prob = gmm.predict_proba(X)
array([[9.99999999e-01, 8.40136327e-10, 3.11332827e-21],
[8.57781313e-10, 9.99994173e-01, 5.82656710e-06],
[2.64255409e-06, 9.99997333e-01, 2.46433575e-08],
...,
[2.25955490e-53, 5.16830520e-21, 1.00000000e+00],
[1.30977658e-56, 8.53053556e-23, 1.00000000e+00],
[2.96050654e-51, 8.73008314e-20, 1.00000000e+00]])
probabilities of each data point belonging to the 3 clusters.
Limitations of GMMs
- We are required to specify the number of components (clusters) in advance. This can be challenging if we do not have information about the number of clusters in our data.
- Assume that the data in each cluster follows a Gaussian distribution, which may not accurately represent real-world data.
- May not perform well when clusters contain only a few data points, as the model requires sufficient data to estimate the parameters of each component accurately.
- The clustering results can be sensitive to the initial choice of parameters.
Model-Based Clustering using GMM-Gaussian Mixture Models was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Saarthak Gupta
Saarthak Gupta | Sciencx (2024-07-30T15:01:25+00:00) Model-Based Clustering using GMM-Gaussian Mixture Models. Retrieved from https://www.scien.cx/2024/07/30/model-based-clustering-using-gmm-gaussian-mixture-models/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
