This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
:::info Authors:
(1) Mehdi Naderi;
(2) Markos Papageorgiou;
(3) Dimitrios Troullinos;
(4) Iasson Karafyllis;
(5) Ioannis Papamichail.
:::
Table of Links
The Nonlinear Feedback Control
OD Corridors and Desired Orientations
Boundary and Safety Controllers
Appendix A: Collision Detection
Appendix B: Transformed ISO-Distance curves
Appendix D: Safety Controller Details
Appendix E: Controller Parameters
APPENDIX D: SAFETY CONTROLLER DETAILS
A. Finding cross-point when EV and obstacle have circular and skewed motions, respectively
\ In this case, the cross-point can be found by crossing the following movement equations:
\
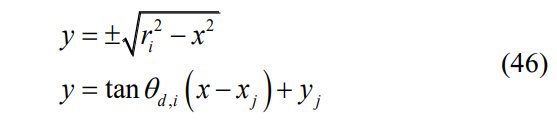
\ So, the cross-point’s longitudinal position is one of the roots of the following second-order polynomial that results from (46) after simplification:
\

\ B. Finding cross-point when EV and obstacle have skewed and circular motions, respectively
\ Following a similar procedure to the previous one, the crosspoint can be found by calculating roots of the following equation:
\
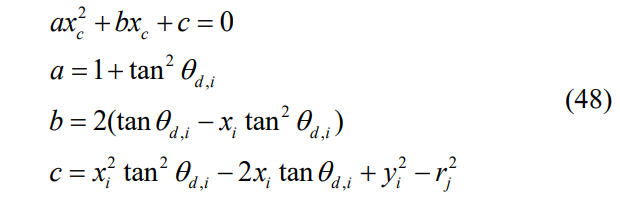
\ The found cross-points should be transformed to the coordinates aligned with the EV’s desired orientation. If they are behind the EV or obstacle or the roots are not real, they are ignored. Otherwise, the closest cross-point is considered.
\ C. Finding the closest current obstacle
\

\
:::info This paper is available on arxiv under CC 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
EScholar: Electronic Academic Papers for Scholars | Sciencx (2024-09-03T13:30:12+00:00) Handling Complex Vehicle Movements: Techniques for Finding Cross-Points and Obstacles. Retrieved from https://www.scien.cx/2024/09/03/handling-complex-vehicle-movements-techniques-for-finding-cross-points-and-obstacles/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
