This content originally appeared on HackerNoon and was authored by Extrapolate
:::info Author:
(1) K. Razi Naqvi, Department of Physics, Norwegian University of Science and Technology (NTNU), 7094 Trondheim, Norway
:::
Table of Links
3 Comments elicited by the solution to Milne’s problem for B-particles
6 Concluding remarks and References
3 Comments elicited by the solution to Milne’s problem for B-particles

\ Far from the wall the density increases linearly with distance, as one expects from the diffusion equation. When this asymptotic solution is extrapolated across the boundary region it reaches zero not at the wall (as the solution of the diffusion equation with absorbing boundary would) but at some distance beyond it. The value we find for this “Milne extrapolation length” is, in the appropriate dimensionless units, approximately twice the value found in the radiative transfer problem. The density in the actual solution is everywhere lower than that of the extrapolated asymptotic solution, but of course it stays finite at the wall.
\

3.1 Length scales for Brownian moton and its inverse

\
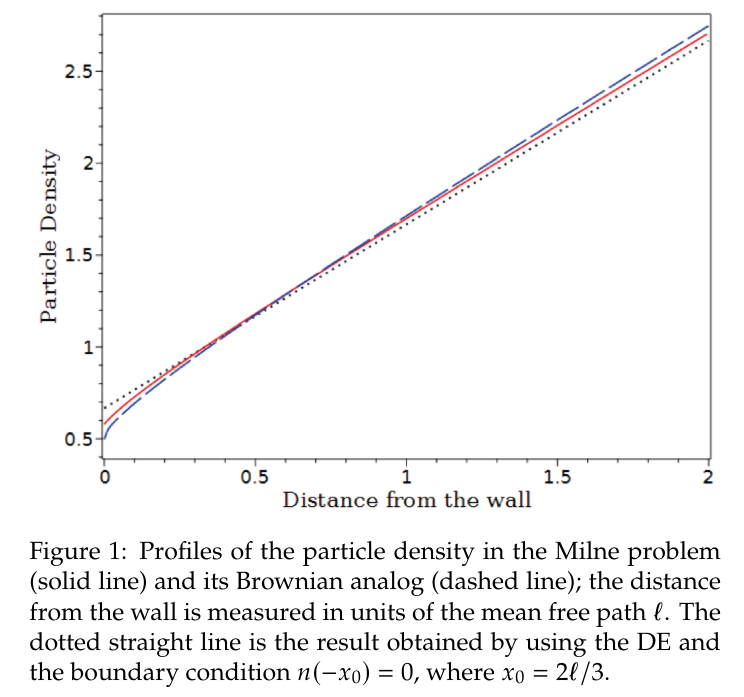
3.2 Profiles of particle density

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Extrapolate
Extrapolate | Sciencx (2024-09-04T13:00:17+00:00) Revisiting Discrepancies in Diffusion Theory: The Solution to Milne’s Problem for B-particles. Retrieved from https://www.scien.cx/2024/09/04/revisiting-discrepancies-in-diffusion-theory-the-solution-to-milnes-problem-for-b-particles/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
