This content originally appeared on HackerNoon and was authored by Cosmological thinking: time, space and universal causation
:::info Authors:
(1) Zhan Ling, UC San Diego and equal contribution;
(2) Yunhao Fang, UC San Diego and equal contribution;
(3) Xuanlin Li, UC San Diego;
(4) Zhiao Huang, UC San Diego;
(5) Mingu Lee, Qualcomm AI Research and Qualcomm AI Research
(6) Roland Memisevic, Qualcomm AI Research;
(7) Hao Su, UC San Diego.
:::
Table of Links
Motivation and Problem Formulation
Deductively Verifiable Chain-of-Thought Reasoning
Conclusion, Acknowledgements and References
\ A Deductive Verification with Vicuna Models
C More Details on Answer Extraction
E More Deductive Verification Examples
3 Motivation and Problem Formulation

\ We observe that for all cases where LLMs produce erroneous final answers, there exists at least one mistake among the intermediate reasoning steps S. Moreover, even when the final answer is correct, there might still exist some mistakes among S. This phenomenon, as illustrated in Tab. 1, occurs for all LLMs we tested, including state-of-the-art models such as ChatGPT and GPT-4 [32]. Since later reasoning steps are conditioned on prior reasoning steps, these mistakes often initiate a snowball effect, causing subsequent mistakes to compound. This significantly diminishes the likelihood of correct problem-solving and impedes the progress towards achieving human-level complex reasoning.
\ Therefore, in this work, we place significant emphasis on ensuring the validity of every reasoning step, not just the correctness of the final answer. In particular, we focus on the validity of deductive reasoning, an essential component of a logical reasoning process. In deductive reasoning, we are
\
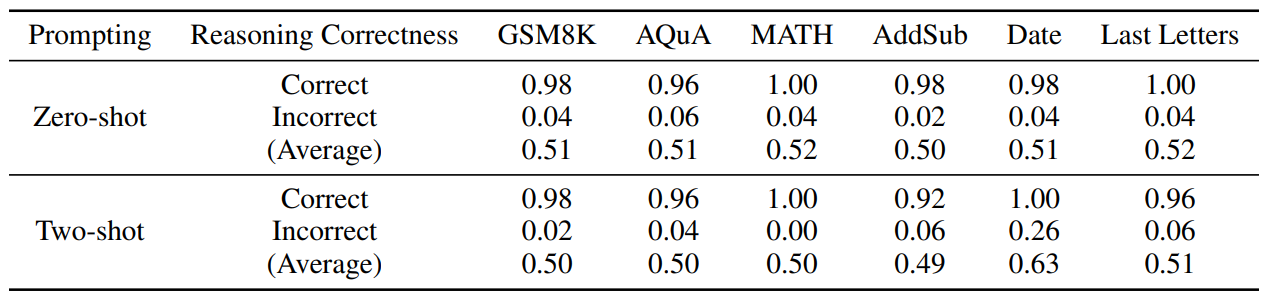
\ given a (premise, conclusion) pair, and we are interested in determining whether the conclusion follows from the premises. In the context of reasoning-based QA tasks, for each reasoning step si , we define its deductive validity V (si) as a binary variable. A reasoning step is deductively valid (V (si) = 1) if and only if si can be logically deduced from its corresponding premises pi , which consist of the context C, the question Q, and all the previous reasoning steps sj (j < i). Then, we can also define the deductive validity for the entire reasoning chain S as V (S) = ∧M i=1V (si). Compared to evaluating answer correctness, which can be accomplished by simple functions such as exact string match, evaluating deductive validity is a lot more challenging. Thanks to the recent progress on LLMs, which demonstrate impressive in-context learning capabilities across diverse scenarios, we propose to use LLMs to examine reasoning chains and predict the deductive reasoning validity.
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Cosmological thinking: time, space and universal causation
Cosmological thinking: time, space and universal causation | Sciencx (2024-09-08T13:58:54+00:00) Breaking Down Deductive Reasoning Errors in LLMs. Retrieved from https://www.scien.cx/2024/09/08/breaking-down-deductive-reasoning-errors-in-llms/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
