This content originally appeared on HackerNoon and was authored by Restructure
:::info Authors:
(1) Oleksandr Kuznetsov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA and Department of Political Sciences, Communication and International Relations, University of Macerata, Via Crescimbeni, 30/32, 62100 Macerata, Italy (kuznetsov@karazin.ua);
(2) Dzianis Kanonik, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(3) Alex Rusnak, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA (alex@proxima.one);
(4) Anton Yezhov, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA;
(5) Oleksandr Domin, Proxima Labs, 1501 Larkin Street, suite 300, San Francisco, USA.
:::
Table of Links
1.1. The Blockchain Paradigm and the Challenge of Scalability
1.3. Our contribution and 1.4. Article structure
2. Conceptualizing the Problem
3. Our Idea for Optimizing Trees in Blockchain
4. Efficiency of adaptive Merkle trees
5. Algorithm for Merkle Tree Restructuring
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping
6.3. Example 2.1: Restructuring a Non-Binary Tree by Adding a Single Leaf
6.4. Example 2.2: Restructuring a Non-Binary Tree Through Leaf Pair Swapping
6.5. Example 2.3: Restructuring a Patricia-Merkle Tree Fragment Through Leaf Pair Swapping
7. Path Encoding in the Adaptive Merkle Tree
8.2. Technology and Advantages
9.2. Comparison with Existing Solutions
6.2. Example 1.1: Binary Tree Restructuring Through Leaf Node Swapping

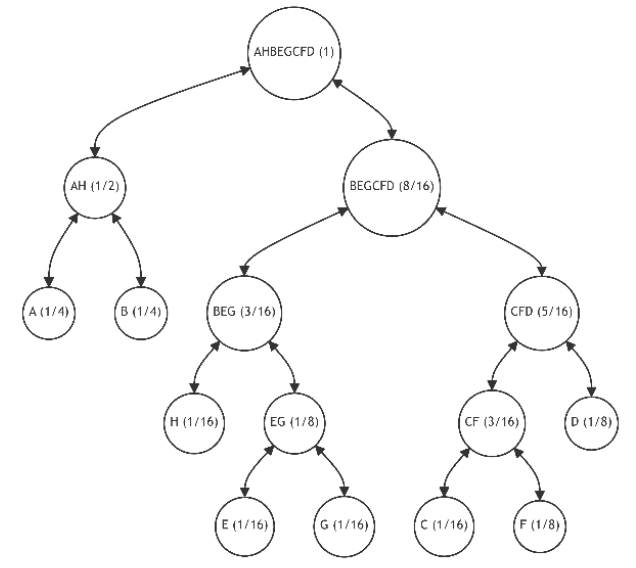
\ Clearly, the best alternative for our example is to swap leaves B and H. Visually, this corresponds to the same graph shown in Figure 16.1 – identical to Figure 16 but with B and H swapped.
\ After this restructuring, we observe the following distribution of elementary discrepancies:
\

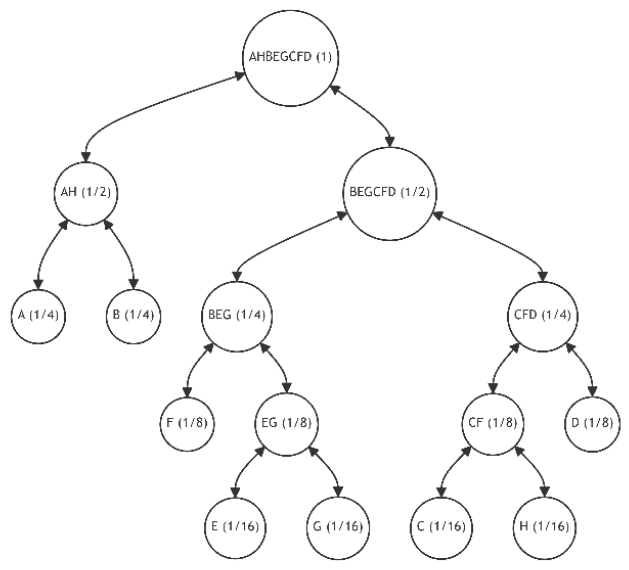
\ Now, the only viable alternative is to swap leaves H and F, which results in a zero average discrepancy, indicating an optimal structure in terms of minimizing the average path length in the binary tree. The outcome of this optimization is depicted in Figure 16.2.
\
\
\ It's important to note that non-binary trees are often used in practical scenarios. For instance, Ethereum's blockchain utilizes a Patricia-Merkle tree, which can have up to 16 child nodes, i.e., m =16.
\ Let's demonstrate the algorithm's operation on a simple example of a non-binary (m = 4 ) tree.
\
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Restructure
Restructure | Sciencx (2024-09-10T23:45:20+00:00) Binary Tree Restructuring Through Leaf Node Swapping. Retrieved from https://www.scien.cx/2024/09/10/binary-tree-restructuring-through-leaf-node-swapping/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
