This content originally appeared on HackerNoon and was authored by Sin7Y
\ Reducing computational complexity has always been one of the primary goals of blockchain technology. One effective approach to achieving this is by reducing the bit width of the computation field. For example, SNARKs based on elliptic curves perform arithmetic operations in fields with bit widths of 256 or higher, while STARKs have evolved from using the 64-bit Goldilocks field to the 31-bit Mersenne31 and BabyBear fields. Beyond the efficiency of the prime numbers during modular operations, the significant reduction in bit width has led to Plonky2 being hundreds of times faster than its predecessor, Plonky. Following this trajectory, one might wonder: is it possible to set the field width to 1, specifically ${\mathbb{F}}_{2}$? The Ulvetanna (IRREDUCIBLE) team addressed this question in their research paper titled Succinct Arguments over Towers of Binary Fields [1], and implemented it in Rust with their project, Binius: a Hardware-Optimized SNARK [2][3].
\ Since its release, Binius has garnered significant attention in the ZK (Zero-Knowledge) community. The LambdaClass team has provided several technical analyses [4][5][6], and Vitalik Buterin offered a more accessible explanation [7]. In this article, we will explore the foundations of Binius, focusing on the Towers of Binary Fields, from both a technical and implementation perspective.
Binary Fields
The implementation of Binius is based on Binary Fields. In Binius, Binary Fields are constructed using towers of field extensions.
\
The simplest Binary Field is ${{\mathbb{F}}{2}}$, which contains only two elements ${0,1}$, with operations performed modulo 2: addition corresponds to bitwise XOR, and multiplication corresponds to bitwise AND. By choosing an irreducible polynomial $m(x) = x^{2} + x + 1$ over ${{\mathbb{F}}{2}}$, we can form the field ${{\mathbb{F}}_{{2^{2}}}}$, where the elements are remainders of polynomials of degree at most 1, $r(x) = ax + b$ (with $a, b \in {0, 1}$).
\ While one method to extend fields involves taking remainders using irreducible polynomials, Binius employs a more efficient approach: the use of Multilinear Lagrange polynomials as a basis for tower extensions. This method allows for recursive field extensions, where each extension field is nested within the previous one.
\
The Specific Implementation of Tower Extensions is as Follows: First, ${{\tau }{0}} = {{\mathbb{F}}{2}}$; Then, ${{\tau }{1}} = \frac{{{\mathbb{F}}{2}}[{{x}{0}}]}{(x{0}^{2} + {{x}_{0}} + 1)}$; Next, ${{\tau }{k}} = \frac{{{\mathbb{F}}{2}}[{{x}{k-1}}]}{(x{k-1}^{2} + {{x}{k-1}}{{x}{k-2}} + 1)}$.
\
From the construction process of the field extensions, it is clear that the extensions satisfy the following relationship: ${{\tau }{0}} \subset {{\tau }{1}} \subset {{\tau }{2}} \subset \cdots \subset {{\tau }{m}}$. For $k \ge 0$, the field extension can also be expressed in the direct form of a ring as: ${{\tau }{k}}={{{\mathbb{F}}{2}}[{{x}{0,}}\ldots ,{{x}{k-1}}]}/{\left( x_{0}^{2}+{{x}{0}}+1,\ldots ,x{k-1}^{2}+{{x}{k-2}}{{x}{k-1}}+1 \right)}$.
\ Based on this implementation, different extensions can be obtained as follows:
\
${{\tau }_{0}}=\left{ 0,1 \right}$\
${{\tau }{1}}=\left{ 0+0{{x}{0}},1+0{{x}{0}},0+1{{x}{0}},1+1{{x}{0}} \right}$, or ${{\tau }{1}}=\left{ {{\tau }{0}},0+1{{x}{0}},1+1{{x}_{0}} \right}$\
$${{\tau }{2}}=\left{ \begin{align} & 0+0{{x}{0}}+0{{x}{1}}+0{{x}{0}}{{x}{1}},1+0{{x}{0}}+0{{x}{1}}+0{{x}{0}}{{x}{1}},0+1{{x}{0}}+0{{x}{1}}+0{{x}{0}}{{x}{1}}, \ & 1+1{{x}{0}}+0{{x}{1}}+0{{x}{0}}{{x}{1}},\ldots ,1+1{{x}{0}}+1{{x}{1}}+1{{x}{0}}x \ \end{align} \right}$$, Or ${{\tau }{2}}=\left{ {{\tau }{1}},0+0{{x}{0}}+1{{x}{1}}+0{{x}{0}}{{x}{1}},\ldots ,1+1{{x}{0}}+1{{x}{1}}+1{{x}{0}}{{x}{1}} \right}$
\
From the Elements Contained in the Extended Field It is evident that for an element ${{b}{0}}{{b}{1}}{{b}{2}}\ldots {{b}{{{2}^{k}}-1}}$ derived from ${{\tau }{k}}$, it can be decomposed into the sum of two parts: ${{b}{lo}} + {{x}{k-1}}{{b}{hi}}$ (where ${{b}{lo}}, {{b}{hi}} \in {{\tau }{k-1}}$). For example, $1100101010001111 = 11001010 + 1000111 \times {{x}{3}}$, where $11001010, 10001111 \in {{\tau }{2}}$.
\
By iteratively decomposing, we can finally express: $$1100101010001111=1+{{x}{0}}+{{x}{2}}+{{x}{2}}{{x}{1}}+{{x}{3}}+{{x}{2}}{{x}{3}}+{{x}{0}}{{x}{2}}{{x}{3}}+{{x}{1}}{{x}{2}}{{x}{3}}+{{x}{0}}{{x}{1}}{{x}{2}}{{x}{3}}$$
\
Additionally, for $k > 0$, since $x_{k}^{2} = {{x}{k}}{{x}{k-1}} + 1$, addition and multiplication can be efficiently implemented in the binary extended field.
Implementation of Binary Fields
Irreducible provides the open-source Rust implementation of Binius [3]. The source code includes complete implementations and operations for the Tower of Binary Fields [8,9,10].
\
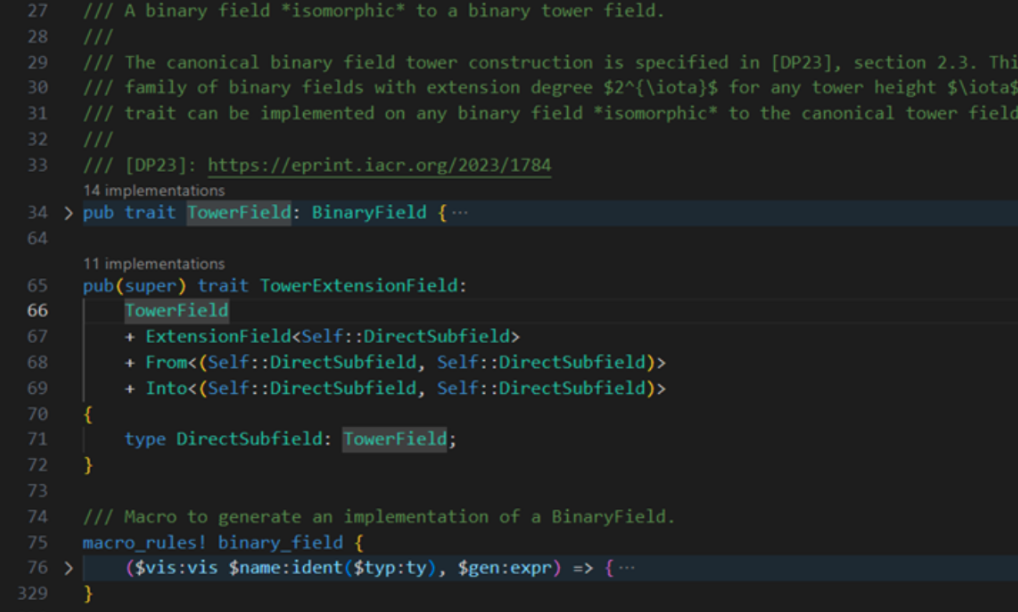
\ In [8], as shown in Figure 1, the implementation includes the complete definition of operations for binary fields and the construction of the Tower of Binary Fields. The Tower of Binary Fields, supporting up to a 128-bit binary field, is defined as follows:
\
\
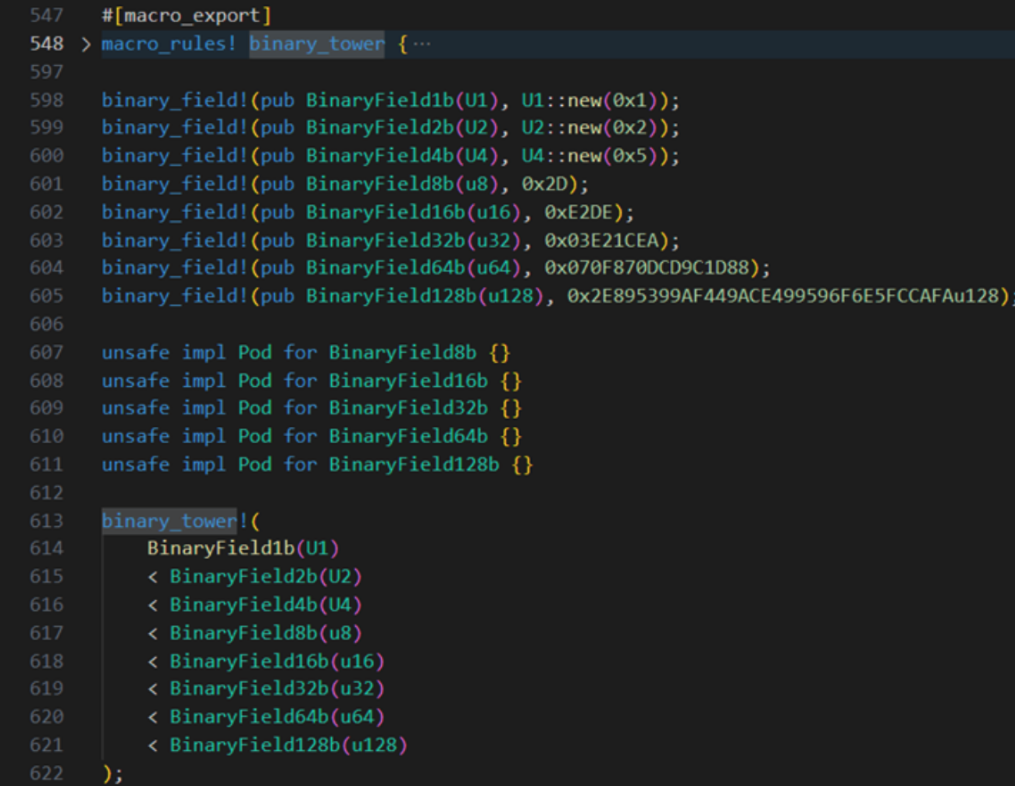
\ Additionally, [8] provides test and verification code for the Tower of Binary Fields and related operations.
References
[1] https://eprint.iacr.org/2023/1784
[2] https://www.irreducible.com/posts/binius-hardware-optimized-snark
[3] https://gitlab.com/IrreducibleOSS/binius
[4] SNARKs on binary fields: Binius - Part 1 (lambdaclass.com)
[5] SNARKs on binary fields: Binius - Part 2 (lambdaclass.com)
[6] How Binius is helping move the ZK industry forward (lambdaclass.com)
[7] https://vitalik.eth.limo/general/2024/04/29/binius.html
[8] binius/crates/field/src/binary_field.rs at main · IrreducibleOSS/binius · GitHub
[9] binius/crates/field/src/binaryfieldarithmetic.rs at main · IrreducibleOSS/binius · GitHub
[10] binius/crates/field/src/extension.rs at main · IrreducibleOSS/binius · GitHub
This content originally appeared on HackerNoon and was authored by Sin7Y
Sin7Y | Sciencx (2024-09-13T13:23:19+00:00) How Binius Reduces Computational Complexity with Towers of Binary Fields. Retrieved from https://www.scien.cx/2024/09/13/how-binius-reduces-computational-complexity-with-towers-of-binary-fields/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
