This content originally appeared on HackerNoon and was authored by Neeraj Choubisa
Automated Market Makers (AMMs) are essential to the decentralized finance (DeFi) ecosystem because they facilitate trading and liquidity provision. The Constant Product AMM, which powers well-known decentralized exchanges like Uniswap and SushiSwap, is a fundamental idea in this field.
\ In this blog, we'll examine the ==Constant Product Automated Market Maker== and explore the arithmetic involved in introducing and withdrawing liquidity.
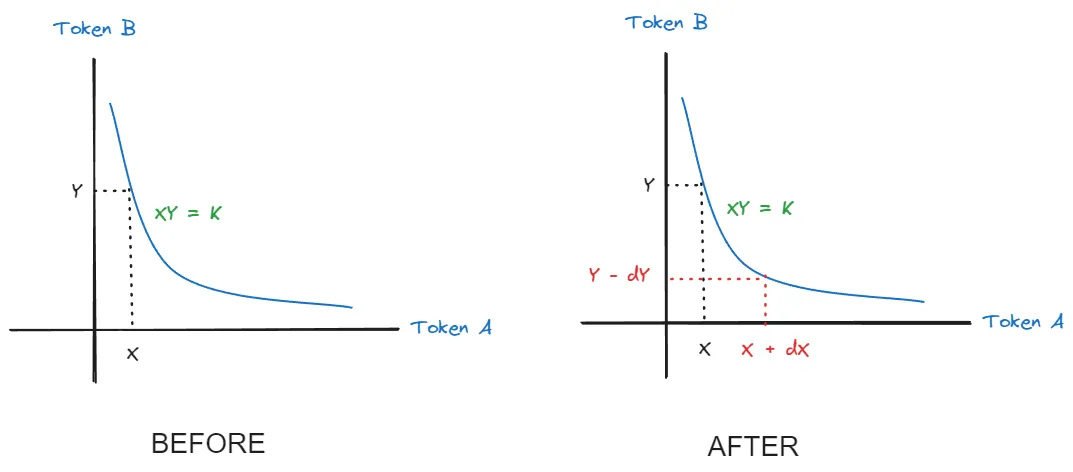
\ The basic principle behind Constant AMM is the constant product formula, which ensures that the product of the quantities of two tokens in the pool remains constant.
Working Principle
The Constant AMM works on the following equation:
x * y = k
\ Where:
xrepresents the quantity of Token A in the liquidity pool(CPAMM).yrepresents the quantity of Token B in the liquidity pool(CPAMM).kis a constant value that remains unchanged during swaps (until liquidity is added or removed).CPAMM:Constant Product Automated Market Maker
\
This means that when a trade is executed, the quantities of x and y adjust in a way that the product of the two still equals k. The constant product formula prevents the price from being easily manipulated because large trades significantly affect the token price.
\ Let's Understand this Formula with the help of one Real-life Example :grinning: :
Step-by-Step Example
Assume the liquidity pool contains the following:
- 100 units of Token A
- 200 units of Token B
\ Then, the constant product is:
100 * 200 = 20,000
\ This means that, no matter how many tokens are swapped, the product of the amount of Token A and Token B in the pool must always equal 20,000 (unless liquidity is added or removed).
\ Now, let’s say a trader wants to buy 10 units of Token A. To execute this trade, they need to deposit some amount of Token B into the pool in exchange for the 10 units of Token A they wish to acquire.
\
After the trade, the pool must still satisfy the constant product formula (x * y = k), so the quantities of Token A and Token B in the pool must be adjusted accordingly.
Calculating the New Amounts in the Pool
- Before the trade, there were 100 units of Token A.
- After the trade, the trader will take 10 units of Token A, so there will be 90 units of Token A left in the pool.
\
Let’s represent the new amount of Token B as y'. We now use the constant product formula to find the new amount of Token B:
x' * y' = k
\ Where:
x' = 90(the new amount of Token A in the pool after the trade)k = 20,000(the constant value from the initial state)y'is the new amount of Token B we need to calculate.
\
90 * y' = 20,000
y' = 20,000 / 90
y' ≈ 222.22
\
So, after the trade, there will be 222.22 units of Token B in the pool.
\
Calculating How Much Token B the Trader Needs to Pay
Before the trade, the pool contained 200 units of Token B. After the trade, there will be 222.22 units of Token B in the pool. The trader needs to deposit the difference, which is:
Amount of Token B to deposit = 222.22 - 200 = 22.22 units
\ So, to buy 10 units of Token A, the trader needs to deposit 22.22 units of Token B into the pool.
\
\ Let's turn this incredible constant product equation into a smart contract and deploy it on (Rootstock) for efficient testing and lightning-fast transactions! This will allow us to leverage RSK's secure and scalable network while exploring the power of decentralized automated market-making.
Prerequisites
You will need the following tools installed to build along with me:
Node.js
NPM
Git Bash
MetaMask
Solidity
Hardhat
Steps to add Rootstock Testnet Details in Metamask
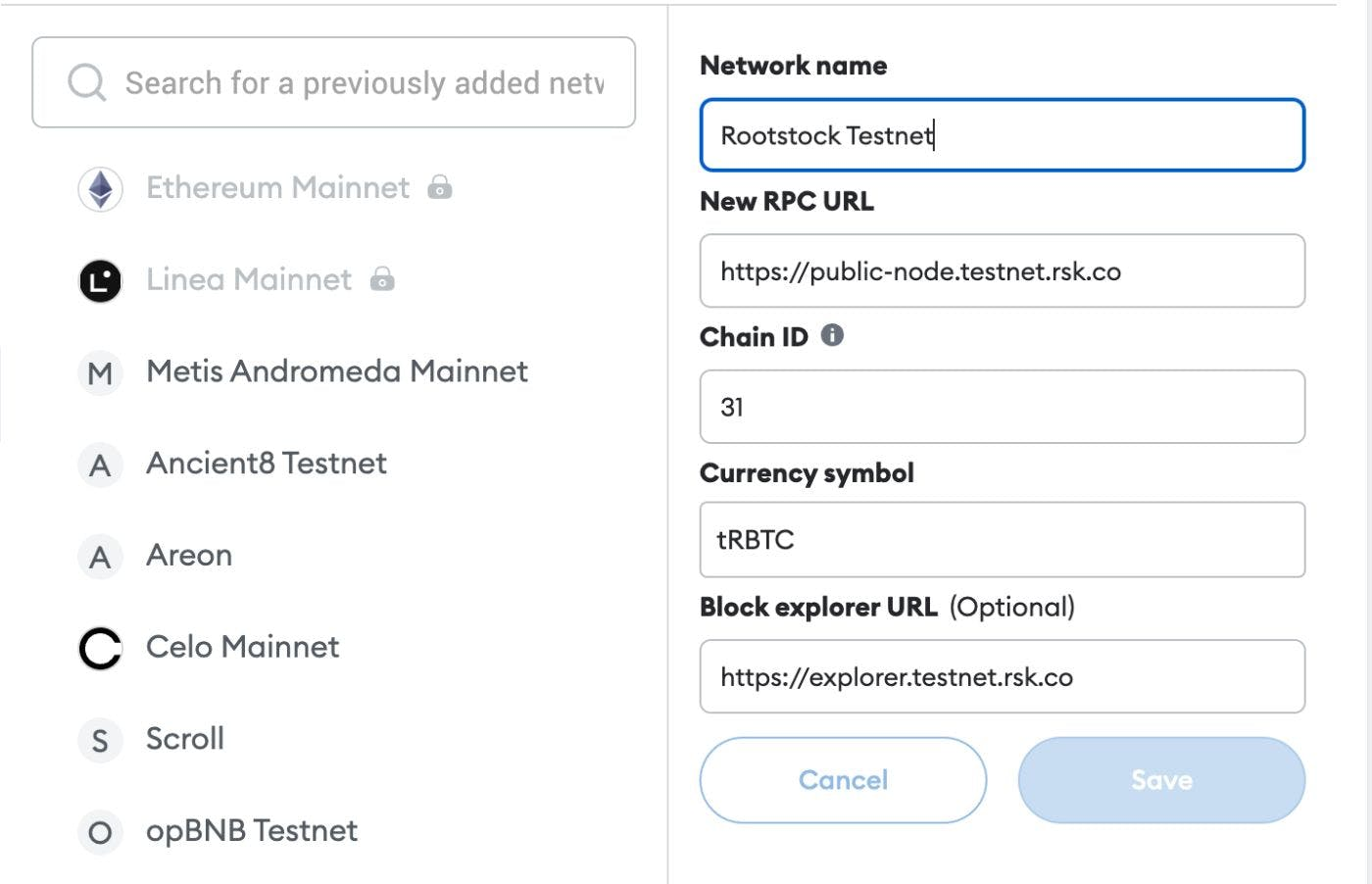
Open the MetaMask Chrome extension
In the network options, choose
custom RPCEnter RSK Testnet as the Network Name
Enter https://public-node.testnet.rsk.co as the RPC URL
Enter RBTC as SymbolPut and Save
Copy the account address
Get the Faucet (tRBTC) from: https://faucet.testnet.rsk.co/
\
\n Setup for Smart Contract Development
Next, we'll develop the smart contract for our platform:
mkdir constant-product-ammcd constant-product-ammnpx hardhat init\
It will set an empty hardhat project now we are good to go … 🏃
\ update the hardhat.config.ts file with the ==rootstock configuration== mentioned below
import "dotenv/config";
import "@nomicfoundation/hardhat-toolbox";
import "@nomicfoundation/hardhat-verify";
const ACCOUNTS = process.env.DEPLOYER_ACCOUNT_PRIV_KEY
? [`${process.env.DEPLOYER_ACCOUNT_PRIV_KEY}`]
: [];
module.exports = {
defaultNetwork: "hardhat",
gasReporter: {
enabled: false,
},
networks: {
hardhat: { chainId: 31337 },
rootstock: {
chainId: 31,
url: "https://public-node.testnet.rsk.co",
accounts: ACCOUNTS,
}
},
etherscan: {
apiKey: {
rootstock: "xxxx-xxx-xx-xx-xxxxx",
},
customChains: [],
},
sourcify: {
enabled: false,
},
solidity: {
version: "0.8.22",
settings: {
evmVersion: "paris",
optimizer: {
enabled: true,
runs: 200,
},
},
},
paths: {
sources: "./contracts",
tests: "./test",
cache: "./cache",
artifacts: "./artifacts",
},
};
\
Now, in the contracts folder, create interfaces and utils subfolders to organize the code structure efficiently. The interfaces folder will hold the contract interfaces, while the utils folder will store utility functions and helper contracts.
\
Then contracts/interfaces add this file IERC20.sol
\
// SPDX-License-Identifier: GPL-3.0
pragma solidity ^0.8.16;
interface IERC20 {
function totalSupply() external view returns (uint256);
function balanceOf(address account) external view returns (uint256);
function decimals() external view returns (uint8);
function allowance(
address owner,
address spender
) external view returns (uint256);
function transfer(
address recipient,
uint256 amount
) external returns (bool);
function approve(address spender, uint256 amount) external returns (bool);
function transferFrom(
address sender,
address recipient,
uint256 amount
) external returns (bool);
event Transfer(address indexed from, address indexed to, uint256 value);
event Approval(
address indexed owner,
address indexed spender,
uint256 value
);
}
\
Now in contracts/utils add this file ERC20.sol
// SPDX-License-Identifier: GPL-3.0
pragma solidity ^0.8.16;
import "@openzeppelin/contracts/token/ERC20/ERC20.sol";
import "@openzeppelin/contracts/access/AccessControl.sol";
contract TestToken is ERC20, AccessControl {
bytes32 public constant MINTER_ROLE = keccak256("MINTER_ROLE");
constructor() ERC20("TestToken", "TestToken") {
_grantRole(DEFAULT_ADMIN_ROLE, msg.sender);
_grantRole(MINTER_ROLE, msg.sender);
}
function mint(address to, uint256 amount) public onlyRole(MINTER_ROLE){
_mint(to, amount);
}
}
\
Now that we've completed the interfaces and utils folders with the essential contracts, it's time to implement the Constant Product Automated Market Maker (AMM) contract. Let's dive into building this!
\
In the Constant Product Automated Market Maker (AMM) contract, we have three key functions: addLiquidity, removeLiquidity, and swap.
\ Let’s go through each function and its code in detail:
\
function addLiquidity(
uint _amount0,
uint _amount1
) external returns (uint shares) {
token0.transferFrom(msg.sender, address(this), _amount0);
token1.transferFrom(msg.sender, address(this), _amount1);
if (reserve0 > 0 || reserve1 > 0) {
require(
reserve0 * _amount1 == reserve1 * _amount0,
"x / y != dx / dy"
);
}
if (totalSupply == 0) {
shares = _sqrt(_amount0 * _amount1);
} else {
shares = _min(
(_amount0 * totalSupply) / reserve0,
(_amount1 * totalSupply) / reserve1
);
}
require(shares > 0, "shares = 0");
_mint(msg.sender, shares);
_update(
token0.balanceOf(address(this)),
token1.balanceOf(address(this))
);
}
\
The addLiquidity function allows a user to deposit two tokens into the pool, ensuring their ratio remains consistent with the existing reserves. It mints liquidity provider (LP) tokens based on the user's share and updates the pool's reserves accordingly. If it's the first deposit, the user's shares are calculated using the square root of the product of the token amounts.
\
function removeLiquidity(
uint _shares
) external returns (uint amount0, uint amount1) {
uint bal0 = token0.balanceOf(address(this));
uint bal1 = token1.balanceOf(address(this));
amount0 = (_shares * bal0) / totalSupply;
amount1 = (_shares * bal1) / totalSupply;
require(amount0 > 0 && amount1 > 0, "amount0 or amount1 = 0");
_burn(msg.sender, _shares);
_update(bal0 - amount0, bal1 - amount1);
token0.transfer(msg.sender, amount0);
token1.transfer(msg.sender, amount1);
}
\
The removeLiquidity function allows a user to withdraw their share of liquidity from the pool. Based on the user's shares, it calculates the amounts of token0 and token1 to return. The function then burns the user's LP tokens, updates the pool's reserves, and transfers the calculated amounts of token0 and token1 back to the user.
\
function swap(
address _tokenIn,
uint _amountIn
) external returns (uint amountOut) {
require(
_tokenIn == address(token0) || _tokenIn == address(token1),
"invalid token"
);
require(_amountIn > 0, "amount in = 0");
bool isToken0 = _tokenIn == address(token0);
(
IERC20 tokenIn,
IERC20 tokenOut,
uint reserveIn,
uint reserveOut
) = isToken0
? (token0, token1, reserve0, reserve1)
: (token1, token0, reserve1, reserve0);
tokenIn.transferFrom(msg.sender, address(this), _amountIn);
// 0.3% fee
uint amountInWithFee = (_amountIn * 997) / 1000;
amountOut =
(reserveOut * amountInWithFee) /
(reserveIn + amountInWithFee);
tokenOut.transfer(msg.sender, amountOut);
_update(
token0.balanceOf(address(this)),
token1.balanceOf(address(this))
);
}
\
The swap function allows users to exchange one token for another in the liquidity pool. It checks if the input token is valid (token0 or token1) and ensures the amount is greater than zero. Based on the input token, it calculates the output amount using the constant product formula with a 0.3% fee. The function then transfers the input token from the user to the pool and sends the corresponding output token back to the user. Finally, it updates the reserves to reflect the new balances after the swap.
\ These are the three main functions of the Constant Product AMM smart contract. Here is full contract
contracts/ConstantProductAMM.sol
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.20;
import {IERC20} from "./interfaces/IERC20.sol";
/**
* @title Constant Product AMM
* @dev A simple implementation of a constant product AMM
*/
contract ConstantProductAMM {
IERC20 public immutable token0;
IERC20 public immutable token1;
uint public reserve0;
uint public reserve1;
uint public totalSupply;
mapping(address => uint) public balanceOf;
constructor(address _token0, address _token1) {
token0 = IERC20(_token0);
token1 = IERC20(_token1);
}
/**
* @dev swap tokens in the AMM
* @param _tokenIn The token to swap in
* @param _amountIn The amount of token to swap in
* @return amountOut The amount of token to receive
*/
function swap(
address _tokenIn,
uint _amountIn
) external returns (uint amountOut) {
require(
_tokenIn == address(token0) || _tokenIn == address(token1),
"invalid token"
);
require(_amountIn > 0, "amount in = 0");
bool isToken0 = _tokenIn == address(token0);
(
IERC20 tokenIn,
IERC20 tokenOut,
uint reserveIn,
uint reserveOut
) = isToken0
? (token0, token1, reserve0, reserve1)
: (token1, token0, reserve1, reserve0);
tokenIn.transferFrom(msg.sender, address(this), _amountIn);
uint amountInWithFee = (_amountIn * 997) / 1000;
amountOut =
(reserveOut * amountInWithFee) /
(reserveIn + amountInWithFee);
tokenOut.transfer(msg.sender, amountOut);
_update(
token0.balanceOf(address(this)),
token1.balanceOf(address(this))
);
}
/**
* @dev add liquidity to the AMM
* @param _amount0 The amount of token0 to add
* @param _amount1 The amount of token1 to add
* @return shares The number of shares minted
*/
function addLiquidity(
uint _amount0,
uint _amount1
) external returns (uint shares) {
token0.transferFrom(msg.sender, address(this), _amount0);
token1.transferFrom(msg.sender, address(this), _amount1);
if (reserve0 > 0 || reserve1 > 0) {
require(
reserve0 * _amount1 == reserve1 * _amount0,
"x / y != dx / dy"
);
}
if (totalSupply == 0) {
shares = _sqrt(_amount0 * _amount1);
} else {
shares = _min(
(_amount0 * totalSupply) / reserve0,
(_amount1 * totalSupply) / reserve1
);
}
require(shares > 0, "shares = 0");
_mint(msg.sender, shares);
_update(
token0.balanceOf(address(this)),
token1.balanceOf(address(this))
);
}
/**
* @dev Remove liquidity from the AMM
* @param _shares The number of shares to remove
* @return amount0 The amount of token0 to receive
* @return amount1 The amount of token1 to receive
*/
function removeLiquidity(
uint _shares
) external returns (uint amount0, uint amount1) {
uint bal0 = token0.balanceOf(address(this));
uint bal1 = token1.balanceOf(address(this));
amount0 = (_shares * bal0) / totalSupply;
amount1 = (_shares * bal1) / totalSupply;
require(amount0 > 0 && amount1 > 0, "amount0 or amount1 = 0");
_burn(msg.sender, _shares);
_update(bal0 - amount0, bal1 - amount1);
token0.transfer(msg.sender, amount0);
token1.transfer(msg.sender, amount1);
}
/**
* @dev Compute square root of a number
* @param y The number to compute the square root of
* @return z The square root of y
*/
function _sqrt(uint y) private pure returns (uint z) {
if (y > 3) {
z = y;
uint x = y / 2 + 1;
while (x < z) {
z = x;
x = (y / x + x) / 2;
}
} else if (y != 0) {
z = 1;
}
}
/**
* @dev Compute the minimum of two numbers
* @param x The first number
* @param y The second number
* @return The minimum of x and y
*/
function _min(uint x, uint y) private pure returns (uint) {
return x <= y ? x : y;
}
function _mint(address _to, uint _amount) private {
balanceOf[_to] += _amount;
totalSupply += _amount;
}
function _burn(address _from, uint _amount) private {
balanceOf[_from] -= _amount;
totalSupply -= _amount;
}
function _update(uint _reserve0, uint _reserve1) private {
reserve0 = _reserve0;
reserve1 = _reserve1;
}
}
\
Deployment on RSK Network
To deploy the Constant Product AMM contract on the RSK network, follow these steps:
- Deploy Token Contracts: First, deploy two token contracts,
TokenAandTokenB. These contracts represent the tokens that will be used in the liquidity pool. - Deploy the Constant Product Pool Contract: After deploying the token contracts, pass the addresses of
TokenAandTokenBto theConstantProductPoolcontract and deploy it. - Below are mentioned Deploy Scripts
\
scripts/deploy_erc20.ts
import { ethers } from 'hardhat'
const ERC20_CONTRACT_NAME = 'TokenB'
async function deployERC20() {
const contractOwner: string = await ethers.getSigners().then((res) => res[0].address)
const myERC20Contract = await ethers.deployContract(ERC20_CONTRACT_NAME);
await myERC20Contract.waitForDeployment()
console.log('Deployed TokenA contract address:', await myERC20Contract.getAddress())
}
async function main() {
await deployERC20();
}
main().catch((error) => {
console.error(error)
process.exit(1)
})
\
scripts/deploy_constant_product_pool.ts
import { ethers } from 'hardhat'
const ConstantProductAMM_Contract_Name = 'ConstantProductAMM'
const tokenA="0xbC3E6978e86cBE779E820784ff703bC0851CdFF1";
const tokenB="0xB6E01FE5184Bd310802B33461660BD12dF0b20F2";
async function deployERC20() {
const contractOwner: string = await ethers.getSigners().then((res) => res[0].address)
const constantProductContract = await ethers.deployContract(ConstantProductAMM_Contract_Name,[
tokenA,
tokenB
]);
await constantProductContract.waitForDeployment()
console.log('Deployed Constant Product AMM contract address:', await constantProductContract.getAddress())
}
async function main() {
await deployERC20();
}
main().catch((error) => {
console.error(error)
process.exit(1)
})
\ Now Deploy TokenA :
npx hardhat run scripts/deploy_erc20.ts --network rootstock

Now Deploy TokenB :
npx hardhat run scripts/deploy_erc20.ts --network rootstock

Let’s Finally Deploy Constant Product Automated Market Maker :
npx hardhat run scripts/deploy_constant_product_pool.ts --network rootstock

\ \ \
Conclusion
The Constant AMM offers an effective and decentralized way to trade tokens using a straightforward mathematical formula, ensuring ongoing liquidity and a seamless trading experience without the need for traditional market makers.
\ In this tutorial, we explored how to create a constant product contract, understood the underlying mathematics, and learned how to deploy it on the RSK network using Hardhat and deployment scripts.
\ If you have any questions or wish to contribute, please feel free to open a pull request, report issues, and explore the repository. If you find it useful, don't forget to give it a star! ⭐️
\ Happy coding!
This content originally appeared on HackerNoon and was authored by Neeraj Choubisa
Neeraj Choubisa | Sciencx (2024-09-16T17:05:52+00:00) Constant Product Automated Market Maker: On Rootstock. Retrieved from https://www.scien.cx/2024/09/16/constant-product-automated-market-maker-on-rootstock/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
