This content originally appeared on HackerNoon and was authored by Gamifications
:::info Authors:
(1) Chengfeng Shen, School of Mathematical Sciences, Peking University, Beijing;
(2) Yifan Luo, School of Mathematical Sciences, Peking University, Beijing;
(3) Zhennan Zhou, Beijing International Center for Mathematical Research, Peking University.
:::
Table of Links
2 Model and 2.1 Optimal Stopping and Obstacle Problem
2.2 Mean Field Games with Optimal Stopping
2.3 Pure Strategy Equilibrium for OSMFG
2.4 Mixed Strategy Equilibrium for OSMFG
3 Algorithm Construction and 3.1 Fictitious Play
3.2 Convergence of Fictitious Play to Mixed Strategy Equilibrium
3.3 Algorithm Based on Fictitious Play
4 Numerical Experiments and 4.1 A Non-local OSMFG Example
5 Conclusion, Acknowledgement, and References
3.4 Numerical Analysis
In this part, our goal is to prove the convergence of algorithm 2 when implicit scheme (3.25) and (3.26) are applied. The convergence analysis mirrors the proof for Theorem 3.1, requiring only adapting the arguments to a discretized version.
\

\ Definition 3.4 (implicit discretized system for mixed strategy equilibrium) We define
\

\ the complementary condition
\

\ will be weaker than the following one
\

\
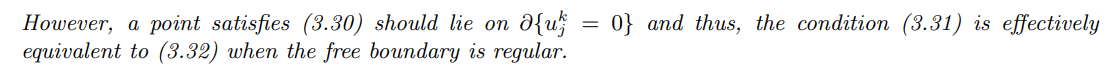
\ Before stating the main result, we present a property of the implicit scheme for obstacle equations: the discretized solution u continuously depends on the discretized source term f.
\ Lemma 3.1 Consider the following discrete obstacle problem:
\

\ Now we can state the main convergence result in this section.
\

\ Proof The spirit of the proof is analog to the one in theorem 3.1. We divide the proof into 3 steps just parallel to the proof of theorem 3.1.
\

\ with equality if and only if
\
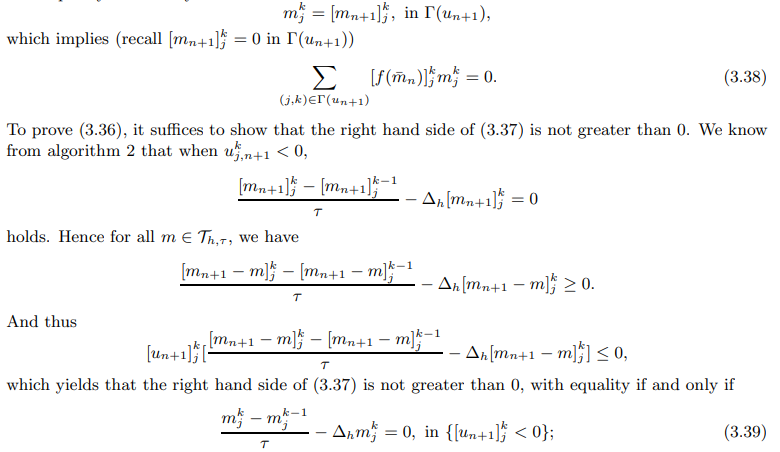
\
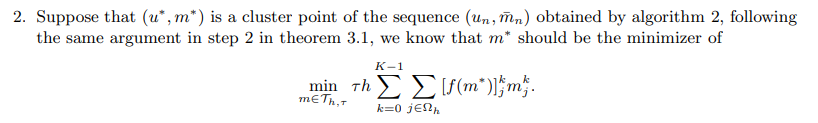
\ 3. We conclude that any cluster point (u∗, m∗) is a solution to (3.29). We first verify that u∗ will satisfy the discretized obstacle problem as follows:
\

\
:::info This paper is available on arxiv under CC 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Gamifications
Gamifications | Sciencx (2024-09-25T19:00:26+00:00) Fictitious Play for Mixed Strategy Equilibria in Mean Field Games: Numerical Analysis. Retrieved from https://www.scien.cx/2024/09/25/fictitious-play-for-mixed-strategy-equilibria-in-mean-field-games-numerical-analysis/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
