This content originally appeared on HackerNoon and was authored by Vibhas Mohan Zanpure
Introduction
Bloom filters are a space-efficient probabilistic data structure used to test whether an ‘element’ is part of a Set. Developed by Burton Howard Bloom in 1970, they offer an effective solution for membership queries, enabling fast and memory-efficient operations. Unlike traditional deterministic data structures like hash tables or binary search trees, Bloom filters are a probabilistic data structure that sacrifices accuracy for performance and space savings. You may think, why should I use a data structure that is not accurate, instead of, lets say, a hash table? As we will see later, there are actually good use cases for it. This article delves into the mechanics, applications, and limitations of Bloom filters, providing a comprehensive understanding of how they work and where they can be best applied.
How Bloom Filters Work
A Bloom filter is essentially an array of ‘m’ bits, all initially set to zero, combined with a set of ‘k’ independent hash functions. When an element is added to the filter, it is processed by each of these hash functions, each producing an index in the array. The corresponding bits at these indices are set to one. To check if an element is in the set, it is hashed again using the same ‘k’ functions, and the bits at the resulting indices are checked. If all bits are set to one, the element is assumed to be in the set, although there is a possibility of a false positive. If any bit is zero, the element is definitely not in the set. Consequently, Bloom Filters can accurately predict when an element is not a member of a set, but they cannot accurately predict if an element is a member of the set.
\ As we can see in below diagram, if we add strings “Alice” and “Bob” using two hash functions in an array of size 10, it results into 1st, 3rd, 4th and 6th indices in the array set to 1. If we want to see if “Alice” is in the set, we can again run through the same hash functions, and check if 1st and 4th indices in the array are set to 1. In this case they are, so we can say that Alice “may be” was added to the array earlier. We cannot say with 100% accuracy, as the bits may have been set for some other string earlier. For example, as we can see, “Charlie” was never added to the set, but because 4th and 6th indices are set to 1, the bloom filter’s set membership check returns true, which is a false positive. In the next section, we take a look at what governs the false positive rate for a bloom filter and what tradeoffs are applicable.
\
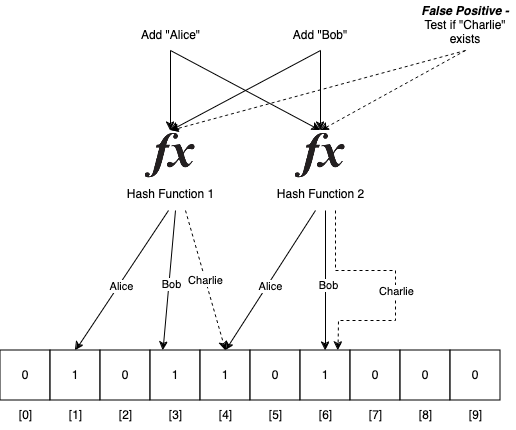
\
Mathematical Foundation
The probability of a false positive, p, in a Bloom filter can be calculated as:
\
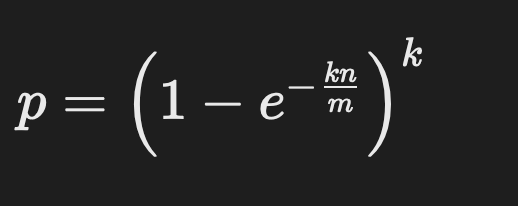
\ Where:
- k is the number of hash functions,
- n is the number of elements in the set,
- m is the number of bits in the filter.
Optimizing a Bloom filter involves choosing the right values for k and m. The optimal number of hash functions, k, is given by:
\
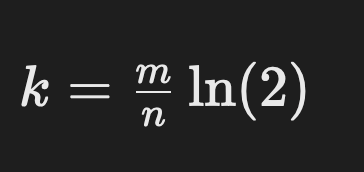
\ This minimizes the false positive rate, balancing between the size of the bit array and the number of hash functions used.
\
Applications of Bloom Filters
- Database and Caching Systems: Bloom filters are often used in database systems to speed up query operations. For instance, a database cache can use a Bloom filter to quickly determine if a query result is likely already in the cache, thus avoiding a potentially expensive database lookup.
- Networking and Security: In network applications, Bloom filters are used for packet routing and spam filtering. They help in checking whether an IP address or email is part of a blacklist without storing the entire list in memory.
- Distributed Systems: In distributed systems like Hadoop and Cassandra, Bloom filters help in reducing disk look-ups by providing quick set membership tests before fetching data from slower storage mediums.
- Blockchain and Cryptography: Bloom filters are employed in blockchain networks, such as Bitcoin, for lightweight clients to filter transactions without downloading the entire blockchain.
\
Example - Using Bloom Filters for Geographically Separated Databases in Join Queries
Consider a scenario where multiple databases are geographically separated and need to perform a join operation on large datasets, Bloom filters can significantly reduce the amount of data transferred across the network, thus optimizing the join process.
Scenario
Imagine a company with two geographically separated databases:
- Customer Database (DB1) located in New York, containing customer information such as
CustomerID,Name, andEmail. - Order Database (DB2) located in San Francisco, containing order details such as
OrderID,CustomerID,ProductID, andOrderDate.
The goal is to perform a join operation between these two databases to generate a report of all customers and their respective orders. Performing a traditional join would require transferring the entire CustomerID list from one database to the other, which can be inefficient due to network latency and bandwidth constraints.
Bloom Filters to the Rescue
- Creating a Bloom Filter:
- First, create a Bloom filter on
DB1(Customer Database) using theCustomerIDfield. This Bloom filter will have a size and number of hash functions carefully chosen to minimize false positives while conserving space.
- Sending the Bloom Filter:
- Instead of sending the entire list of
CustomerIDvalues over the wire, the Bloom filter is sent fromDB1in New York toDB2in San Francisco. This Bloom filter is compact, requiring far less network bandwidth compared to the rawCustomerIDlist.
- Filtering Orders with the Bloom Filter:
- In
DB2(Order Database), use the received Bloom filter to check if theCustomerIDfrom the orders exists in the Bloom filter. This step quickly eliminates orders that do not match anyCustomerIDinDB1, significantly reducing the number of rows that need to be sent back toDB1. Important to note, since Bloom Filters never give us false negatives, theCustomerIDthat do not match are definitely not present inDB1. However, theCustomerIDthat do match may have false positives.
- Final Join and Report Generation:
- The filtered set of
OrderIDandCustomerIDpairs is then sent back toDB1in New York, where the final join operation is performed with the complete customer details. This approach minimizes the data transferred across the network and optimizes the overall join operation. In the final join, we can discard false positiveCustomerIDthat were detected in step 3.
Advantages of Using Bloom Filters in This Scenario
- Reduced Data Transfer: Instead of sending a potentially large list of
CustomerIDvalues, a compact Bloom filter is sent, saving bandwidth. - Efficient Filtering: Orders in
DB2that don't correspond to any customer inDB1are filtered out locally, reducing the result set size significantly. - Scalability: This approach scales well with larger datasets, where traditional methods would incur significant performance and cost penalties due to data transfer requirements.
Real-World Use Case
Bloom filters are frequently used in distributed systems for similar purposes. For example, in Google's Bigtable, Bloom filters help reduce search space, and improve read throughput when querying distributed datasets.
Advantages of Bloom Filters
- Space Efficiency: Bloom filters provide a compact representation of a set. This is particularly beneficial when dealing with large datasets or when memory is constrained.
- Speed: Checking membership in a Bloom filter is very fast, usually involving just a few hash computations and bit checks. This speed is crucial for applications requiring real-time performance.
- Scalability: Bloom filters scale well with the size of the dataset, making them suitable for large-scale applications like distributed databases and big data systems.
Limitations and Trade-offs
- False Positives: The primary drawback of Bloom filters is the possibility of false positives. An element might be reported as present even though it is not in the set. However, the false positive rate can be minimized with appropriate parameters. Bloom Filters should be used with caution, especially in cases where 100% accuracy is needed.
- No Deletions: Standard Bloom filters do not support element removal, as doing so would disturb the bit array, potentially causing false negatives. Variants like Counting Bloom Filters address this issue by using a counter instead of a single bit.
- Complexity with Union and Intersection: Operations like union and intersection are non-trivial and can lead to increased false positive rates or necessitate additional data structures.
\
Conclusion
Bloom filters offer a fascinating blend of mathematical elegance and practical utility, making them invaluable in numerous fields ranging from database management to network security. Their ability to provide fast, space-efficient membership queries comes with trade-offs that can be managed with thoughtful parameter selection and adaptations. As data volumes continue to grow, understanding and leveraging data structures like Bloom filters becomes increasingly crucial for developing efficient, scalable systems.
For anyone interested in exploring further, implementations in various programming languages are widely available, making it easy to experiment and integrate Bloom filters into real-world applications. Whether you are optimizing a database or enhancing a network filter, Bloom filters are a powerful tool to have in your arsenal.
\
References
- Fay Chang, Jeffrey Dean, Sanjay Ghemawat, Wilson C. Hsieh, Deborah A. Wallach, Mike Burrows, Tushar Chandra, Andrew Fikes, and Robert E. Gruber. 2008. Bigtable: A Distributed Storage System for Structured Data. ACM Trans. Comput. Syst. 26, 2, Article 4 (June 2008), 26 pages. https://doi.org/10.1145/1365815.1365816
- Broder, A., & Mitzenmacher, M. (2004). Network applications of Bloom filters: A survey. Internet Mathematics, 1(4), 485-509.
- https://systemdesign.one/bloom-filters-explained/
- https://cloud.google.com/blog/products/databases/cloud-bigtable-improves-single-row-read-throughput-by-up-to-50-percent/
\
This content originally appeared on HackerNoon and was authored by Vibhas Mohan Zanpure
Vibhas Mohan Zanpure | Sciencx (2024-10-16T15:00:20+00:00) Understanding Bloom Filters: An Efficient Probabilistic Data Structure. Retrieved from https://www.scien.cx/2024/10/16/understanding-bloom-filters-an-efficient-probabilistic-data-structure/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
