This content originally appeared on HackerNoon and was authored by Economic Hedging Technology
Table of Links
1.2 Asymptotic Notation (Big O)
1.5 Monte Carlo Simulation and Variance Reduction Techniques
- Literature Review
- Methodology
3.2 Theorems and Model Discussion
1.4 THE BLACK-SCHOLE MODEL
The Black-Scholes model is a cornerstone of modern financial theory, providing a mathematical framework for pricing European-style options. Developed by Fischer Black, Myron Scholes, and Robert Merton in the early 1970s, the model revolutionized the field of quantitative finance.
\ Mathematically, the Black-Scholes model calculates the price of a European call option, which gives the holder the right to buy an underlying asset at a specified price (the strike price) on or before a specified date (the expiration date). The model assumes that the price of the underlying asset follows geometric Brownian motion, characterized by a constant volatility.
\ The Black-Scholes formula for the price of a European call option is given by:
\
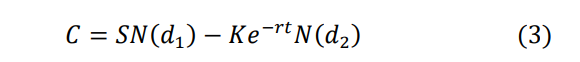
\ where
\ 𝐶 = 𝐶𝑎𝑙𝑙 𝑜𝑝𝑡𝑖𝑜𝑛 𝑝𝑟𝑖𝑐𝑒
\ 𝑆 = 𝐶𝑢𝑟𝑟𝑒𝑛𝑡 𝑝𝑟𝑖𝑐𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑢𝑛𝑑𝑒𝑟𝑙𝑦𝑖𝑛𝑔 𝑎𝑠𝑠𝑒𝑡
\ 𝐾 = 𝑆𝑡𝑟𝑖𝑘𝑒 𝑝𝑟𝑖𝑐𝑒
\ 𝑟 = 𝑅𝑖𝑠𝑘 𝑓𝑟𝑒𝑒 𝑖𝑛𝑡𝑒𝑟𝑒𝑠𝑡 𝑟𝑎𝑡𝑒
\ 𝑡 = 𝑇𝑖𝑚𝑒 𝑜𝑓 𝑒𝑥𝑝𝑖𝑟𝑎𝑡𝑖𝑜𝑛
\ 𝑁 = 𝐶𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑣𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑡ℎ𝑒 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑛𝑜𝑟𝑚𝑎𝑙 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛
\
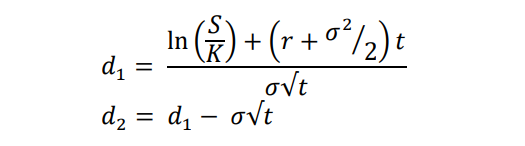
\ The formula derived from the Black-Scholes model computes the theoretical price of a call or put option based on the aforementioned factors. It considers the probability distribution of potential future asset prices and discounts expected payoffs back to the present value using the risk-free interest rate [5].
\
:::info Authors:
(1) Agni Rakshit, Department of Mathematics, National Institute of Technology, Durgapur, Durgapur, India (spiritualagnimath.statml@gmail.com);
(2) Gautam Bandyopadhyay, Department of Management Studies, National Institute of Technology, Durgapur, Durgapur, India (gbandyopadhyay.dms@nitdgp.ac.in);
(3) Tanujit Chakraborty, Department of Science and Engineering & Sorbonne Center for AI, Sorbonne University, Abu Dhabi, United Arab Emirates (tanujit.chakraborty@sorbonne.ae).
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Economic Hedging Technology
Economic Hedging Technology | Sciencx (2024-10-23T15:15:11+00:00) The Black-Scholes Model: A Fundamental Framework for Option Pricing. Retrieved from https://www.scien.cx/2024/10/23/the-black-scholes-model-a-fundamental-framework-for-option-pricing/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
