This content originally appeared on Level Up Coding - Medium and was authored by Shubh Mishra
Today, we will step away from our Vision Transformer series and discuss building a basic variant of a Generative Pre-trained Transformer (GPT).
To be more precise we will build an Auto-Regressive (bi-gram) model i.e. we will generate a token each time concerning all the previous tokens. Auto-regressive models generally sequentially generate tokens (characters or words) considering the previous tokens in the account. e.g. In the sentence “I like to eat” the next tokens for <I> <like> <to> <eat> could be <ice-cream>, <cookies>, etc.
Statistical/Classical Autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term (an imperfectly predictable term);
This imperfectly predictable or stochastic term can be very loosely [1] related to the next predicted token in our “i like to eat” example, where we help the model be less deterministic with its choice by letting it randomly choose the next token for prediction (i.e. <ice-cream>, <cookies>, etc..) which we will understand later in the article.
As we are implementing a very basic auto-regressive model we will be doing everything from scratch, using a dataset for generating Text in William Shakespeare’s style. This will be my longest article yet, so take a good breath, feel free to take breaks as needed. Let’s dive right in!”

Content
- Loading Data — Creating Data Batch Loader and Data Split.
- BigramLanguageModel — Coding the Language Model
- Training — Training the Model and Generating Text.
Note: The code in this article follows this video on GPT by none other than Andrej Karparthy. His video was in fact my very first implementation of the Attention mechanism from where I followed various other architectures and papers on Convolutional Attention, Shifted Windows, etc.
If you’ve already seen it there isn’t much difference you’ll find in the article except for minor code changes, so you can follow this one as a quick revision. If you haven’t… Let’s dive straight into it.
Loading Data
# Importing torch specific modules
import torch
import torch.nn as nn
from torch.nn import functional as F
# We start by downloading our shakespeare txt file (stored with the name input.txt)
! wget https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt */
# reading txt file (encode decode)
text = open('input.txt', 'r',).read()
vocab = sorted(list(set(text)))
encode = lambda s: [vocab.index(c) for c in s]
decode = lambda l: [vocab[c] for c in l]
Instead of using an external tokenizer, we are implementing custom lambda functions to perform character-level tokenization on our data.
ids = encode("I like to eat")
txt = decode(ids)
print(f"ids: {ids}")
print(f"txt: {txt}")
print(f"".join(txt))
# Output:-
ids: [21, 1, 50, 47, 49, 43, 1, 58, 53, 1, 43, 39, 58]
txt: ['I', ' ', 'l', 'i', 'k', 'e', ' ', 't', 'o', ' ', 'e', 'a', 't']
I like to eatSplit the data with 90/10
x = int(0.9*len(text)) # text is a big string with our entire data
text = torch.tensor(encode(text), dtype=torch.long)
train, val = text[:x], text[x:]
Remember as we are tokenizing at the character level we will be generating at the character level too, the prudent way here is to create batches of random sentences in the corpus to feed into our model for training.
batch_size = 32 # batch_size - is how many independent sequences will we process in parallel?
block_size = 8 # block_size = is the maximum context length for predictions
device = 'cuda' if torch.cuda.is_available() else 'cpu'
def get_batch(split):
# generate a small batch of data of inputs x and targets y
data = train if split == 'train' else val
ix = torch.randint(len(data) - block_size, (batch_size,))
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix])
return x.to(device), y.to(device)
xb, yb = get_batch('train')
The batch is created in the following way…
we want to get random sentences of block size (8) from the corpus so we generate indexes (ix) of batch size (32), and for each index, we take the next 8 token ids and stack for each index in the batch (ix), however our target (y) is generated with a one index more than x (i+1, i + block_size + 1) because we need to predict the next token in the sequence.
Example:-
ix = [33]
for i in ix:
print(train[i:i+18])
print(train[i+3:i+18+3]) # I've chosen +3 over +1 only for the sake of example
for i in ix:
print("".join(decode(train[i:i+18])).replace("\n", ""))
print("".join(decode(train[i+3:i+18+3])).replace("\n", ""))
# Output:-
tensor([39, 52, 63, 1, 44, 59, 56, 58, 46, 43, 56, 6, 1, 46, 43, 39, 56, 1])
tensor([ 1, 44, 59, 56, 58, 46, 43, 56, 6, 1, 46, 43, 39, 56, 1, 51, 43, 1])
any further, hear
further, hear me
BigramLanguageModel
A bi-gram is a type of n-gram where n=2, represents a sequence of two consecutive lexical units (such as words or characters) in text.
- 1-gram (Unigram) for “i like to eat”: ["i", "like", "to", "eat"]
- 2-gram (Bigram) for “i like to eat”: ["i like", "like to", "to eat"]
- 3-gram (Trigram) for “i like to eat”: ["i like to", "like to eat"]
As we are performing an Auto-regressive task we needed to load our data in the bigram format as we did in the code-block write above.
Now let’s get to the heart of the Article - The Multi-Head Attention. As I’ve already implemented this part in over a dozen articles in the Vision Transformer series, I will try to not waste your time and get straight to the concept. (Man… I would have easily stretched this blog into two parts, but screw it, let’s do it anyways)
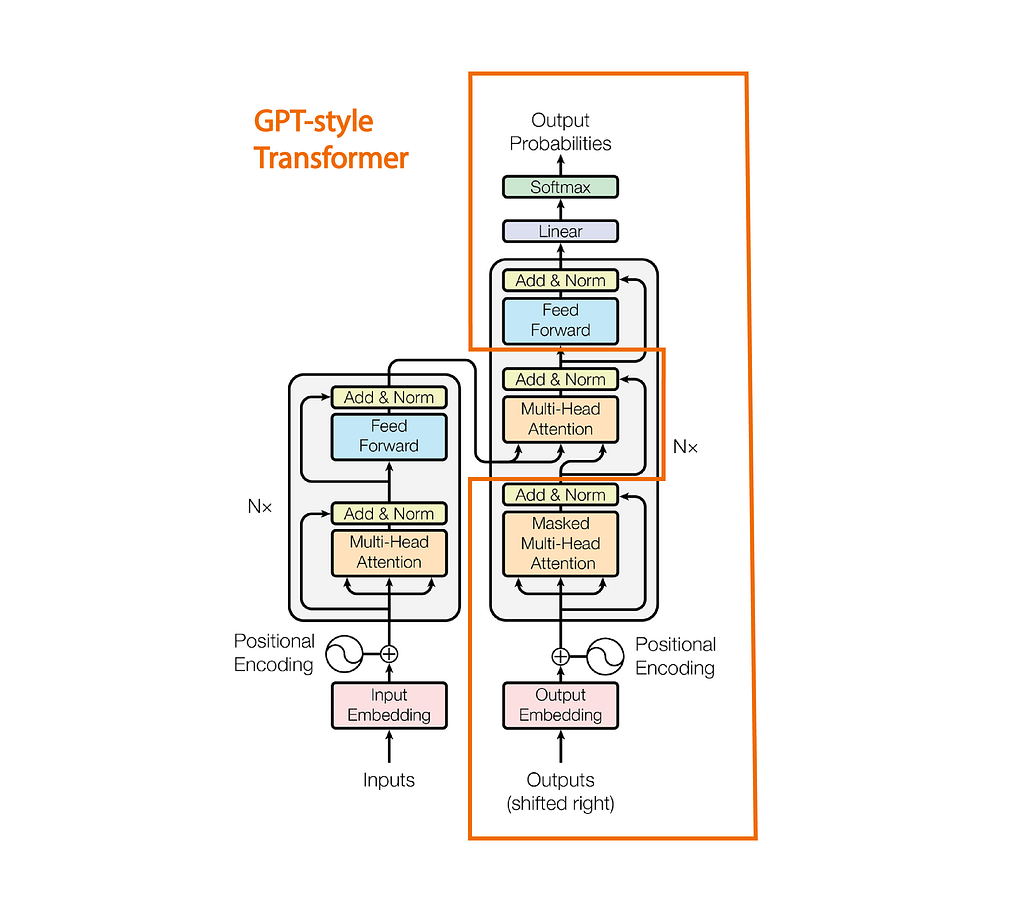
We see that GPT takes from the Transformer architecture proposed in the Attention is all you need paper. However, it differs by only stacking the Multi-Head Attention from the decoder section.
The Bigram Language Model.
class BigramLanguageModel(nn.Module):
def __init__(self, vocab_size):
super().__init__()
# each token directly reads off the logits for the next token from a lookup table
self.token_embedding_table = nn.Embedding(vocab_size, embed_size)
self.possitional_embedding = nn.Embedding(block_size, embed_size)
self.linear = nn.Linear(embed_size, vocab_size)
self.block = nn.Sequential(*[Block(embed_size, num_head) for _ in range(num_layers)])
self.layer_norm = nn.LayerNorm(embed_size)
def forward(self, idx, targets=None):
B, T = idx.shape
# idx and targets are both (B,T) tensor of integers
logits = self.token_embedding_table(idx) # (B,T,C)
ps = self.possitional_embedding(torch.arange(T, device=device))
x = logits + ps #(B, T, C)
logits = self.block(x) #(B, T, c)
logits = self.linear(self.layer_norm(logits)) # This suppose to map between embed_size and Vocab_size
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
Here the input idx is our batch that we generated earlier of shape (B, T) where T is Block Size or Token Length.
Forward pass first generates embedding for each token of shape (B, T, C) As we see in the figure above we need to add positional embedding to the token embedding. We create embeddings for the input (idx) so that we can represent the information that the token holds in a fixed embedding dimension, but this doesn’t provide any information regarding where the token is (position) that’s why we have to additionally add positional embeddings to make sure the model has context for the position of the token. If you have any doubts I would like to request that you directly refer to my prior blog where I’ve explained all of it in better detail.
nn.Embedding in PyTorch is a layer used to map discrete, categorical values (like word indices) into continuous, dense vectors. The layer takes integer indices as inputs, where each index represents a unique categorical item (e.g., a word, token, or even some other categorical data). Internally, nn.Embedding maintains an embedding matrix of shape num_embeddings, embedding_dimso it can create a dense representation of each token. As we are going for a simplistic version of GPT we are directly using nn.Embeddings to generate positional embeddings rather than going for other standard approaches.
From here, it’s straightforward... We have our Block (A stack of decoder modules) and finally, we generate new attention matrics with the same shape as the input but where each token has some information regarding all the tokens preceding it.
Finally, we apply the Layer Norm (Common practice to stabilize training) and then pass it to a linear layer to map the embedding C to our vocab dimension. The vocab dimension is simply the number of all the unique characters we have in our input.txt. One of the general ways to define how accurate our predictions are is to compare the block (attention modules) output with the target indices.
The output logits are simply supposed to be the probability distribution over vocab size V predicting the next tokens (target) in the sequence. Thus cross entropy loss is used to generate a loss for determining how close is our output with the target token sequence.
Now that we have covered the Bigram implementation. It is time to see how the Block used Multi-Head Attention (MHA) to create the attention metrics.
Multi Head Attention
The reason behind using multi-head attention is that we can directly pass the input (B, T, embedding_size) to an Attention Block but a faster approach is instead of directly generating a Q, K, V and computing attention weights of dimension embedding_size, we create sections of attention modules, calculate the attention weights separately and then concatenate them in the end.
class Head(nn.Module):
def __init__(self, head_size):
super().__init__()
self.head_size = head_size
self.key = nn.Linear(embed_size, head_size, bias=False)
self.query = nn.Linear(embed_size, head_size, bias=False)
self.value = nn.Linear(embed_size, head_size, bias=False)
def forward(self, x):
B, T, C = x.shape
k = self.key(x)
q = self.query(x)
v = self.value(x)
wei = q@k.transpose(2, 1)/self.head_size**0.5
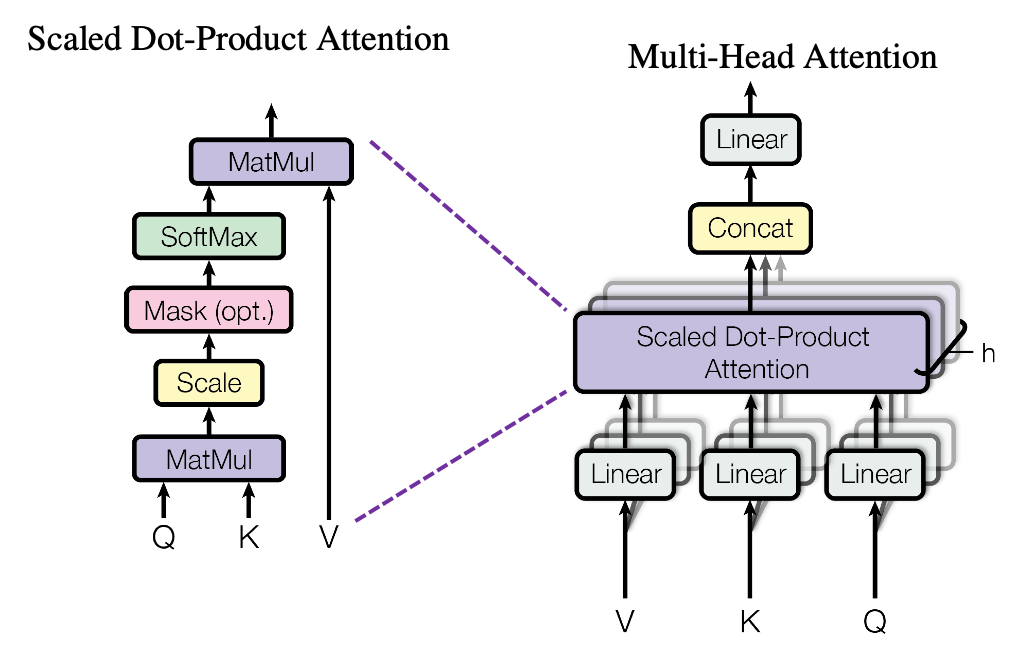
Thus following the logic above we create a single attention head. Now let’s start making some sense of it.
We have an input of dimension (batch size, token length, embed dim) after adding the positional embedding. Here, each token in the input is represented by an embed_dim (64). But no token has any information regarding all the tokens preceding it.
To create embedding enriched with such information, we use the attention mechanism, by generating Key, Query, and Value vectors.
The attention mechanism in the Head class is designed to help the model focus on different parts of the input sequence when generating the output, which is particularly useful in tasks like language modeling.
The key, query, and value projections come from the concept of querying information relevant to each token's context in the sequence. Each token is represented by a vector (x), and by linearly transforming it into separate key, query, and value vectors, we can calculate which tokens in a sequence should attend to each other.
When q (queries) is dotted with k (keys), the result (wei) tells us the "relevance" or "attention" scores between each token and every other token. Higher scores mean a token is more relevant or "important" to another token in that context. The scaling factor 1 / sqrt(head_size) prevents these scores from getting too large, which can make the softmax distribution too sharp and harder to optimize.
class Head(nn.Module):
def __init__(self, head_size):
super().__init__()
self.head_size = head_size
self.key = nn.Linear(embed_size, head_size, bias=False)
self.query = nn.Linear(embed_size, head_size, bias=False)
self.value = nn.Linear(embed_size, head_size, bias=False)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
self.dropout = nn.Dropout(dropout)
def forward(self, x):
B, T, C = x.shape
k = self.key(x)
q = self.query(x)
v = self.value(x)
wei = q@k.transpose(2, 1)/self.head_size**0.5
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf'))
wei = F.softmax(wei, dim=2) # (B , block_size, block_size)
wei = self.dropout(wei)
out = wei@v
return out
The causal mask, tril, is applied to ensure that each token can only "see" itself and previous tokens. This is crucial for autoregressive tasks like text generation, where the model should not look ahead at future tokens when predicting the next one. Setting irrelevant positions to negative infinity masked_fill makes them zero after softmax, so they don't contribute to the final attention calculation. This keeps the model from cheating by looking at future tokens as we want to predict the future token. Finally, we take a dot product between the weight and value metrics and return our output.
You can check this example output to get a better sense of the transformations that happen:
q = torch.randint(10, (1, 3, 3))
v = torch.randint(10, (1, 3, 3))
print("Query:\n",q)
print("Value:\n",v)
wei = q@v.transpose(2, 1)/3**0.5
print("weights:\n", wei)
tril = torch.tril(torch.ones(3, 3))
print("Triangular Metrics:\n",tril)
wei = wei.masked_fill(tril == 0, float('-inf'))
print("Masked Weights\n", wei)
print("Softmax ( e^-inf = 0 )\n", F.softmax(wei, dim=2))
# Output:-
Query:
tensor([[[2, 8, 8],
[4, 2, 4],
[1, 2, 9]]])
Value:
tensor([[[9, 5, 7],
[3, 1, 4],
[6, 2, 9]]])
weights:
tensor([[[65.8179, 26.5581, 57.7350],
[42.7239, 17.3205, 36.9504],
[47.3427, 23.6714, 52.5389]]])
Triangular Metrics:
tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 1., 1.]])
Masked Weights
tensor([[[65.8179, -inf, -inf],
[42.7239, 17.3205, -inf],
[47.3427, 23.6714, 52.5389]]])
Softmax ( e^-inf = 0 )
tensor([[[1.0000e+00, 0.0000e+00, 0.0000e+00],
[1.0000e+00, 9.2777e-12, 0.0000e+00],
[5.5073e-03, 2.8880e-13, 9.9449e-01]]])
As we are using multi-head attention this is how we will implement it:
class MultiHeadAttention(nn.Module):
def __init__(self, head_size, num_head):
super().__init__()
self.sa_head = nn.ModuleList([Head(head_size) for _ in range(num_head)])
self.dropout = nn.Dropout(dropout)
self.proj = nn.Linear(embed_size, embed_size)
def forward(self, x):
x = torch.cat([head(x) for head in self.sa_head], dim= -1)
x = self.dropout(self.proj(x))
return x
Here we are passing the input x (B, T, E) to different attention heads, where each attention head returns the final vector of size (B, T, head_size) where head size = E (64) / num heads (4) = 16, as we do it in a for loop of range(num_head(4)) we concatenate it back to it’s original size (B, T, 4*16).
Multihead attention is simply considered faster and much more efficient at the scale where the embedding dimension is even greater.
After concatenation we pass the final output to the linear projection layer, the sense of this is to enable the embeddings in the final vector to further communicate what they have learned about each other during the attention weight computation. After which it is passed to a dropout layer and returned.
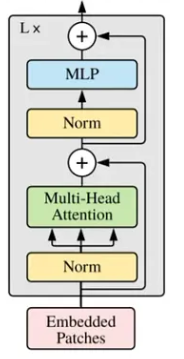
Putting it all together, the standard decoder block is implemented as shown in Figure 1 above.
class FeedForward(nn.Module):
def __init__(self, embed_size):
super().__init__()
self.ff = nn.Sequential(
nn.Linear(embed_size, 4*embed_size),
nn.ReLU(),
nn.Linear(4*embed_size, embed_size),
nn.Dropout(dropout)
)
def forward(self, x):
return self.ff(x)
class Block(nn.Module):
def __init__(self, embed_size, num_head):
super().__init__()
head_size = embed_size // num_head
self.multihead = MultiHeadAttention(head_size, num_head)
self.ff = FeedForward(embed_size)
self.ll1 = nn.LayerNorm(embed_size)
self.ll2 = nn.LayerNorm(embed_size)
def forward(self, x):
x = x + self.multihead(self.ll1(x))
x = x + self.ff(self.ll2(x))
return x
The head size is calculated as explained earlier, the input is simply passed through a layer norm followed by our multi-head attention network and then another layer norm finally passing through a feed-forward network.
Getting Back to the Bigram Model
class BigramLanguageModel(nn.Module):
def __init__(self, vocab_size):
super().__init__()
# each token directly reads off the logits for the next token from a lookup table
self.token_embedding_table = nn.Embedding(vocab_size, embed_size)
self.possitional_embedding = nn.Embedding(block_size, embed_size)
self.linear = nn.Linear(embed_size, vocab_size)
self.block = nn.Sequential(*[Block(embed_size, num_head) for _ in range(num_layers)])
self.layer_norm = nn.LayerNorm(embed_size)
def forward(self, idx, targets=None):
B, T = idx.shape
# idx and targets are both (B,T) tensor of integers
logits = self.token_embedding_table(idx) # (B,T,C)
ps = self.possitional_embedding(torch.arange(T, device=device))
x = logits + ps #(B, T, C)
logits = self.block(x) #(B, T, c)
logits = self.linear(self.layer_norm(logits)) # This suppose to map between head_size and Vocab_size
if targets is None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# crop idx to the last block_size tokens
crop_idx= idx[:, -block_size:].to(device)
# get the predictions
logits, loss = self(crop_idx)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C) from (B, T, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# We sample one index from the filtered distribution
idx_next = torch.multinomial(probs, num_samples=1).to(device)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
Here we see that the Block is called under the Sequential layer through the range of the number of layers.
Generating tokens…
We start by passing the single dimension idx tensor (indices for our tokens) to the generate function along with the maximum number of new tokens we want to generate. As our model is built for block size 8, we can only pass 8 tokens at a time, thus we crop the last 8 tokens in the idx (all tokens are selected if idx length is less than the block size).
We pass the crop idx to our BigramLanguageModel, as the logits we generated had the probable distribution of the target tokens, we are only interested in the last token as the last token of the targets (y) is the next in the sequence (x) (explained in batch loader section).
The logits we have now, are of shape (B, C) where C is the Vocab Size, which represents the probability distribution over the entire vocab for the last token index. Now we simply apply a softmax over it to turn this vector into a probability vector (i.e. sum of elements = 1).
Now, remember how we at the very beginning of the article talked about imperfectly predictable or stochastic terms and how we let the model randomly select what is going to be the next token in the sequence? To do so we use torch.multinomial which is a statistical strategy used to take out a sample from a given probability distribution. Here it samples the indices randomly according to the specified probabilities.
We then finally get the next idx predicted, concatenate it with the previous idx, and then continue the for loop to keep generating the next index based on the previous ones till we reach the max tokens.
Training
Luckily the training part is very straightforward.
m = BigramLanguageModel(65).to(device)
optimizer = torch.optim.AdamW(m.parameters(), lr=1e-3)
# training the model, cause I won't give up without a fight
batch_size = 32
for epoch in range(5000):
# Printing the Training and Validation Loss
if epoch%1000==0:
m.eval()
Loss= 0.0
Val_Loss = 0.0
for k in range(200):
x, y = get_batch(True)
val_ , val_loss = m(x, y)
x1, y1 = get_batch(False)
_, train_loss = m(x1, y1)
Loss += train_loss.item()
Val_Loss += val_loss.item()
avg_loss = Val_Loss/(k+1)
avg_train_loss = Loss/(k+1)
m.train()
print("Epoch: {} \n The validation loss is:{} The Loss is:{}".format(epoch, avg_loss, avg_train_loss))
# Forward
data, target = get_batch(False)
logits, loss = m(data, target)
#Backward
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
Here we keep the train for 5000 epochs, which relatively takes roughly about 2 minutes in 4 GB VRAM Nvidia RTX 3050.
We start with the Forward Pass by fetching our batch from get_batch() and passing it to our BigramLanguageModel. Setting optimizer.zero_grad(), doing loss. backward(), and performing an optimizer.step(), we utilize an AdamW Optimizer which is far more enough for what we need it for.
Now the moment you were waiting for..
We create a tensor for the following sentence:
ids = torch.tensor(encode("i like to eat food"), dtype=torch.long).unsqueeze(0)The shape of ids is with shape (1, 18) (Batch Size, Token). Starting with just 18 tokens (representing indices in our vocabulary) and generating 2000 more characters. For context, our vocab is the set of all unique characters in the input.txt which we implemented earlier under the Data Loading Section i.e. vocab = sorted(list(set(text)))
print("".join(decode(m.generate(torch.zeros([1,1], dtype=torch.long) , max_new_tokens=2000)[0].tolist())))Output:-
i like to eat food, noBANIO:
Here and
I shake married entreature by colantied at to women oword this swamind-betweet you are
As Grave eare his sun.
LUCENTIO:
Go what a doubled mistressed well.
Taildoes, not to memble, the peashat you;--are master, in thou comsand of the for slawake to bound and to of off this couchio;
Petruchio?
Fece poor this cockepopen neve so it do old loaps islied I'comment and curh
and blate sure poccient you the miad e'er a to partink,
Unory speitied where buzzarr'd formorns,
Pitedame,
Beach, and whom I firit.
ANDO:
O the virtuus a parros that that is acleast, not for suck could mighreature well; thy,
I'll toence after counteent,
Signior to paptista?
Shile you cappier?
BIANCA:
Where womand betire asleck him snall conglithing.
PROSPERO:
I, as expase caspierfed success,
This all no be trutes from the good the island mognied buzent; tensting in this garmortwant;
Do be marriage.
TRANIO:
'Tis, jointer.
GRUCHIO:
Soubt sI'll show I freek born.
PROSPETRUCHIO:
The vant mine; it it

I know… It doesn’t make sense. But we must realize that Language Models are not trained on mere datasets of Shakespeare's writings. It takes a vast amount of GPU power, with better tokenization techniques and really large corpus of datasets.
As we trained it on a very small model, our performance is not bad, the output still makes sense, and have learned to use actual English words than to generate random gibberish.
You can try to experiment with the model, for different datasets and Token Size, Batch Size, Number of Layers, etc.
Thank You!
The main goal of this blog was to explain to you in detail how you can build your language model from scratch and train it on your dataset,... Well, now you know!!!
With this, I can’t thank you enough for giving learning a chance and reading it so far, I hope that you enjoyed reading this one. The entire code is available here on my GitHub repository ML-Models where I implement various deep learning architectures from scratch.
If you liked this article or found it informative please consider giving it a clap and dropping me a follow. If you have any doubts feel free to reach out.
Thanks for reading!
References:
[1] Large language models are called autoregressive, but they are not a classical autoregressive model in this sense because they are not linear. Read More.
Let’s Build our own GPT Model from Scratch with PyTorch was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Shubh Mishra
Shubh Mishra | Sciencx (2024-11-08T01:32:41+00:00) Let’s Build our own GPT Model from Scratch with PyTorch. Retrieved from https://www.scien.cx/2024/11/08/lets-build-our-own-gpt-model-from-scratch-with-pytorch/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
