This content originally appeared on Level Up Coding - Medium and was authored by Sanjay Nandakumar
Understanding the Limitations; Why Bigger Isn’t Always Better for Critical Applications
Table of Contents
- Introduction
2. Problem 1: Overfitting and Lack of Generalization
- Mathematical Explanation of Overfitting (with Jupyter Notebook Illustration)
- Real-Life Example: Misdiagnosis in Healthcare
- Python Code: Bias-Variance Illustration
3. Problem 2: Limited Contextual Understanding and Memory Constraints
- Mathematical Explanation of Self-Attention (with Jupyter Notebook Illustration)
- Real-World Example: Financial Analysis and Long-Term Dependencies
- Python Code: Demonstrating Contextual Limitations
4. Problem 3: Probabilistic Nature vs. Deterministic Requirements
- Mathematical Explanation of Probabilistic Predictions (with Jupyter Notebook Illustration)
- Illustrative Example: Legal Analysis and Sentencing
- Python Code: Probabilistic Recommendations
5. Problem 4: Lack of Causal Understanding
- Mathematical Explanation of Causality (with Jupyter Notebook Illustration)
- Hypothetical Example: Healthcare Policy Analysis
- Python Code: Correlation-Based Approach
6. Problem 5: Handling Out-of-Distribution (OOD) Data
- Mathematical Explanation of OOD Data (with Jupyter Notebook Illustration)
- Real-Life Example: Cybersecurity Breaches
- Python Code: Handling OOD Data with Isolation Forest
7. The Way Forward: Potential Solutions to Overcome LLM Limitations
- Hybrid Models for Causal Reasoning
- Memory-Enhanced Architectures
- Reinforcement Learning for Critical Decision-Making
- Explainability Frameworks for Critical Applications
8. Conclusion
Introduction
Sophisticated NLPs known as advanced LLMs like GPT-4, Claude, etc., have helped revolutionize the field of Natural Language Processing (NLP). These display impressive fluency and comprehension, boasting billions of parameters and trained on terabytes of data. Advanced though they may be, LLMs often need help to control mission-critical use cases, such as medical diagnosis, legal decision-making, or high-stakes financial forecasting.
This article will explore the underlying reasons for these failures, grounded in machine learning, probability theory, and statistics. Moreover, we will study real examples, include relevant Python code snippets, and, if feasible, propose some possible solutions.
Problem 1: Overfitting and Lack of Generalization
Theoretical Background: Bias-Variance Tradeoff
In machine learning, the bias-variance tradeoff is a well-known fundamental principle that explains the generalization capabilities of our model. LLMs are typically trained on huge datasets and will learn patterns from these data, which might lead to overfitting if the model adapts and learns these patterns until fitting noise or other uncertainties in the given example.
Mathematical Explanation:
Given a model f(x), the expected error can be expressed as:
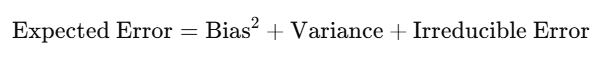
Bias refers to the error introduced from oversimplification, while variance refers to a model’s sensibility of small fluctuations in the training set. LLMs are usually optimized to minimize bias, thus leading to high variance and overfitting.
Real-Life Example: Misdiagnosis in Healthcare
When misdiagnosing rare diseases, healthcare requires models to generalize more than just common patterns. Overfitting such a model for common ailments would thereby render it ineffective against rare disorders, leading to misdiagnosis. In cases where symptoms indicative of a life-threatening condition are rare, misdiagnosis could be fatal.
Python Simulation: Bias-Variance Illustration
# Import necessary libraries
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
# Simulate data
# Set a random seed for reproducibility
np.random.seed(42)
# Generate 100 random values for X between -1 and 1
X = np.random.rand(100, 1) * 2 - 1
# Define the relationship between X and y with some noise
# The relationship is a quadratic function plus some random noise
y = 4 * (X ** 2) + np.random.randn(100, 1) * 0.1
# Fit a polynomial model with a high degree (overfitting scenario)
# Create polynomial features up to degree 15
poly = PolynomialFeatures(degree=15)
# Transform X into polynomial features
X_poly = poly.fit_transform(X)
# Fit a linear regression model on the polynomial features
model = LinearRegression()
model.fit(X_poly, y)
# Predict on new, unseen data points
# Create a range of new X values from -1 to 1 for prediction
X_new = np.linspace(-1, 1, 100).reshape(-1, 1)
# Transform the new X values into polynomial features using the same degree
X_new_poly = poly.transform(X_new)
# Use the model to make predictions on the new polynomial-transformed data
y_pred = model.predict(X_new_poly)
# Plotting the overfitted model to visualize the results
import matplotlib.pyplot as plt
plt.scatter(X, y, color="blue", label="Original Data") # Scatter plot of original data points
plt.plot(X_new, y_pred, color="red", label="Model Prediction") # Plot of the model's prediction
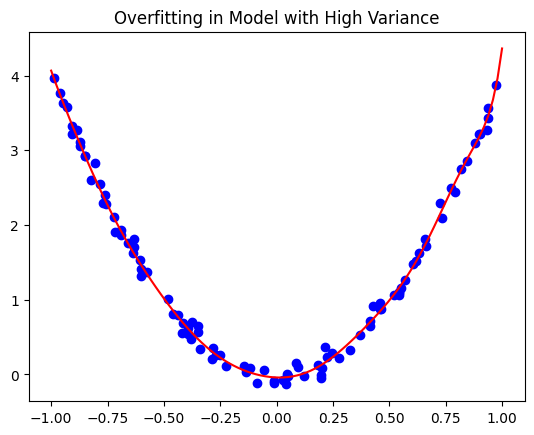
plt.title("Overfitting in Model with High Variance") # Title of the plot
plt.legend() # Add a legend to distinguish between original data and prediction
plt.show() # Display the plot
Problem 2: Limited Contextual Understanding and Memory Constraints
Theoretical Background: Self-Attention and Transformer Models
The Transformer architecture introduced the concept of self-attention, which allows LLMs to process the tokens in parallel and depend on one another. The experiments show that even though it does well in all tasks, it has an inherent limitation of being unable to handle long-term dependencies or relationships across documents due to its finite token window.
Mathematical Explanation:
The self-attention mechanism operates on a set of input tokens X={x1,x2,…,xn} and calculates attention scores based on:
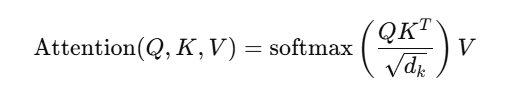
Q, K, and V are labels for the query, key, and value matrices with 𝑑𝑘 as the scaling value. But as more and more input tokens come in, the better an ML model becomes at linking those distant tokens-a process that enables the process to act somewhat independently at a semantic level and keep coherence intact.
Real-World Example: Financial analysis
Financial analysts use historical data over decades to predict market trends. A model trained with limited context windows may not link key events between a past recession and the current economic situation.
Python Simulation: Context Limitation
# Import the necessary classes from the transformers library
from transformers import GPT2Tokenizer, GPT2LMHeadModel
# Load the pre-trained GPT-2 tokenizer
# The tokenizer is responsible for converting text into token IDs that the model understands
tokenizer = GPT2Tokenizer.from_pretrained("gpt2")
# Load the pre-trained GPT-2 model with a language modeling head
# This model can generate text based on the input tokens
model = GPT2LMHeadModel.from_pretrained("gpt2")
# Define the input text that we want to generate additional text for
input_text = "In the 2008 financial crisis, market downturns created a massive loss of wealth. In 2023, the implications of the COVID-19 pandemic on global markets..."
# Encode the input text into token IDs that the model can process
# 'return_tensors' specifies that we want the output in PyTorch tensor format
input_ids = tokenizer.encode(input_text, return_tensors='pt')
# Generate text with the model based on the input IDs
# 'max_length' specifies the total length of the generated sequence (including the input text)
# 'do_sample=False' means we want to use greedy decoding, which selects the most probable word at each step
output = model.generate(input_ids, max_length=50, do_sample=False)
# Decode the output token IDs back into human-readable text, skipping special tokens
decoded_output = tokenizer.decode(output[0], skip_special_tokens=True)
# Print the generated text
print(decoded_output)
Problem 3: that poses itself is a problem of a probabilistic nature which is opposed to the deterministic requirement.
Theoretical Background: Probability Distributions and Bayesian Inference
Unlike the probabilistic models adopted by LLMs in predicting the likelihood of various outcomes based on training data, there are certain applications where truly deterministic answers are called for, for example, in healthcare and legal settings, where decisions can literally have life-altering implications.
Mathematical Explanation:
LLMs rely on maximum likelihood estimation (MLE), predicting the most likely outcome y∗ for a given input xxx as:
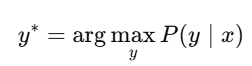
In contrast, deterministic systems often require minimizing uncertainty through specific algorithms like Bayesian inference:
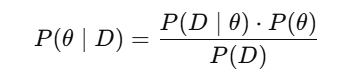
where θ represents model parameters and D is the data.
An Illustrative Example: Legal Analysis and Sentencing
In law, one must determine a sentence that is beyond a reasonable doubt. Some statistical models, in making a sentencing decision based on standard probabilities, risk producing orders that do not conform to justice.
Python Simulation: Probabilistic Recommendations
import numpy as np
# Define the probabilities of different case outcomes based on precedents
# Each key in the dictionary represents a potential case outcome, and the corresponding value is the probability of that outcome
case_prob = {
"Plea Bargain": 0.4, # Probability of a plea bargain
"Guilty Verdict": 0.5, # Probability of a guilty verdict
"Mistrial": 0.1 # Probability of a mistrial
}
# Determine the outcome with the highest probability
# 'max' function is used to find the key with the maximum value (probability) in the dictionary
recommended_verdict = max(case_prob, key=case_prob.get)
# Print the recommended outcome based on the highest probability
print(f"Recommended outcome based on probability: {recommended_verdict}")

Problem 4: Lack of Causal Understanding
Theoretical Background: Correlation vs. Causation
LLMs are ultimately correlation-based models. Their learning is pattern-detecting without being informed about what caused that pattern. On the other hand, critical use cases need to establish causality in order to accurately infer outcomes.
Mathematical Explanation:
Shifting the focus of observation from the current known world to a different hypothetical one is often done through counterfactual reasoning, and we always compare the actual outcomes to what could have happened. Here, this can be expressed mathematically by potential outcomes:
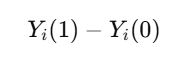
Y represents the outcome if treatment is given, and Y whenever treatment is not available.
Hypothetical Example: Healthcare Policy Analysis
In healthcare policy analysis, the effects of a new intervention should be looked upon causally, rather than just in terms of correlation. LLMs might be able to state the correlation between the implementation of certain policies and affected outcomes but are not effective in directing a causal path.
Python Simulation: Correlation-Based Approach
import pandas as pd
from sklearn.linear_model import LinearRegression
# Create a simulated dataset with correlated variables (Ad Spend and Sales)
data = pd.DataFrame({
"Ad_Spend": [100, 200, 300, 400, 500], # Advertising spend in some currency unit
"Sales": [20, 40, 50, 70, 80] # Corresponding sales resulting from the Ad spend
})
# Define the feature (X) and target variable (y) for the model
X = data[["Ad_Spend"]] # Independent variable (Advertising spend)
y = data["Sales"] # Dependent variable (Sales)
# Train a simple linear regression model on the dataset
model = LinearRegression()
model.fit(X, y) # Fit the model with the feature X and target y
# Predict the sales value based on a new Ad_Spend value of 600
predicted_sales = model.predict([[600]])
# Print the predicted sales value
print(f"Predicted Sales with 600 Ad Spend: {predicted_sales[0]}")

Problem 5: Handling Out-of-Distribution (OOD) Data
Theoretical Background: OOD Detection and Transfer Learning
LLMs are normally trained on numerous datasets; however, when trained on such datasets, LLMs still cannot recognize (OOS) out-of-distribution data. In actual situations, novel events or edge cases call for more flexibility than usually offered by LLMs.
Mathematical Explanation:
Models such as Isolation Forests determine anomalous data in a dataset through their decision paths in a random forest framework. However, LLMs do not explicitly contain any anomaly detection approaches and hence tend to perform very poorly when it comes to OOD detection.
Real-Life Example-Cybersecurity Breaches
There is an ever-increasing number of threat vectors in cybersecurity. An LLM that has been trained only on known patterns of an attack may entirely fail to identify any new age zero-day exploit attacks, thus subjecting all systems to breach.
Python Simulation: OOD Handling
from sklearn.ensemble import IsolationForest
import numpy as np
# Simulate in-distribution data using a normal distribution centered at 0 with a standard deviation of 1
in_distribution_data = np.random.normal(loc=0.0, scale=1.0, size=(100, 2))
# Create out-of-distribution (OOD) data points that are clearly outside the distribution of in-distribution data
out_of_distribution_data = np.array([[5, 5], [6, 6]])
# Initialize the Isolation Forest model
# The 'contamination' parameter defines the proportion of outliers expected in the dataset (10% in this case)
model = IsolationForest(contamination=0.1)
# Fit the Isolation Forest model using only the in-distribution data
model.fit(in_distribution_data)
# Predict the labels for the out-of-distribution data
# The model will predict -1 for outliers (OOD data) and 1 for inliers (in-distribution data)
out_of_distribution_predictions = model.predict(out_of_distribution_data)
# Print the predictions for the OOD data
print("OOD Predictions:", out_of_distribution_predictions) # Output: -1 indicates OOD data detected

Here, it is a demonstration that how an anomaly detection algorithm, Isolation Forest, can identify out-of-distribution data. While large language models do not have defined means to identify out-of-distribution data, this could be one of the drawbacks.
The Way Forward: Potential Solutions to Overcome LLM Limitations
1. Hybrid Models for Causal Reasoning
A viable solution which could fill the existing gap between correlation-based learning and causal understanding would be to integrate the LLMs with the causal models, such as SCMs. This way, the LLMs get to apply their pattern space capabilities while the causal model imposes a structurality on how we understand relationships that go beyond correlation alone.
For example, in healthcare, a hybrid model in which an LLM works together with SCM might put forth a diagnosis not purely based on the patient’s symptoms but also coming into play alongside the knowledge of the known causal factors such as patient history, environmental exposures, and genetic predispositions.
2. Memory-Enhanced Architectures
LLMs like GPT-4 encounter difficulties in maintaining long-term dependencies mainly because of the token limit. DNCs and transformers with Memory Networks accomplish this by linking external memory, which lets the model store and recall information over longer periods.
Technical Insight: The DNC itself uses read-write mechanisms for storing information, which allows the system to hold onto information across learning tasks, greatly increasing coherence with extended contexts.
Python Simulation: Memory-Augmented Transformer
import torch
import torch.nn as nn
# Pseudo-code: Memory-Augmented Transformer (MAT) Implementation
class MemoryAugmentedTransformer(nn.Module):
def __init__(self, num_memory_slots, memory_size):
super(MemoryAugmentedTransformer, self).__init__()
# Initialize memory slots as learnable parameters
# Memory slots are randomly initialized and will be learned during training
self.memory_slots = nn.Parameter(torch.randn(num_memory_slots, memory_size))
# Define a transformer encoder layer with specified memory size and number of attention heads
# d_model specifies the size of each input sample's embedding, and nhead specifies the number of heads in multi-head attention
encoder_layer = nn.TransformerEncoderLayer(d_model=memory_size, nhead=2)
# Define a transformer encoder using a single layer (num_layers = 1)
self.transformer_layer = nn.TransformerEncoder(encoder_layer, num_layers=1)
def forward(self, input_seq):
# Get the batch size from the input sequence
batch_size = input_seq.size(0)
# Expand memory slots to match the batch size, creating a batch of memory slots for each input in the batch
expanded_memory = self.memory_slots.unsqueeze(0).expand(batch_size, -1, -1)
# Concatenate the input sequence with the expanded memory slots along the sequence length dimension (dim=1)
combined_input = torch.cat((input_seq, expanded_memory), dim=1)
# Pass the combined input through the transformer encoder layer
memory_attention = self.transformer_layer(combined_input)
# Extract the output corresponding to the original input sequence (ignoring the additional memory slots)
# Add the residual connection by summing the original input sequence and its corresponding portion from the output
output = memory_attention[:, :input_seq.size(1), :] + input_seq
# Return the final output
return output
# Define model parameters: number of memory slots and the size of each memory slot
num_memory_slots = 5
memory_size = 16
# Instantiate the Memory-Augmented Transformer model with the defined parameters
model = MemoryAugmentedTransformer(num_memory_slots, memory_size)
# Create a dummy input tensor with a batch size of 2, sequence length of 10, and dimension size of 16
dummy_input = torch.randn(2, 10, memory_size)
# Forward pass through the model with the dummy input
output = model(dummy_input)
# Print the shape of the output tensor
print("Output shape:", output.shape)
# Print the output tensor itself
print("Output tensor:", output)

The above pseudo-code shows how memory slots can be incorporated into transformer architecture. This is required for any contextual extension of the architecture — including several paragraphs in machine translation or whole videos in video captioning.
3. Reinforcement Learning for Critical Decision-Making
RL is available for incorporation with LLMs if deterministic decision-making is important in a given application. In particular, in this realm of applications, RL allows the automated identification and estimation of several situations followed by learning-optimizing action-policy selections according to a predefined reward function.
Example: An LLM-RL hybrid generates insights about what to market in financial forecasting, simulating various investment strategies, and continuously improving its predictions based on some form of live feedback.
Python Simulation: Simple RL Integration
import numpy as np
# Define a simple Q-learning agent class
class SimpleQLearningAgent:
def __init__(self, alpha=0.1, gamma=0.9, epsilon=0.1):
# Initialize the Q-table as an empty dictionary
self.q_table = {}
# Learning rate (how quickly the agent updates its Q-values)
self.alpha = alpha
# Discount factor (how much the agent values future rewards)
self.gamma = gamma
# Epsilon (probability of choosing a random action for exploration)
self.epsilon = epsilon
def get_action(self, state, actions):
# Choose an action based on an epsilon-greedy strategy
if np.random.rand() < self.epsilon:
# With probability epsilon, choose a random action (explore)
return np.random.choice(actions)
else:
# Otherwise, choose the action with the highest Q-value (exploit)
return max(actions, key=lambda a: self.q_table.get((state, a), 0))
def update_q_value(self, state, action, reward, next_state, next_actions):
# Get the current Q-value for the given state-action pair
old_value = self.q_table.get((state, action), 0)
# Estimate the maximum future reward from the next state
future_reward = max([self.q_table.get((next_state, a), 0) for a in next_actions], default=0)
# Update the Q-value using the Q-learning formula
self.q_table[(state, action)] = old_value + self.alpha * (reward + self.gamma * future_reward - old_value)
# Initialize the agent with specified hyperparameters
agent = SimpleQLearningAgent(alpha=0.1, gamma=0.9, epsilon=0.1)
# Define the environment with states and actions
states = ["A", "B", "C"]
actions = ["Left", "Right"]
# Define the reward function as a dictionary mapping (state, action) pairs to (next state, reward)
rewards = {
("A", "Right"): ("B", 10),
("B", "Left"): ("A", 5),
("B", "Right"): ("C", 20),
("C", "Left"): ("B", 15)
}
# Simulate a learning process over multiple episodes
for episode in range(100): # Simulate 100 episodes of learning
current_state = "A" # Start each episode from state "A"
while current_state != "C": # Keep going until we reach the terminal state "C"
# Choose an action based on the current state using the agent's policy
action = agent.get_action(current_state, actions)
# Determine the next state and reward based on the chosen action
if (current_state, action) in rewards:
next_state, reward = rewards[(current_state, action)]
else:
next_state, reward = current_state, 0 # No change in state if the action is invalid
# Update the Q-value for the chosen action using the agent's learning method
agent.update_q_value(current_state, action, reward, next_state, actions)
# Move to the next state
current_state = next_state
# Print the learned Q-table after training
for state_action, value in agent.q_table.items():
print(f"State-Action: {state_action}, Q-Value: {value:.2f}")

Using Q-learning, this primitive RL agent optimizes actions according to the reward function, signifying how reinforcement learning could direct actions based on insights generated by an LLM.
4. Explainability Frameworks for Critical Applications
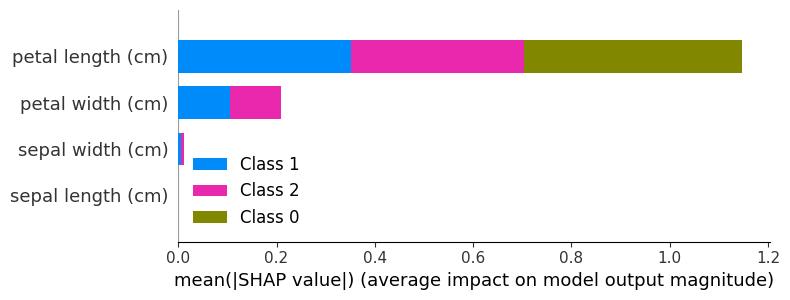
In critical applications, trust and accountability are quite important. Explainable AI (XAI) techniques such as SHAP (Shapley Additive Explanations), LIME (Local Interpretable Model-agnostic Explanations), and attention visualization offer great insight into the model decision-making process and deliver transparency and accountability in decision-making.
Example: In healthcare, employing SHAP values to explain why an LLM recommended a particular treatment can allow clinicians to develop trust in AI-driven decisions.
Python Simulation: Explainability with SHAP
# Import necessary libraries
import shap
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import numpy as np
# Load the Iris dataset from sklearn
iris = load_iris()
# Separate the data (X) and target (y) into a pandas DataFrame
X, y = pd.DataFrame(iris.data, columns=iris.feature_names), iris.target
# Train a Decision Tree Classifier
# Split the dataset into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Instantiate and fit the Decision Tree model
model = DecisionTreeClassifier(random_state=42)
model.fit(X_train, y_train)
# Create a SHAP explainer object for the trained decision tree model
explainer = shap.TreeExplainer(model)
# Calculate SHAP values for the test set
# SHAP values measure the contribution of each feature to the model's predictions
shap_values = explainer.shap_values(X_test)
# Check if the shap_values are in a 3D array format (multi-class problem)
# For multi-class classification problems, shap_values will be a 3D array,
# so we need to convert it to a list of 2D arrays for compatibility with shap.summary_plot
if isinstance(shap_values, np.ndarray) and shap_values.ndim == 3:
shap_values = [shap_values[:, :, i] for i in range(shap_values.shape[2])]
# Display a summary plot of SHAP values
# plot_type="bar" provides a bar plot of mean absolute SHAP values for each feature
# Convert iris.feature_names to a simple Python list for display in the plot
shap.summary_plot(shap_values, X_test, plot_type="bar", feature_names=list(iris.feature_names))
Conclusion
While models such as GPT-4 and Claude have made notable leaps forward, essential problems remain with respect to their applicability in these very applications. Such problems include overfitting, limited contextual comprehension, probabilistic reasoning and not deterministic reasoning, non-causal understanding, and scarcity in handling out-of-distribution data.
To overcome the above challenges, a multi-pronged approach must be taken:
- Overfitting and Generalization: Focus on building architectures that handle the bias-variance tradeoffs appropriately.
- Context and Memory Limitations: Develop memory-augmented architectures to hold pertinent information over long sequences.
- Deterministic Requirements: Merge reinforcement learning with LLMs for deterministic decision-making within high-stake scenarios.
- Causal Reasoning: Develop hybrid models combining LLM capabilities with causal inference techniques.
- OOD Data Handling: Start integrating anomaly detection mechanisms with transfer learning to handle new scenarios.
The management of limitations in strategic ways would allow LLMs to evolve so that not only do they undertake text-based tasks, but they operate reliably and explainably in critical real-life applications.
Thus, programming examples were uploaded to my GitHub repository, and you can try out codes according to your requirements - URL
Note: The aim of this article is to trigger thinking and insight into the limitations of LLMs in critical applications. The examples and code contained are for illustrative purposes and should not be deployed within high-stake settings without appropriate vetting and supervision from domain experts.
Why Advanced LLMs, Such as GPT-4 or Claude, Fail in Critical Use Cases Despite Large Training Data was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Sanjay Nandakumar
Sanjay Nandakumar | Sciencx (2024-11-08T01:32:38+00:00) Why Advanced LLMs, Such as GPT-4 or Claude, Fail in Critical Use Cases Despite Large Training Data. Retrieved from https://www.scien.cx/2024/11/08/why-advanced-llms-such-as-gpt-4-or-claude-fail-in-critical-use-cases-despite-large-training-data/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
