This content originally appeared on Level Up Coding - Medium and was authored by Sarvesh Khetan
Transformer Architecture
Table of Contents :
- Single Head Self Attention Transformer
1.a. Vector Implementation
1.b. Matrix Implementation
1.c. Positional Encodings
1.c.1. Absolution Positional Encodings
1.c.2. Relative Positional Encodings — Rotary Positional Encodings (RoPE) - Multi Head Self Attention Transformer
2.a Matrix Implementation

Single Head Self Attention Transformer
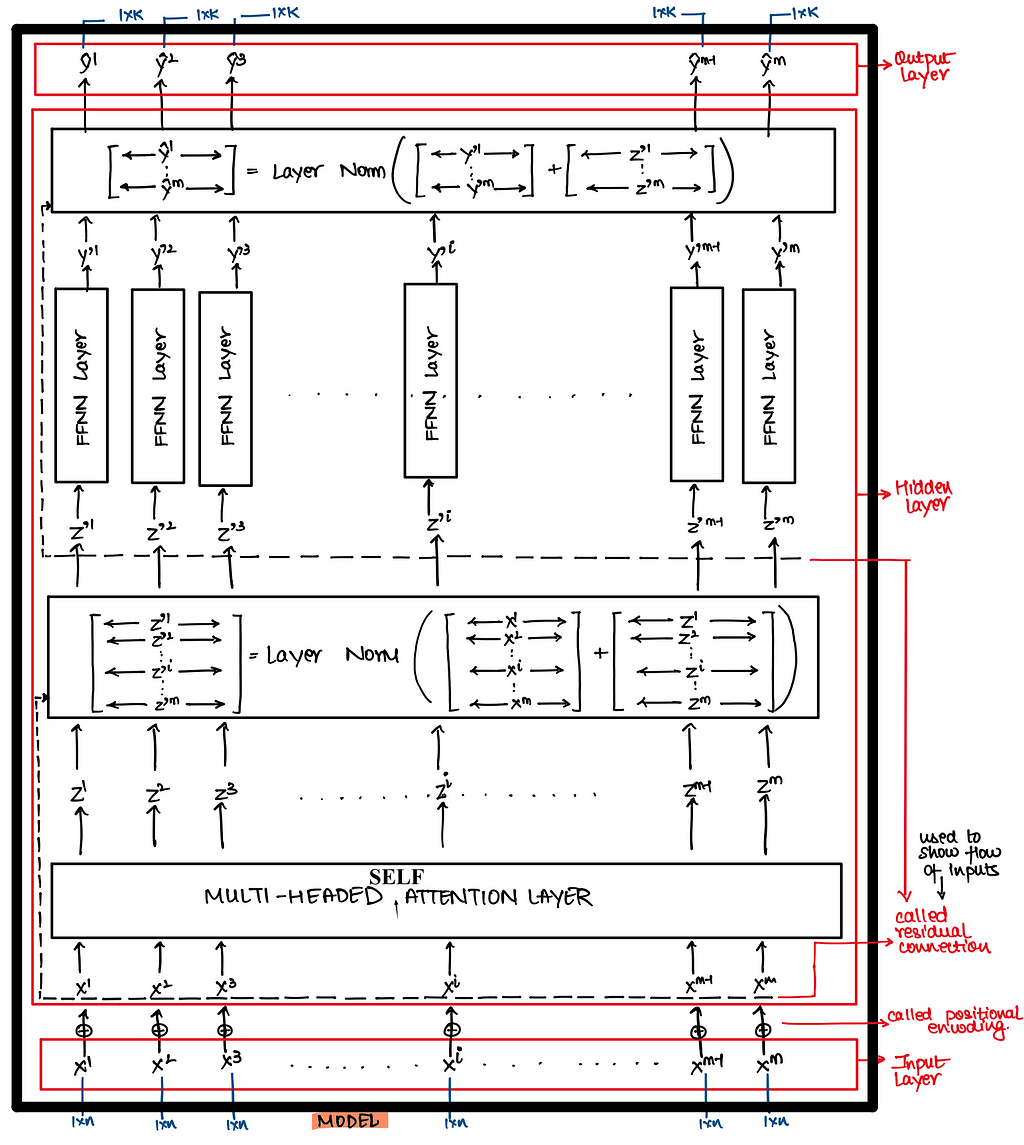
For classification task you can attach a classifier layer followed by a softmax layer in the below architecture as we have seen in LSTM for classification architecture !! Here I am not attaching a classifier at the end of the architecture to keep things simple.
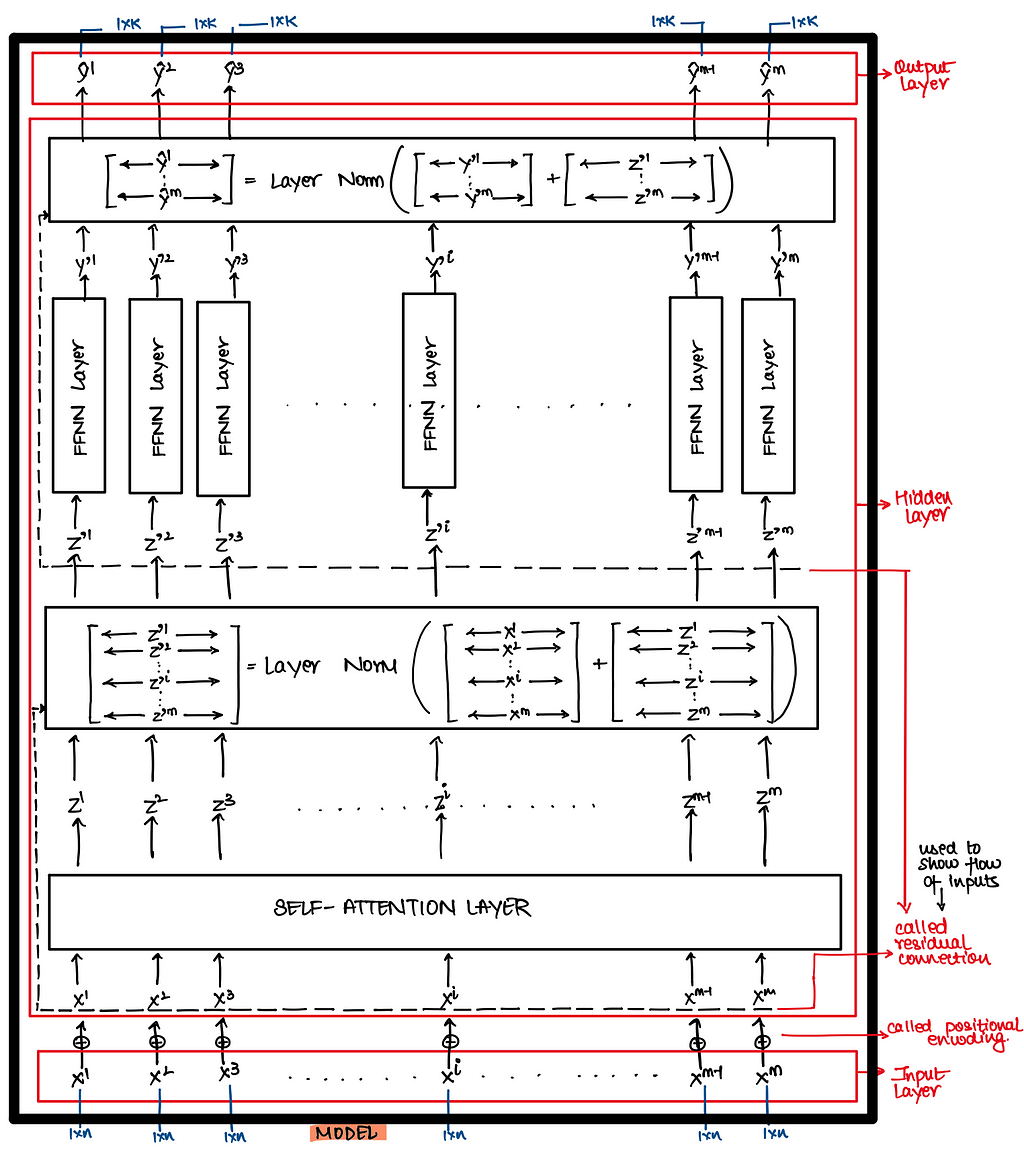
In above architecture we still don’t understand two layers i.e. Self Attention Layer and Positional Encoding Layer. Let’s try to decode them one at a time
1. Self Attention Layer :

- Self Attention Using Vector Implementation : First we will look at how to calculate self-attention using vectors for better understanding of things and then proceed to look at how it’s actually implemented using matrices
- Self Attention Using Matrix Implementation
2. Positional Encoding

Self Attention — Vector Implementation
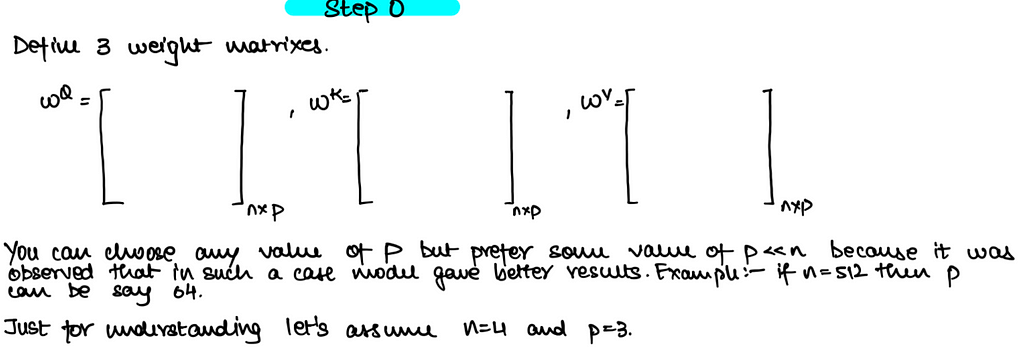
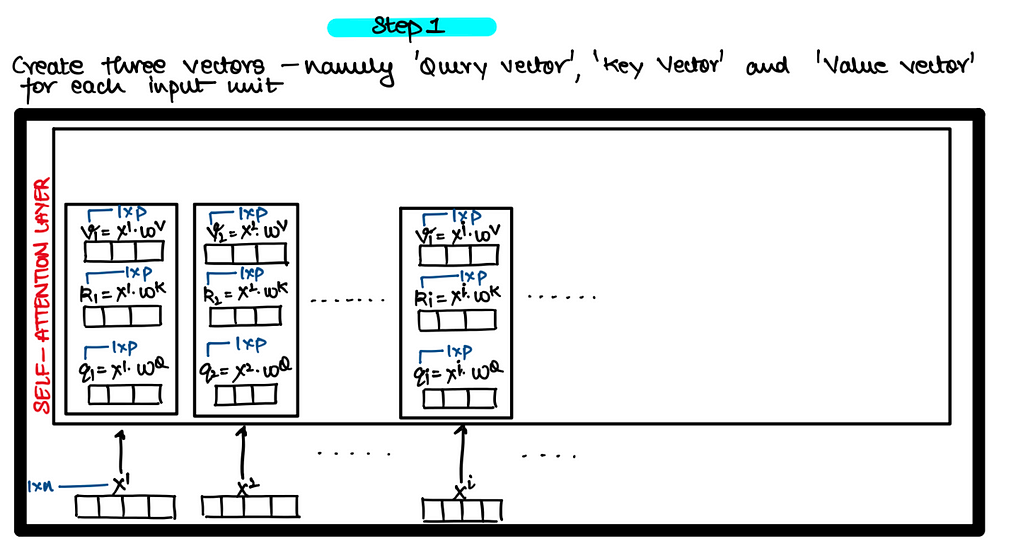
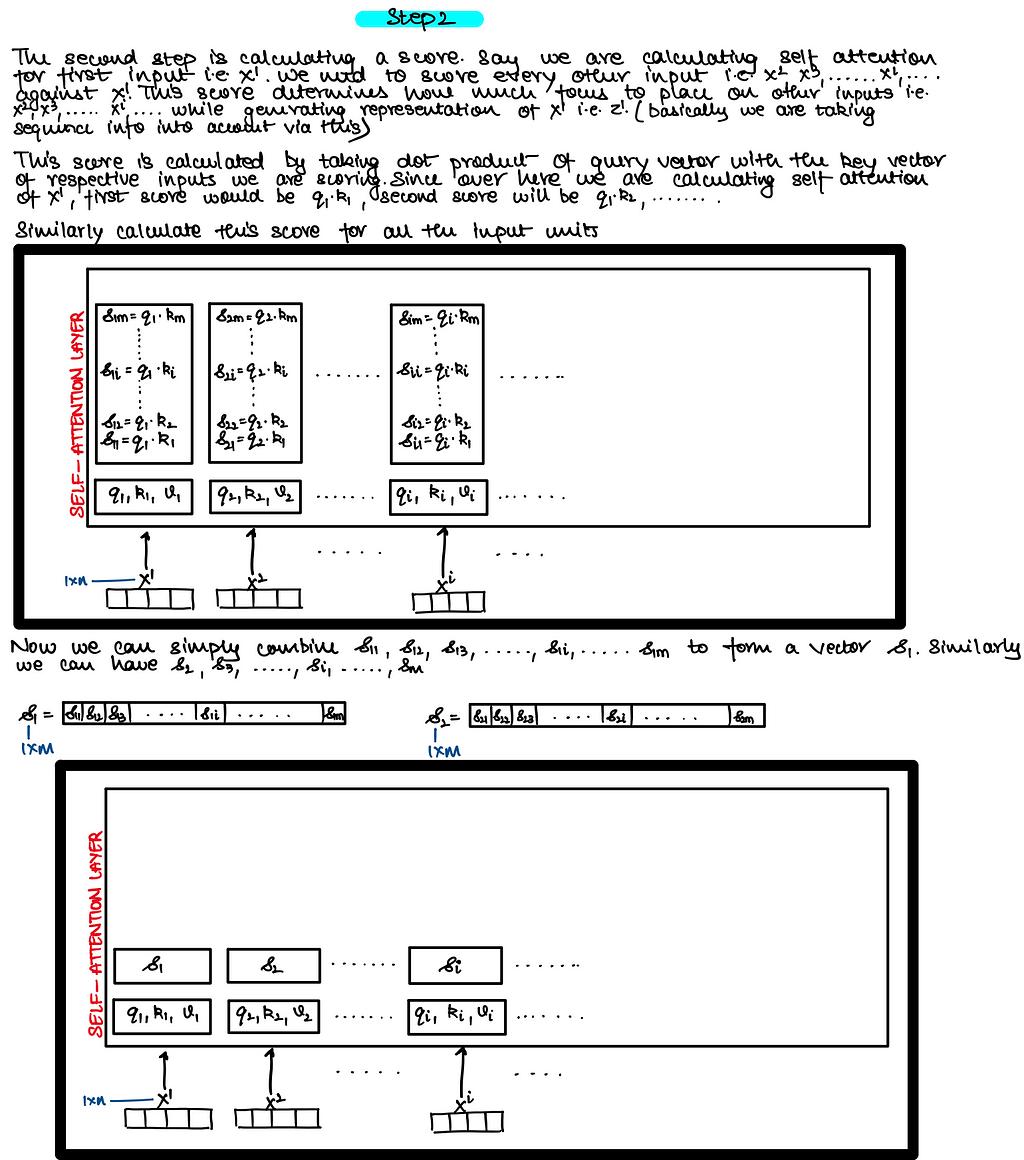
The weight vectors above i.e. Wq, Wk and Wv are nothing but FFNN so that you can project the X from one dimension to another dimension !!
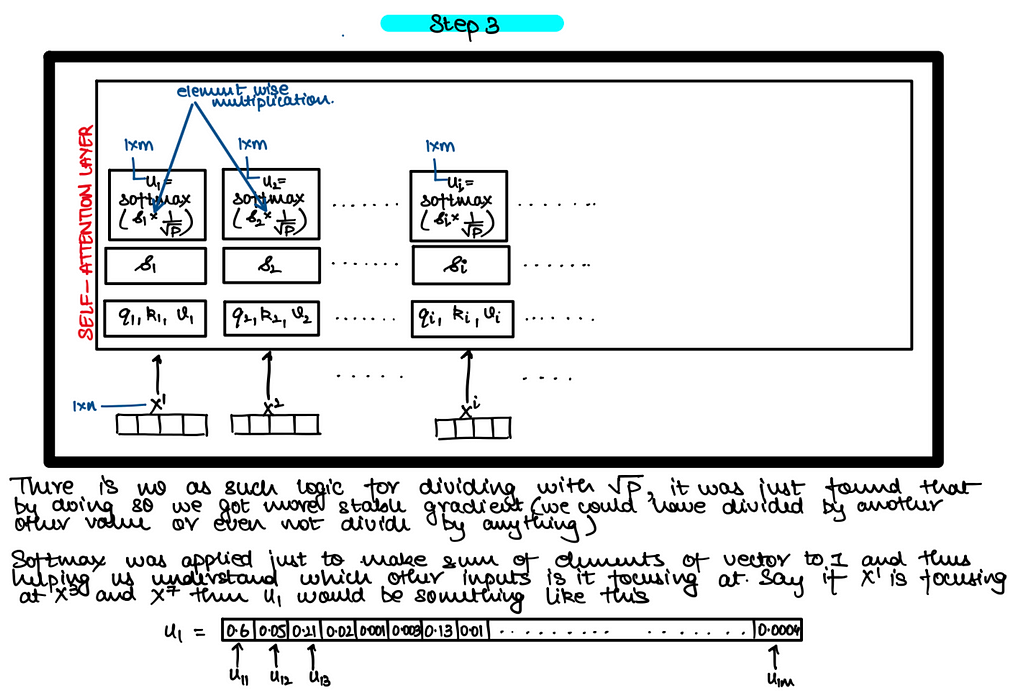
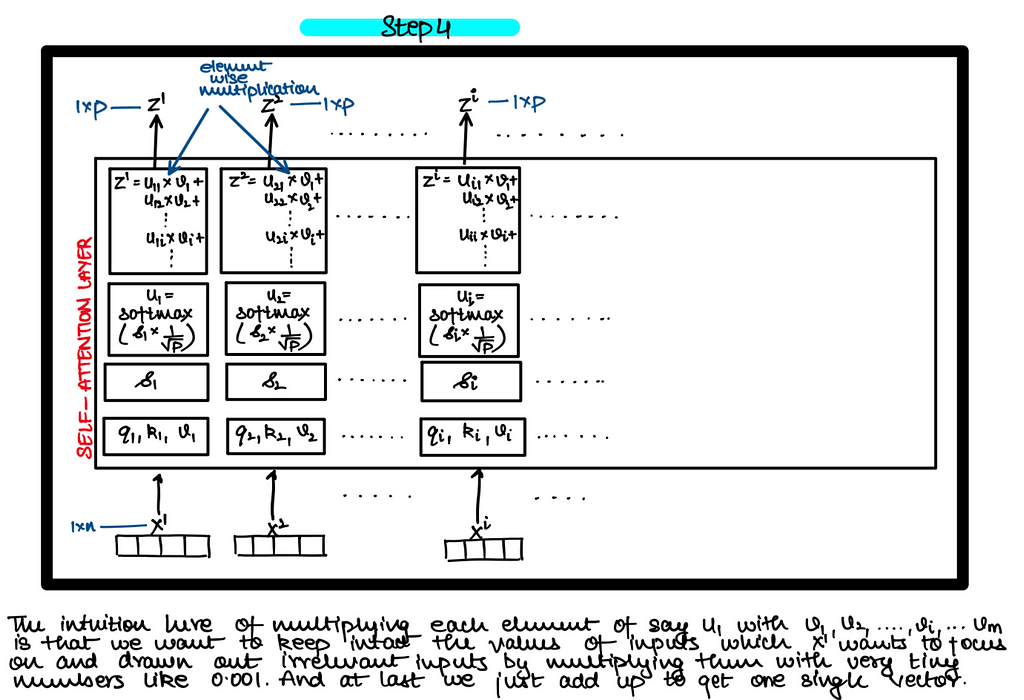

Self Attention — Matrix Implementation
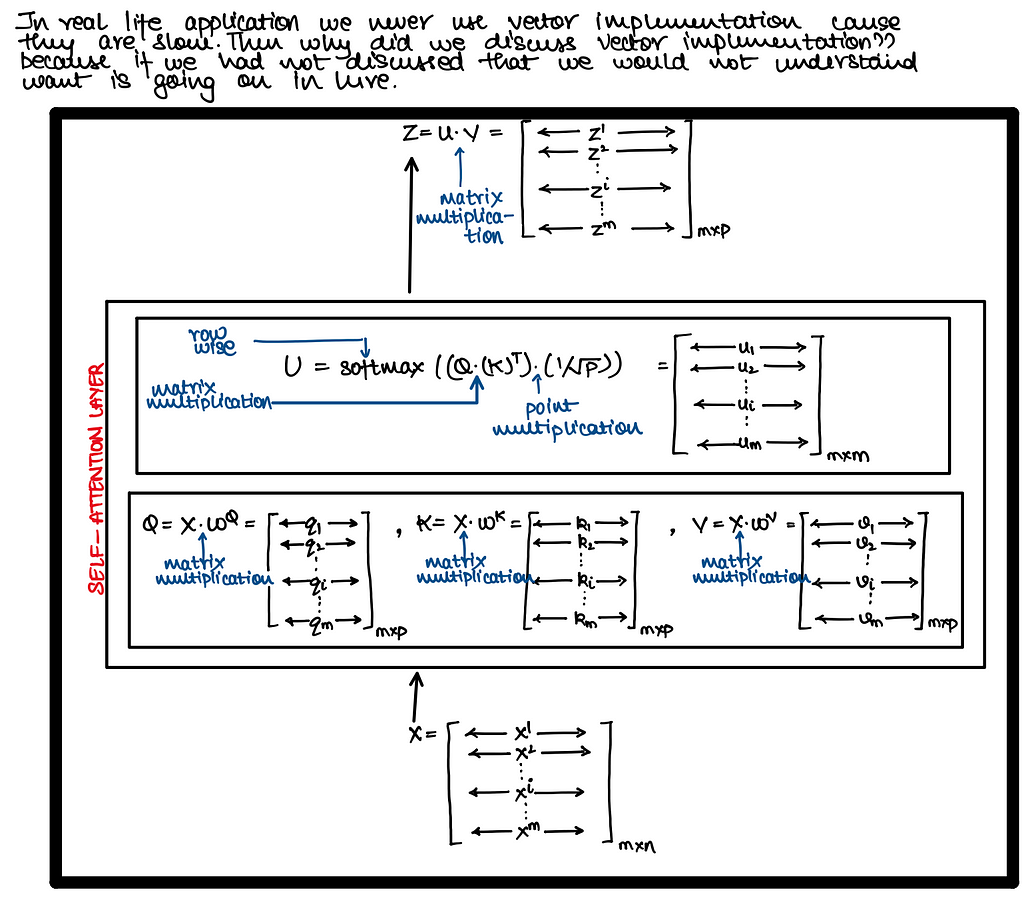

Positional Encoding
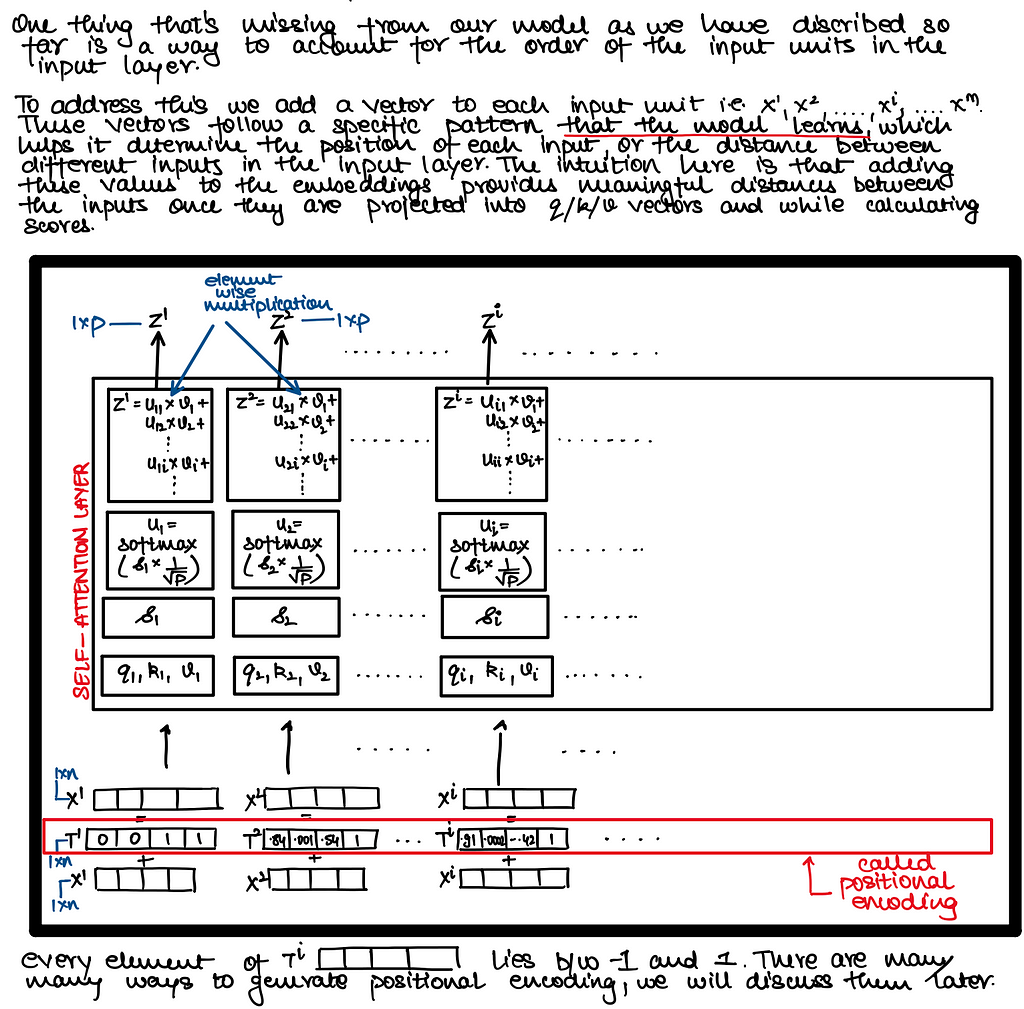
Note : Positional Encodings are not learnt!! They are just calculated once and then remain fixed
Absolute Positional Embedding - Sinusoidal Positional Embedding
class RotatoryPositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
def forward(self, x):
return x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
Relative Positional Embedding - Rotatory Positional Embedding (RoPE)
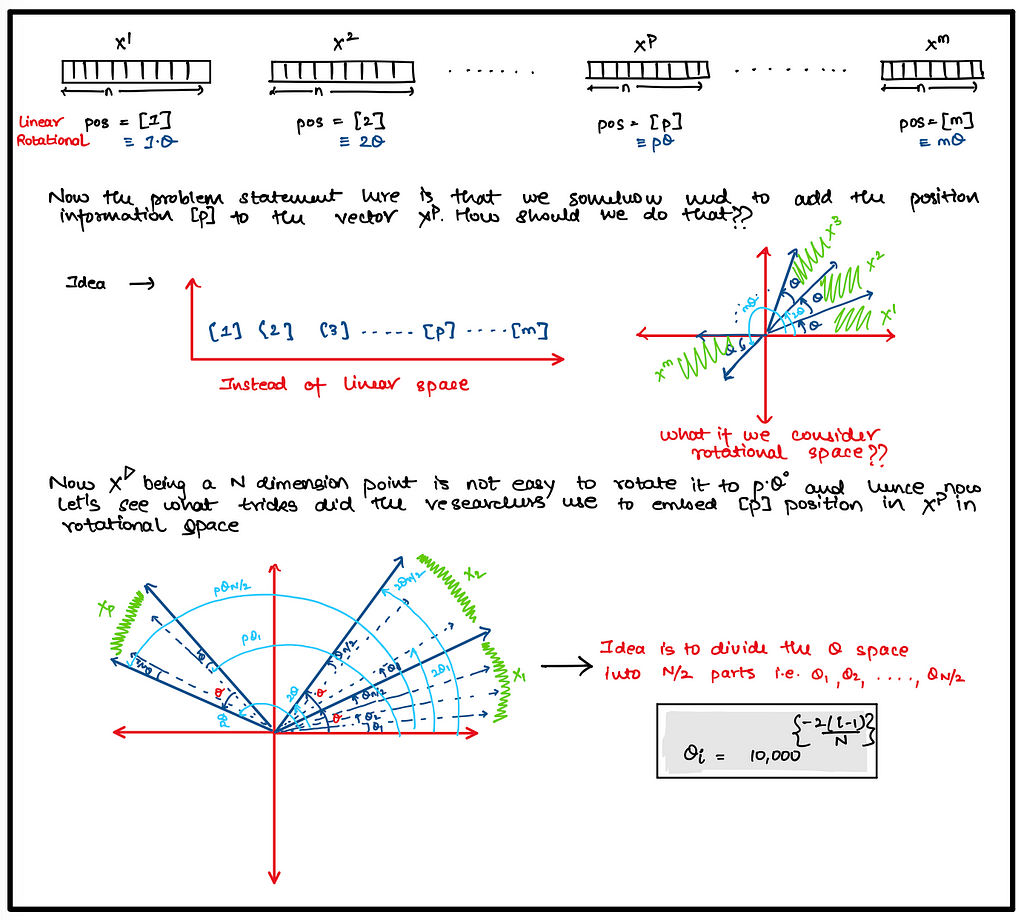
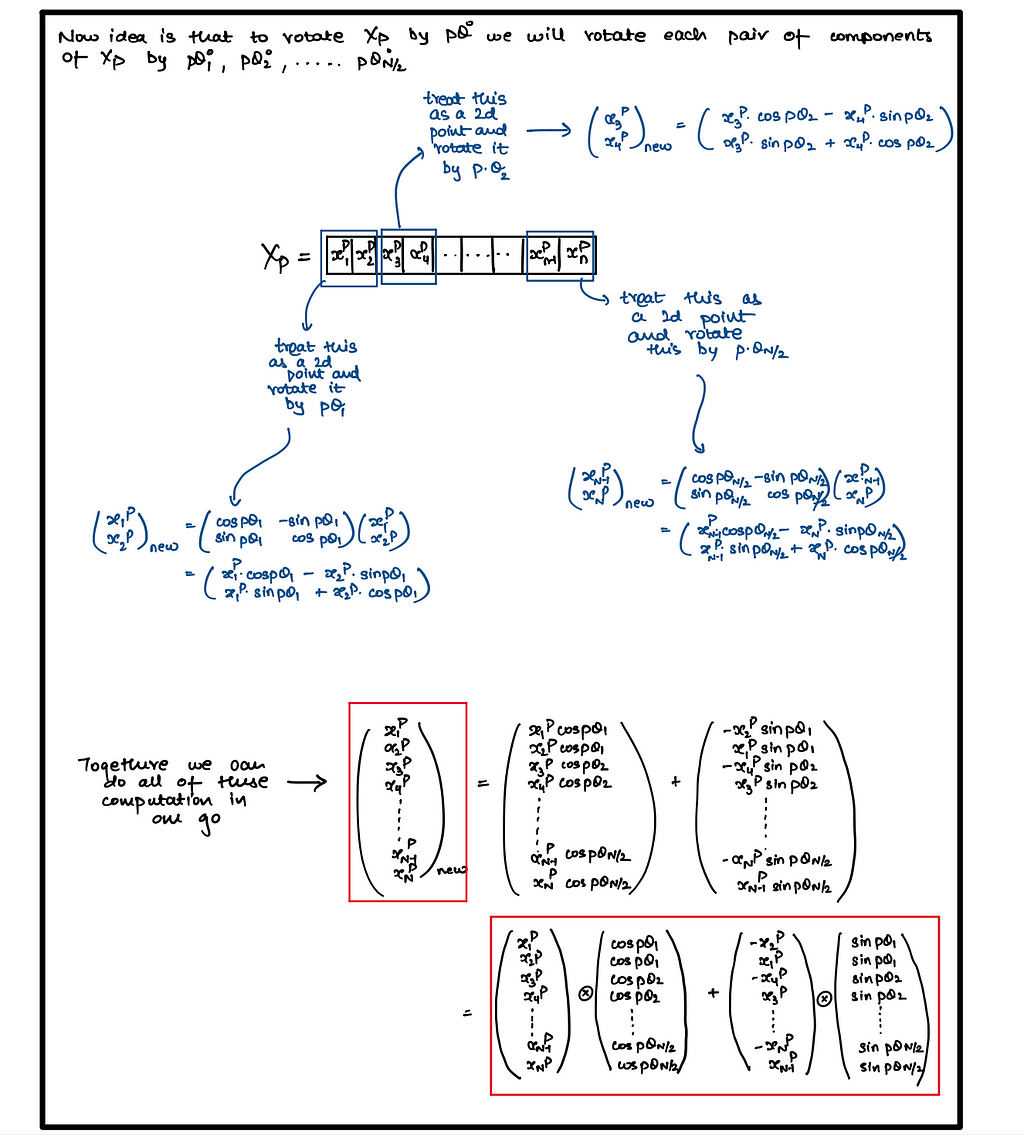
def precompute_theta_pos_frequencies(head_dim: int, seq_len: int, device: str, theta: float = 10000.0):
# As written in the paragraph 3.2.2 of the paper
# >> In order to generalize our results in 2D to any xi ∈ Rd where **d is even**, [...]
assert head_dim % 2 == 0, "Dimension must be divisible by 2"
# Build the theta parameter
# According to the formula theta_i = 10000^(-2(i-1)/dim) for i = [1, 2, ... dim/2]
# Shape: (Head_Dim / 2)
theta_numerator = torch.arange(0, head_dim, 2).float()
# Shape: (Head_Dim / 2)
theta = 1.0 / (theta ** (theta_numerator / head_dim)).to(device) # (Dim / 2)
# Construct the positions (the "m" parameter)
# Shape: (Seq_Len)
m = torch.arange(seq_len, device=device)
# Multiply each theta by each position using the outer product.
# Shape: (Seq_Len) outer_product* (Head_Dim / 2) -> (Seq_Len, Head_Dim / 2)
freqs = torch.outer(m, theta).float()
# We can compute complex numbers in the polar form c = R * exp(m * theta), where R = 1 as follows:
# (Seq_Len, Head_Dim / 2) -> (Seq_Len, Head_Dim / 2)
freqs_complex = torch.polar(torch.ones_like(freqs), freqs)
return freqs_complex
def apply_rotary_embeddings(x: torch.Tensor, freqs_complex: torch.Tensor, device: str):
# Separate the last dimension pairs of two values, representing the real and imaginary parts of the complex number
# Two consecutive values will become a single complex number
# (B, Seq_Len, H, Head_Dim) -> (B, Seq_Len, H, Head_Dim/2)
x_complex = torch.view_as_complex(x.float().reshape(*x.shape[:-1], -1, 2))
# Reshape the freqs_complex tensor to match the shape of the x_complex tensor. So we need to add the batch dimension and the head dimension
# (Seq_Len, Head_Dim/2) --> (1, Seq_Len, 1, Head_Dim/2)
freqs_complex = freqs_complex.unsqueeze(0).unsqueeze(2)
# Multiply each complex number in the x_complex tensor by the corresponding complex number in the freqs_complex tensor
# Which results in the rotation of the complex number as shown in the Figure 1 of the paper
# (B, Seq_Len, H, Head_Dim/2) * (1, Seq_Len, 1, Head_Dim/2) = (B, Seq_Len, H, Head_Dim/2)
x_rotated = x_complex * freqs_complex
# Convert the complex number back to the real number
# (B, Seq_Len, H, Head_Dim/2) -> (B, Seq_Len, H, Head_Dim/2, 2)
x_out = torch.view_as_real(x_rotated)
# (B, Seq_Len, H, Head_Dim/2, 2) -> (B, Seq_Len, H, Head_Dim)
x_out = x_out.reshape(*x.shape)
return x_out.type_as(x).to(device)

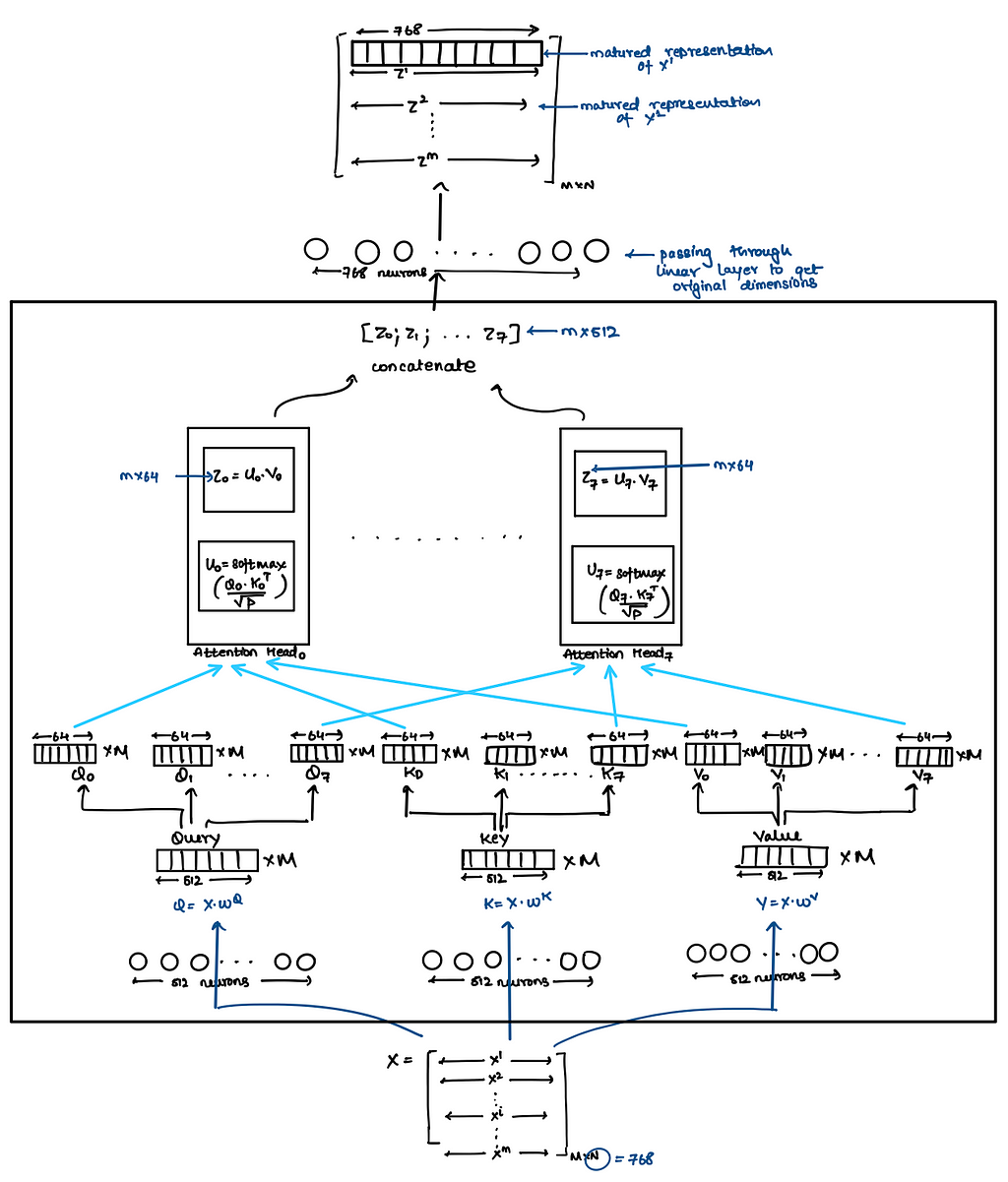
Multi Head Self Attention Transformer
Now everything remains exactly same as what we saw in above single head self attention transformers architecture except that now instead of using single-head self attention we will use multi-head self attention !!
Now everything is known over here except the multi headed attention layer. We will discuss details of this layer directly in matrix but before that let’s discuss why multi-headed attention is needed ??What advantages does it brings-in?? It expands the model’s ability to focus on different positions i.e. say while transform X^i to Z^i using just single headed self-attention it was observed that Z^i contained little bit of every other input but it was dominated by X^i. Hence we didn’t want this to happen.

Matrix Implementation
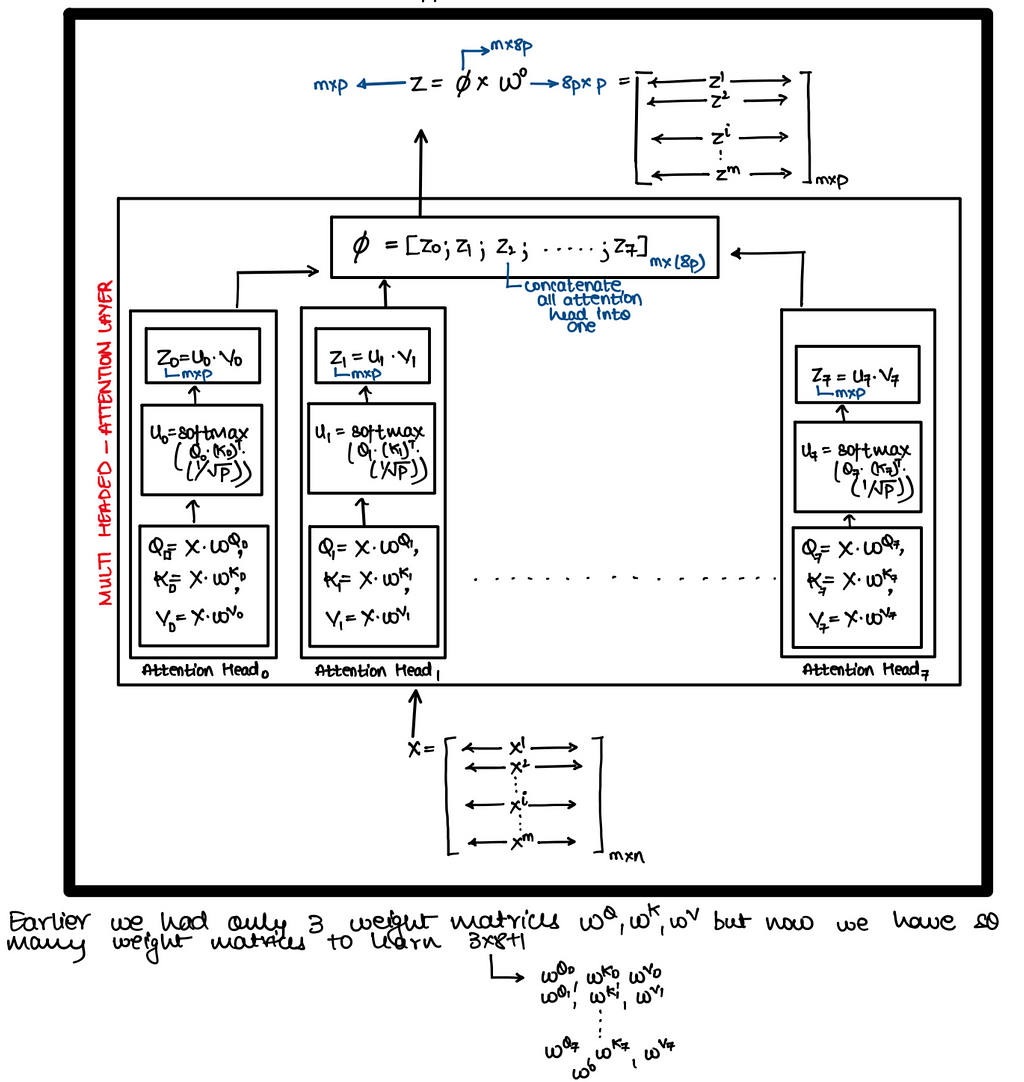
Hence in above approach we had to learn a lot of weight matrices and hence to reduce these matrices researchers used following trick
class MultiHeadedAttention(nn.Module):
def __init__(self):
super().__init__()
self.linear_1 = nn.Linear(768, 8*64, bias=True)
self.linear_2 = nn.Linear(768, 8*64, bias=True)
self.linear_3 = nn.Linear(768, 8*64, bias=True)
self.output_proj = nn.Linear(8*64, 768)
def forward(self, query, key, value):
B = x.shape[0] # X => Batch Size x M x N (=768)
'''Projecting X to get K Q and V'''
q = self.linear_1(query) # Batch Size x M x 512
k = self.linear_2(key) # Batch Size x M x 512
v = self.linear_3(value) # Batch Size x M x 512
'''Splitting'''# Batch Size x Number of Patches x Attention Dimension =>
q = rearrange(q, 'b n (n_h h_dim) -> b n_h n h_dim', n_h=8, h_dim=64) #Batch Size x M x (8 * 64) => Batch Size x 8 x M x 64
k = rearrange(k, 'b n (n_h h_dim) -> b n_h n h_dim', n_h=8, h_dim=64)
v = rearrange(v, 'b n (n_h h_dim) -> b n_h n h_dim', n_h=8, h_dim=64)
''' Calculating Attention '''
att = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(64) # B x H x N x Head Dimension @ B x H x Head Dimension x N => B x H x N x N
''' Passing Attention to Softmax'''
att = torch.nn.functional.softmax(att, dim=-1)
''' Multiplying attention and value vector'''
out = torch.matmul(att, v) # B x H x N x N @ B x H x N x Head Dimension -> B x H x N x Head Dimension
'''Concatenation'''
out = rearrange(out, 'b n_h n h_dim -> b n (n_h h_dim)') # B x N x (8 * 64) => B x N x 512
'''Projecting back to original dimension'''
out = self.output_proj(out)
return out, att
class TransformerEncoderLayer(nn.Module):
def __init__(self):
super().__init__()
# Attention Block
self.att_norm = nn.LayerNorm(768, elementwise_affine = False, eps = 1E-6)
self.attn_block = MultiHeadedAttention()
'''
Instead of self implementation, you can use pytorch based implementation
also for attention layer
nn.MultiheadAttention(embed_dim=768, num_heads=8, batch_first=True)
'''
# FFNN block
self.ff_norm = nn.LayerNorm(768, elementwise_affine = False, eps = 1E-6)
self.mlp_block = nn.Sequential( nn.Linear(768, 4 * 768),
nn.GELU(approximate='tanh'),
nn.Linear(4 * 768, 768)
)
def forward(self, x):
# attention block
attn_norm_output = self.att_norm(x)
attn_output, _ = self.attn_block(query = attn_norm_output,
key = attn_norm_output,
value = attn_norm_output)
out = x + attn_output
# FFNN block
mlp_norm_output = self.ff_norm(out)
out = out + self.mlp_block(mlp_norm_output)
return out
transformer_encoder_layer = TransformerEncoderLayer()
'''
Instead of implementing your own transformer layer you can use this pytorch
implementation too !!
nn.TransformerEncoderLayer(d_model=768,
nhead=8,
dim_feedforward=4 * 768,
dropout=0.1,
activation="gelu",
batch_first=True,
norm_first=True)
'''

Visualizing Multi Head Self Attention

Implement Transformers (Bidirectional) from Scratch in Pytorch for Sequence Classification was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Sarvesh Khetan
Sarvesh Khetan | Sciencx (2025-01-10T02:25:12+00:00) Implement Transformers (Bidirectional) from Scratch in Pytorch for Sequence Classification. Retrieved from https://www.scien.cx/2025/01/10/implement-transformers-bidirectional-from-scratch-in-pytorch-for-sequence-classification/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
