This content originally appeared on HackerNoon and was authored by Anchoring
:::info Authors:
(1) Jongmin Lee, Department of Mathematical Science, Seoul National University;
(2) Ernest K. Ryu, Department of Mathematical Science, Seoul National University and Interdisciplinary Program in Artificial Intelligence, Seoul National University.
:::
1.1 Notations and preliminaries
2.1 Accelerated rate for Bellman consistency operator
2.2 Accelerated rate for Bellman optimality opera
5 Approximate Anchored Value Iteration
6 Gauss–Seidel Anchored Value Iteration
7 Conclusion, Acknowledgments and Disclosure of Funding and References
3 Convergence when y=1
Undiscounted MDPs are not commonly studied in the DP and RL theory literature due to the following difficulties: Bellman consistency and optimality operators may not have fixed points, VI is a nonexpansive (not contractive) fixed-point iteration and may not convergence to a fixed point even if one exist, and the interpretation of a fixed point as the (optimal) value function becomes unclear when the fixed point is not unique. However, many modern deep RL setups actually do not use discounting, [2] and this empirical practice makes the theoretical analysis with γ = 1 relevant.
\ In this section, we show that Anc-VI converges to fixed points of the Bellman consistency and optimality operators of undiscounted MDPs. While a full treatment of undiscounted MDPs is beyond the scope of this paper, we show that fixed points, if one exists, can be found, and we therefore argue that the inability to find fixed points should not be considered an obstacle in studying the γ = 1 setup.
\ We first state our convergence result for finite state-action spaces.
\
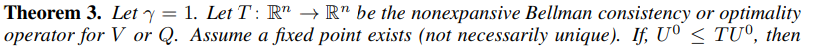
\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::

\ [3] Well-definedness of T requires a σ-algebra on state and action spaces, expectation with respect to transition probability and policy to be well defined, boundedness and measurability of the output of Bellman operator, etc.
This content originally appeared on HackerNoon and was authored by Anchoring
Anchoring | Sciencx (2025-01-14T22:56:32+00:00) Why Anc-VI is Crucial for Undiscounted Reinforcement Learning. Retrieved from https://www.scien.cx/2025/01/14/why-anc-vi-is-crucial-for-undiscounted-reinforcement-learning/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
