This content originally appeared on HackerNoon and was authored by Hierarchy
Table of Links
\ Appendix A. Appendix to Section 2 & Appendix B. Appendix to Section 3
Appendix C. Appendix to Section 4
Appendix D. Appendix to Section 5
4. Rating maps
We use the framework of [25] to handle covering. It is based on objects called rating maps. They “rate” covers. For each lattice C, each rating map ρ and each language L, we define the optimal C-covers of L for ρ. We reduce C-covering to the computation of optimal C-covers.
\ 4.1. Multiplicative rating maps. A semiring is a tuple (R, +, ·) where R is a set and “+” and “·” are two binary operations called addition and multiplication, which satisfy the following axioms:
\ • (R, +) is a commutative monoid, whose identity element is denoted by 0R.
\ • (R, ·) is a monoid, whose identity element is denoted by 1R.
\ • Distributivity: for r, s, t ∈ R, r · (s + t) = (r · s) + (r · t) and (r + s) · t = (r · t) + (s · t).
\ • 0R is a zero for (R, ·): 0R · r = r · 0R = 0R for every r ∈ R.
\ A semiring R is idempotent when r + r = r for all r ∈ R (there is no additional constraint on the multiplication). Given an idempotent semiring (R, +, ·), we define a relation ≤ over R: for all r, s ∈ R, we let r ≤ s if and only if r + s = s. One can check that ≤ is a partial order compatible with both addition and multiplication and that every morphism between two commutative and idempotent monoids is increasing for this ordering.
\

\ Remark 24. As the adjective “multiplicative” suggests, there exists a more general notion of “rating map”. We do not use this notion, see [25] for the general framework.
\

\ Lemma 25. Let C be a lattice. For every language L and every multiplicative rating map ρ, there exists an optimal C-cover of L for ρ.
\ Clearly, given a lattice C, a language L and a multiplicative rating map ρ, all optimal C-covers of L for ρ have the same ρ-imprint. Hence, this unique ρ-imprint is a canonical object for C, L and ρ. We call it the C-optimal ρ-imprint on L and we write it IC [L, ρ]. That is IC [L, ρ] = I[ρ](K) for every optimal C-cover K of L for ρ.
\ 4.2. Application to covering. Deciding C-covering for a fixed class C boils down to finding an algorithm that computes C-optimal imprints. Indeed, if C is a Boolean algebra, we have the following statement of [25].
\

\ The converse of Proposition 26 is also true: if C-covering is decidable, then one can compute the C-optimal imprints. We present a proof in Appendix C.
\

\
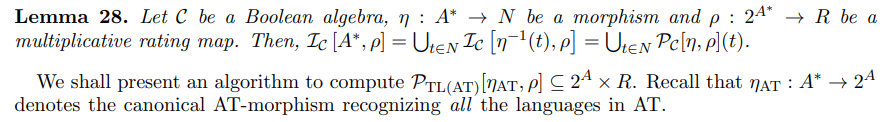
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Authors:
(1) Thomas Place;
(2) Marc Zaitoun.
:::
\
This content originally appeared on HackerNoon and was authored by Hierarchy
Hierarchy | Sciencx (2025-01-31T02:17:22+00:00) Rating Maps: The Framework That We Used. Retrieved from https://www.scien.cx/2025/01/31/rating-maps-the-framework-that-we-used/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
