This content originally appeared on HackerNoon and was authored by Exoplanetology Tech: Research on the Study of Planets
Table of Links
Clocks at Earth-Moon Lagrance Points
4.1 Clock at Lagrange point L1
\ Appendix 1: Fermi Coordinates with Origin at the Center of the Moon
Appendix 2: Construction of Freely Falling Center of Mass Frame
Appendix 3: Equations of Motion of Earth and Moon
Appendix 4: Comparing Results in Rotating and Non-Rotating Coordinate Systems
Acknowledgments and References
\
3. CLOCK RATE DIFFERENCES BETWEEN EARTH AND MOON
The Earth and the Moon orbit around their mutual center of mass in different Keplerian orbits. Meanwhile, the center of mass of the Earth-Moon system orbits around the Sun in an approximately Keplerian orbit. To calculate the rate differences between clocks on Earth and on the Moon, a fictitious locally freely-falling inertial frame is introduced at the Earth-Moon center of mass. This makes it convenient to calculate the proper times elapsed on moving clocks in terms of Keplerian motions of the Earth and the Moon. The Sun’s contribution is only tidal effects. If we omit the tidal potential of the Sun, the scalar invariant takes a simple form (Appendix 2)
\
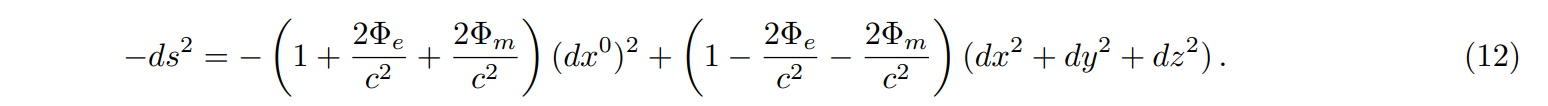
\ Consider a clock fixed on the surface of the rotating geoid of Earth. Since the geoid is a surface of approximate hydrostatic equilibrium, if such clocks are viewed from the local inertial frame they beat at the same rate, which can be evaluated at the equator. The proper time on the Earth-based clock becomes
\
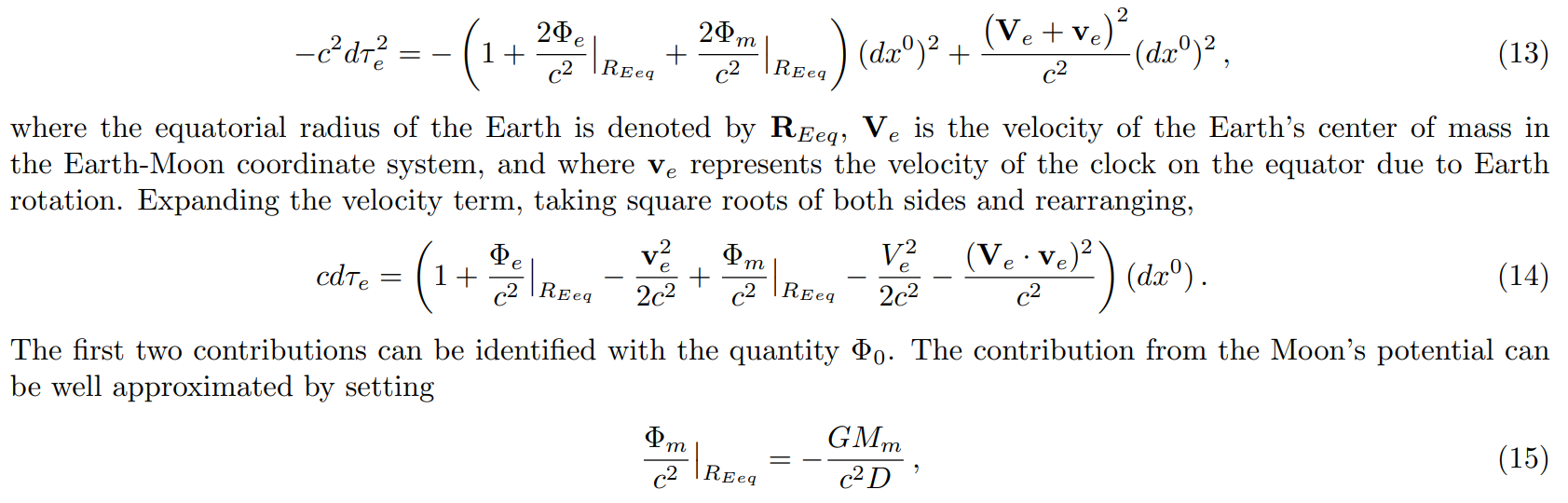
\ The first two contributions can be identified with the quantity Φ0. The contribution from the Moon’s potential can be well approximated by setting
\

\ where D is the Earth-Moon distance. The dot product term between velocities will depend on the specific position of the clock and will vary with a daily period; this variation is similar to the corrections to the gravitational potential contribution from the Moon arising from the fact that the clock is not at the center of the Earth. Omitting such contributions give
\
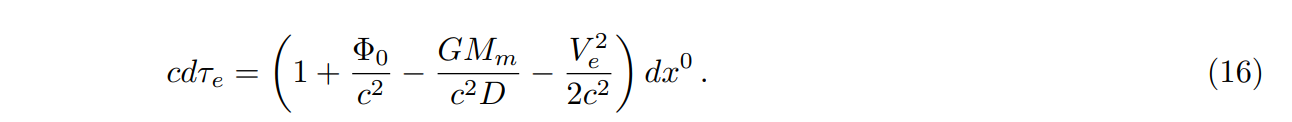
\ A similar argument applied to a clock fixed on the rotating Moon’s surface of hydrostatic equilibrium gives the proper time
\

\
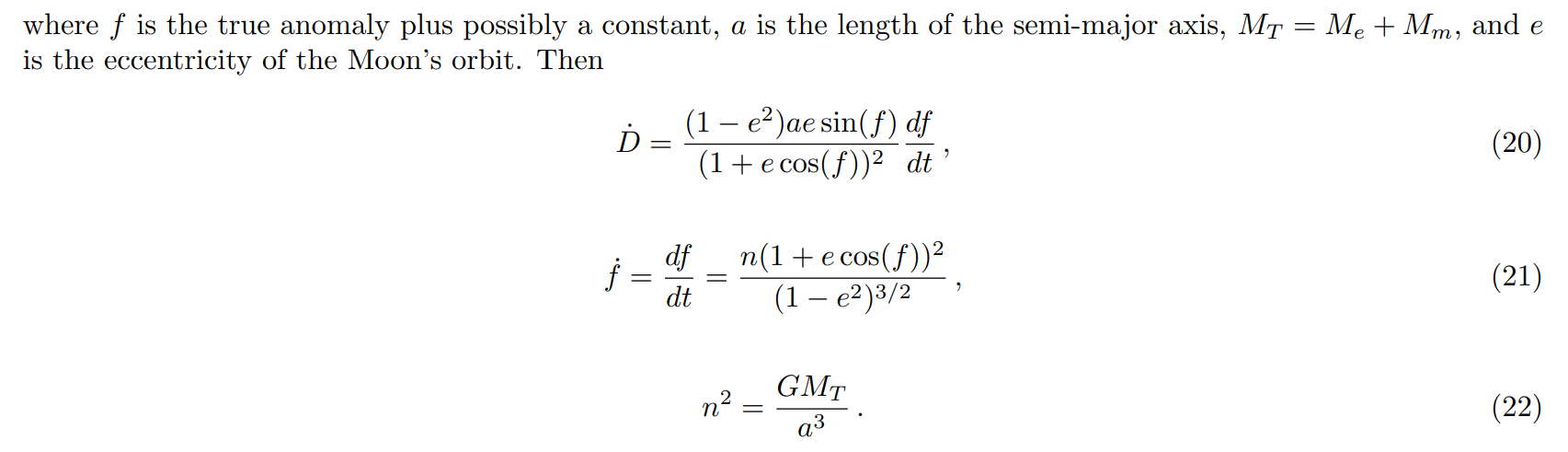
\ The following combination of quantities occurs frequently and can be reduced to a simpler expression
\
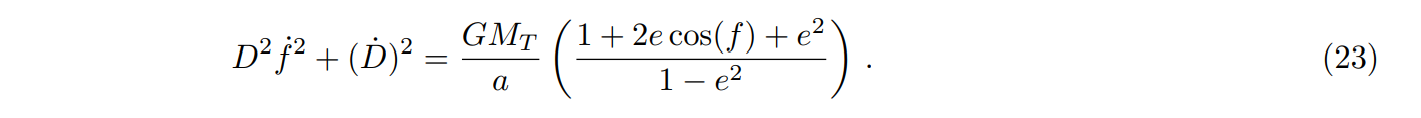
\

\ The difference of squares of velocities is then
\
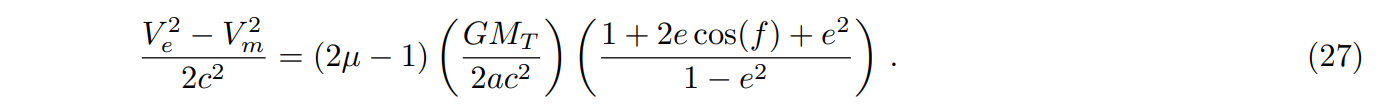
\ Using Eq.(27) in Eq.(18), we obtain
\
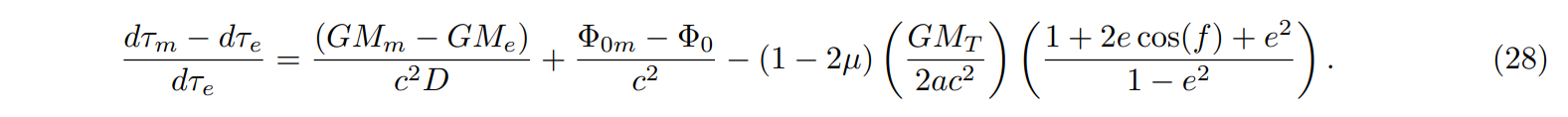
\

\

\ This term will have a period of approximately 27 days. Cross terms between velocities of the center of mass and rotational velocities have been omitted. One such term is
\
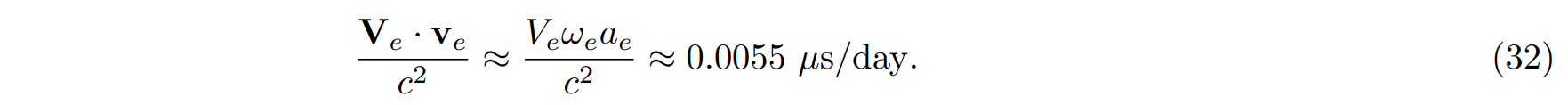
\ This contribution will also vary with the rotation period of the Earth. Another such term is
\
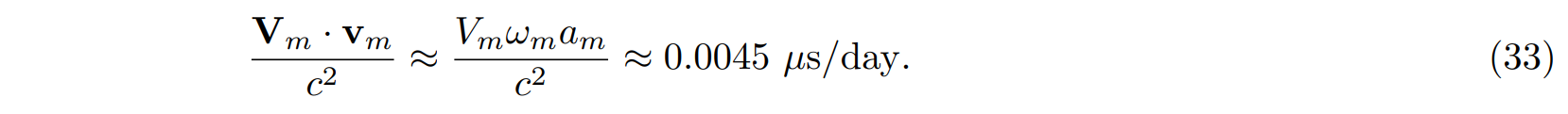
\ Since the Moon is tidally locked to the Earth, its center of mass velocity and the velocity of a clock on the selenoid will be highly correlated. Therefore, this term might give rise to a constant long-term average. Omitting the position-dependent terms, we have used the constants listed in Table I to evaluate the constant contribution and the amplitude of the periodic term. We find:
\

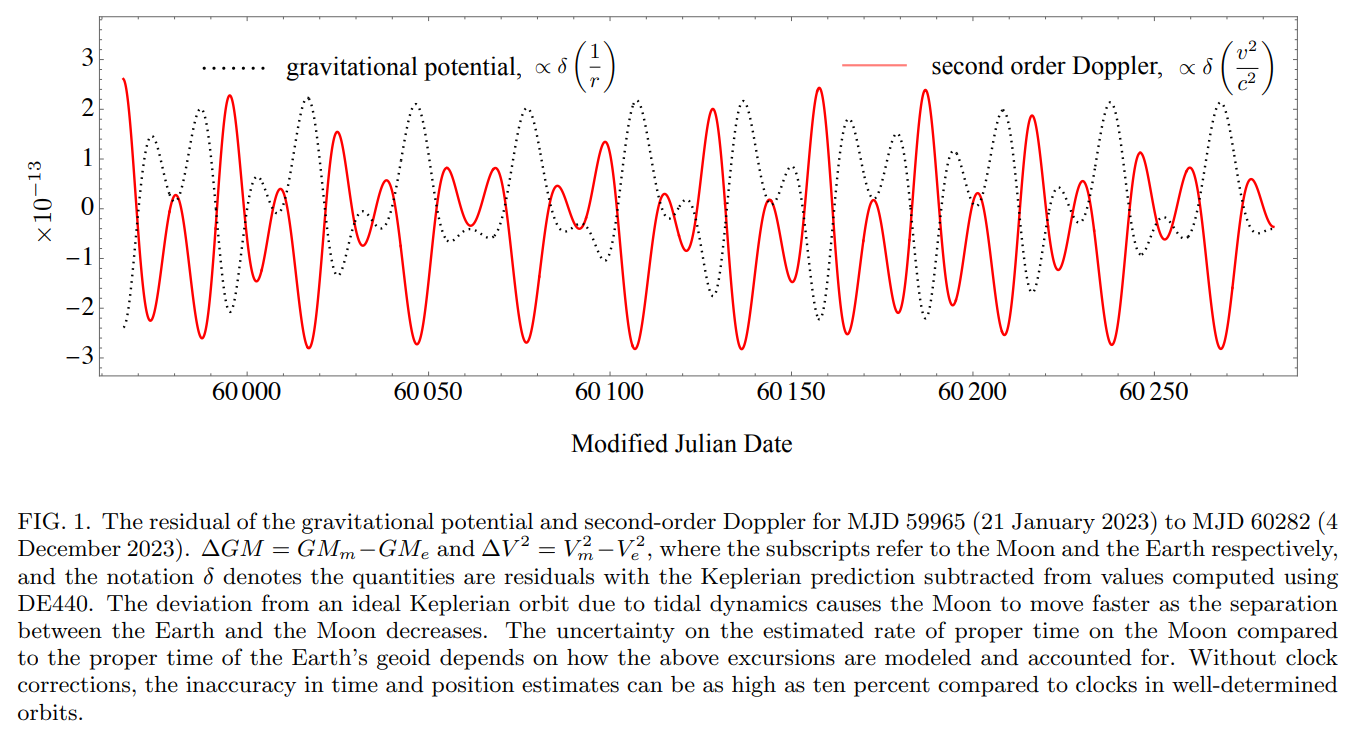
\ None of the above estimates include tidal effects. This omission is because as a tidal force pushes back and forth on a satellite, two other side effects have to be accounted for. These are a change in the position of the satellite that entails a change in the gravitational potential of the body about which the satellite is orbiting and a change in the velocity of the satellite clock that changes its second-order Doppler shift. The residuals of the gravitational potential and second-order Doppler shift for the Earth-Moon system obtained by subtracting the Keplerian model from that obtained from DE440 are graphed in Fig. 1. Previous work on such problems has shown that these changes are of similar orders of magnitude. Summarizing, there are three contributions to the frequency shift of a clock in a satellite that are of similar orders of magnitude: (1) the perturbing tidal potential itself; (2) the perturbed position that changes the contribution from the main potential; (3) the perturbed velocity that changes the time dilation contribution. Although the perturbing tidal potential can easily be estimated, calculating the other two contributions is more complicated. When the Keplerian model is compared with DE440 ephemerides, the effects of solar tides are plotted in Fig. 2.
\

\
\ It might appear that the second-order Doppler contribution to the rate difference depends on the coordinate system used. In the center-of-mass coordinates, a difference of squares of velocities appears, but in a system in which the Earth is at rest, the square of the relative velocity appears. Appendix 4 shows that contributions from the centrifugal potential, which occurs in a rotating coordinate system resolve the apparent discrepancy.
\
:::info Authors:
(1) Neil Ashby, National Institute of Standards and Technology, Boulder, CO 80305 (Neil.Ashby@Colorado.Edu);
(2) Bijunath R. Patla, National Institute of Standards and Technology, Boulder, CO 80305 (bijunath.patla@nist.gov).
:::
:::info This paper is available on arxiv under CC0 1.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Exoplanetology Tech: Research on the Study of Planets
Exoplanetology Tech: Research on the Study of Planets | Sciencx (2025-02-25T22:07:35+00:00) The Role of Gravity and Motion in Space-Time Coordination. Retrieved from https://www.scien.cx/2025/02/25/the-role-of-gravity-and-motion-in-space-time-coordination/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
