This content originally appeared on HackerNoon and was authored by Linearization Technology
Table of Links
2. Mathematical Description and 2.1. Numerical Algorithms for Nonlinear Equations
2.4. Matrix Coloring & Sparse Automatic Differentiation
3.1. Composable Building Blocks
3.2. Smart PolyAlgortihm Defaults
3.3. Non-Allocating Static Algorithms inside GPU Kernels
3.4. Automatic Sparsity Exploitation
3.5. Generalized Jacobian-Free Nonlinear Solvers using Krylov Methods
4. Results and 4.1. Robustness on 23 Test Problems
4.2. Initializing the Doyle-Fuller-Newman (DFN) Battery Model
4.3. Large Ill-Conditioned Nonlinear Brusselator System
3.4. Automatic Sparsity Exploitation
Symbolic sparsity detection has a high overhead for smaller systems with well-defined sparsity patterns. We provide an approximate algorithm to determine the Jacobian sparsity pattern in those setups. We compute the dense Jacobian for 𝑛 randomly generated inputs to approximate the pattern. We take a union over the non-zero elements of Jacobian to obtain the Sparsity Pattern. As evident, computing the sparsity pattern costs 𝑛 times the cost of computing the dense Jacobian, typically via automatic forward mode differentiation.
\ Approximate sparsity detection has poor scaling beyond a certain problem size, as evident from Figure 10. Similar to the shortcomings of other numerical sparsity detection software [43, 44], our method fails to accurately predict the sparsity pattern in the presence of state-dependent branches and might over-predict or under-predict sparsity due to floating point errors. Regardless, we observe in Figure 10 that approximate sparsity detection is extremely efficient for moderately sized problems. In addition to computing the Jacobian faster, sparsity detection enables us to sparse linear solvers that are significantly more efficient than solving the equivalent large dense linear systems [Subsection 4.3].
\
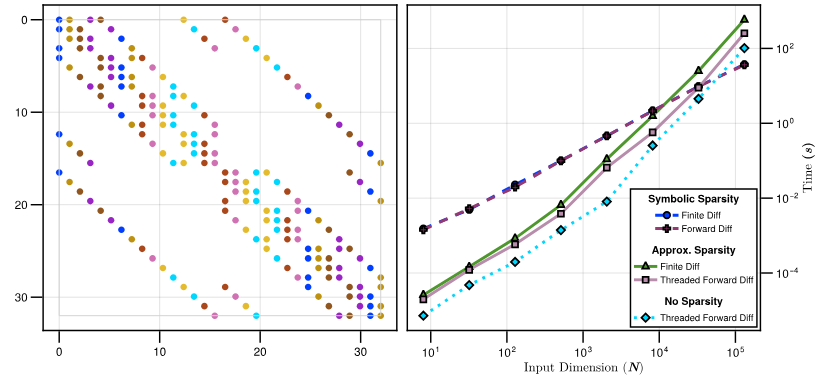
\ sparsity detection techniques will outperform other techniques. Finally, for large systems, using exact symbolic sparsity detection followed by colored AD is the most efficient.
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Authors:
(1) AVIK PAL, CSAIL MIT, Cambridge, MA;
(2) FLEMMING HOLTORF;
(3) AXEL LARSSON;
(4) TORKEL LOMAN;
(5) UTKARSH;
(6) FRANK SCHÄFER;
(7) QINGYU QU;
(8) ALAN EDELMAN;
(9) CHRIS RACKAUCKAS, CSAIL MIT, Cambridge, MA.
:::
\
This content originally appeared on HackerNoon and was authored by Linearization Technology
Linearization Technology | Sciencx (2025-03-27T00:25:03+00:00) Automatic Sparsity Detection for Nonlinear Equations: What You Need to Know. Retrieved from https://www.scien.cx/2025/03/27/automatic-sparsity-detection-for-nonlinear-equations-what-you-need-to-know/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
