This content originally appeared on Bits and Pieces - Medium and was authored by Yogi Paturu
Recursive and iterative implementations of pre-order, in-order, and post-order traversals
Contents
- What is depth first search?
- What are pre-order, in-order, and post-order traversals?
- Which of the three searches traverses a binary search tree in ascending order?
- Can you imagine the output of each of the three traversals?
- Implement a recursive pre-order depth first search.
- Implement a recursive in-order depth first search.
- Implement a recursive post-order depth first search.
- What are the trade offs for a recursive depth first search?
- What data structure is used for iterative depth first searches?
- Implement an iterative pre-order depth first search.
- Implement an iterative in-order depth first search.
- Implement an iterative post-order depth first search.
Depth-first search, as opposed to breadth first search, of a binary tree is a form of search that goes from the root to height of the tree before backtracking and repeating to paths that have yet to bee explored.
Consider pushing values of the following binary search tree as nodes are traversed depth-first. These traversals, consequently the pushes, can be done in the following ways: pre-order, in-order, and post-order.
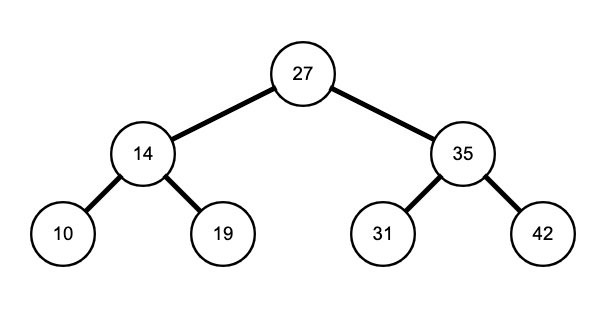
Traversal orders are as follows:
- Pre-order: parent → left child → right child
- In-order: left child → parent → right child
- Post-order: left child → right child → parent
Note that the prefix illustrates when the parent is visited. This is a mental shortcut of remembering the associated orders: the parent is visited before the children in pre-order, the parent is visited between the children in in-order, and the parent is visited after the children in post-order.
The outputs are as follows:
- Pre-order: [27, 14, 10, 19, 35, 31, 42]
- In-order: [10, 14, 19, 27, 31, 35, 42]
- Post-order: [10, 19, 14, 31, 42, 35, 27]
For binary search trees, in-order traversal is special, because it visits nodes in ascending order (i.e., in order). This is a noteworthy mental shortcut! In fact, if the in-order traversal of a binary tree is not ascending, the tree is by definition not a binary search tree.
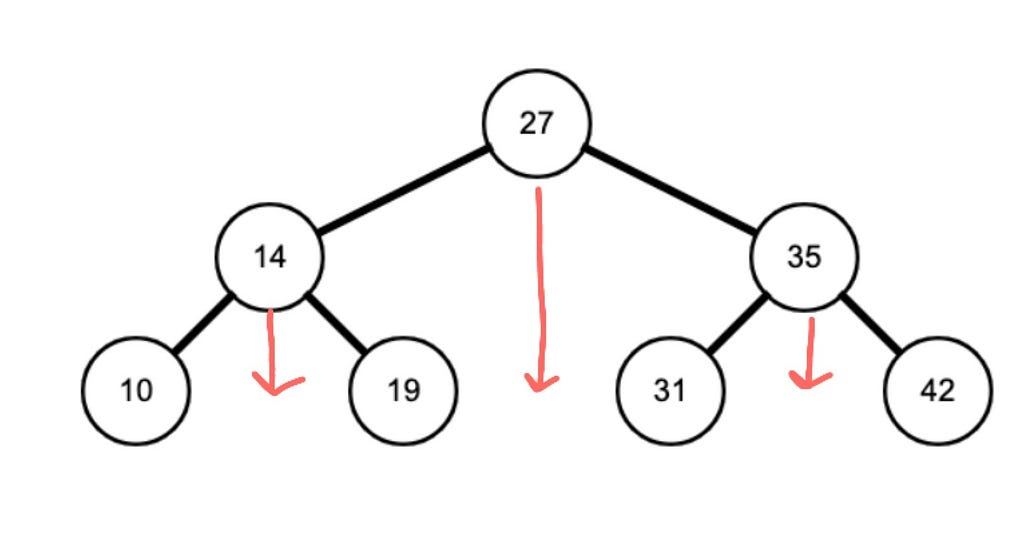
A way to imagine the output of an in-order traversal is building falling straight down. Can you see it below?
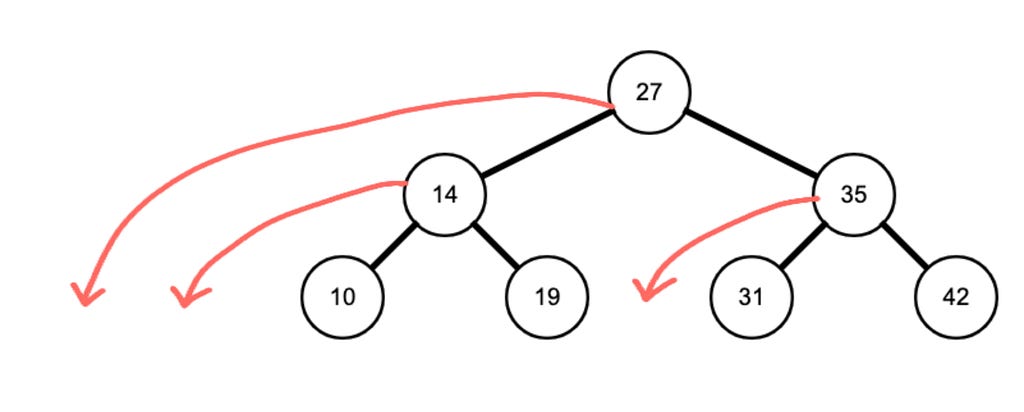
A way to mentally imagine the output of a pre-order traversal is by imagining the binary search tree as the tallest building in the world falling to the left. Because it’s so tall, the top falls all the way to the left. As it falls, the top of the building topples left, and it grabs its two pillars as it falls — finally falling to the left. The higher the node, the more it falls to the left. The base doesn’t move. Can you see it below?
Imagine the same thing happening for post-order but to the right. Can you see it below?
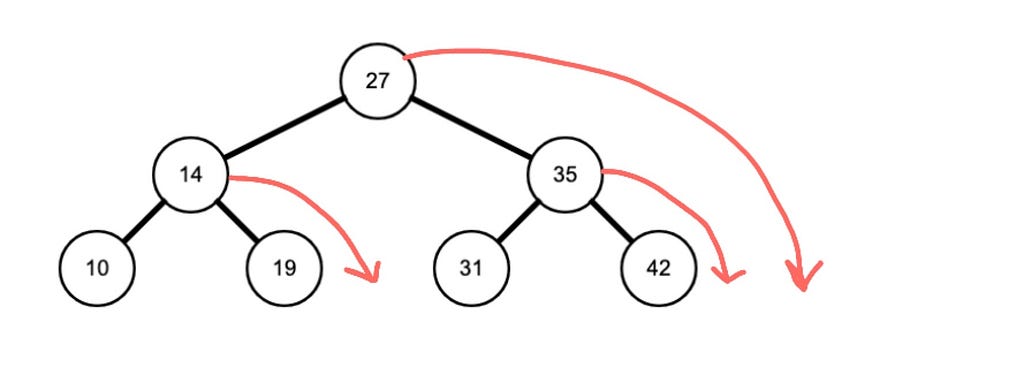
Visualizations of the outputs guide which of the three searches to implement in a given problem. Furthermore, while post-order and in-order are a way to traverse bottom-up the tree, pre-order is a way to traverse top-down.
There are two ways to implement depth-first search: recursively and iteratively.
While the recursive implementation is concise and clear, it always causes a stack overflow if the number of height of the tree is greater than the call stack. On the other hand, the iterative implementation will always work but is much less elegant and tougher to conceptualize.
For implementations, the node class and the binary search trees are implemented as:
Recursive Implementations
The recursive implementations intuitively follow from the definitions of the traversal orders. In pre-order, the parent value is pushed before the recursive calls of the left and right children. In in-order, the parent value is pushed between the recursive calls of the left and right children. In post-order, the parent value is pushed after the recursive calls of the left and right children.
Although these implementations are elegant, they don’t work for large trees. This is why iterative implementations are preferred.
Iterative implementations
A stack is used for iterative implementations. Nodes are pushed in and popped off the stack until there are no more nodes in the tree left to traverse.
Pre-order
Preorder traversal is the easiest of the three to implement iteratively, because it is done top-down. Unlike the other two, which are bottom-up, there is no need to verify that the current node does not have any children before pushing to traversed. When the choice between the three traversals is unimportant, this is the preferred implementation because it’s iterative and the most concise.
In the code above, the stack is initialized with the root (line 2). Since nodes are pushed when the the left and right child are not null, the stack will be empty when the tree has been completely traversed (line 6).
More so, the right child is pushed to the stack before the left child. This is to maintain the left child before right child ordering when they are popped off the stack (i.e., pushed right then left so the popped order is left then right).
Note that it is unimportant whether the push to traversed occurs on line 8, 9, or 10. What is important is that the stack is popped first (line 7), right is pushed next (line 8), and left is pushed last (line 9).
Alternatively, the pre-order traversal can be done as shown above as well. This approach mirrors the iterative in-order traversal shown below, with the distinction being when the push to traverse occurs. Here, the push occurs before the assignment of curr to the left and right children (lines 8, 10, and 13).
In-order
In-order is a bottom-up traversal. The while loop pushes to the stack until there are no more left children (lines 7–10). Then, pop off the stack and push to traversed (lines 11–12).
The reassignment of curr to the right child (line 13) and the while loop that precedes it (line 7) make it so that the pushes to traversed (line 12) only occur when curr is pointing to the bottom node that has not been pushed to traversed. Each pop is equivalent to a backtrack.
More so, the push to traversed occurs between the assignment of curr to the left and right children (lines 9, 12, and 13). Intuitively, this follows from the definition of in-order traversal.
Post-order
This two stack implementation of post-order traversal mirrors the first pre-order implementation. The two distinctions are:
1. The left child is pushed to the stack before the right child
2. The push to the second stack occurs after the children are pushed to the first stack.
The second while loop (lines 14–17) serves to populate traversed by reversing the second stack.
Alternative, the second while loop can be avoided by returning the second stack reversed (line 13). Note that these two implementations have the same time complexity.
This can be done with one stack as shown above, but, since the time and space complexities of all three implementations are the same, this implementation should be avoided.
Build applications differently
OSS Tools like Bit offer a new paradigm for building modern apps.
Instead of developing monolithic projects, you first build independent components. Then, you compose your components together to build as many applications as you like. This isn’t just a faster way to build, it’s also much more scalable and helps to standardize development.
It’s fun, give it a try →
Learn more
- Building a React Component Library — The Right Way
- 7 Tools for Faster Frontend Development in 2022
- Microservices are Dead — Long Live Miniservices
Depth-First Search of a Binary Tree in JavaScript was originally published in Bits and Pieces on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Bits and Pieces - Medium and was authored by Yogi Paturu
Yogi Paturu | Sciencx (2022-02-24T13:07:15+00:00) Depth-First Search of a Binary Tree in JavaScript. Retrieved from https://www.scien.cx/2022/02/24/depth-first-search-of-a-binary-tree-in-javascript/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
