This content originally appeared on Level Up Coding - Medium and was authored by Alex Powell
Interviewing at Google is tough. Put your coding and math chops to the test with this fun and challenging question from a past interview.
The Question
Given a graph G, count the number of unique k-step paths from node X to node Y.
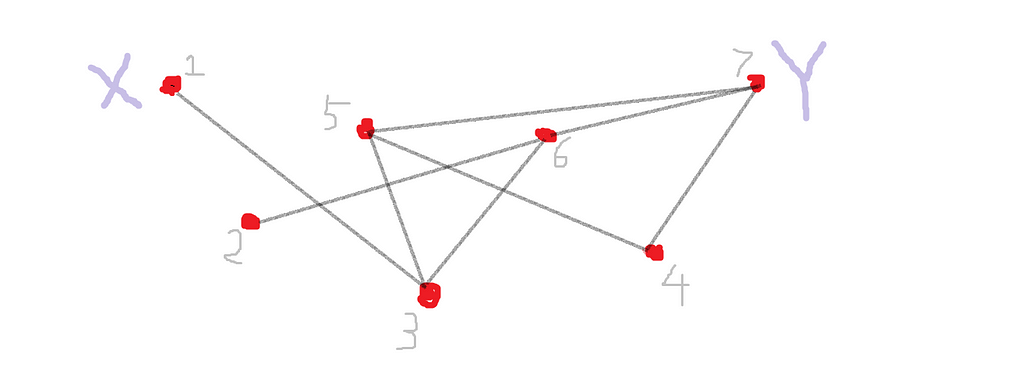
Solution 1
The first step is to construct the adjacency matrix of the graph. The adjacency matrix is a matrix of 1s and 0s that encode the connectivity information of the graph. If an edge exists, the corresponding entry in the graph is 1, otherwise it is 0.
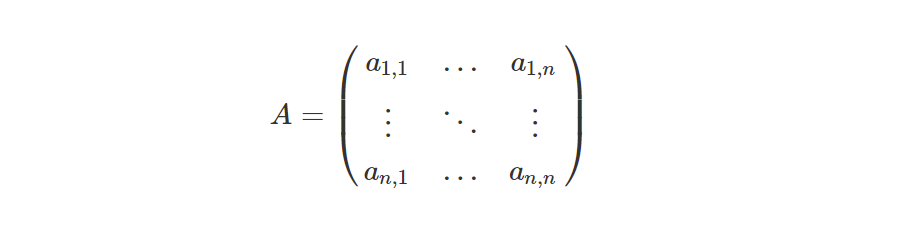
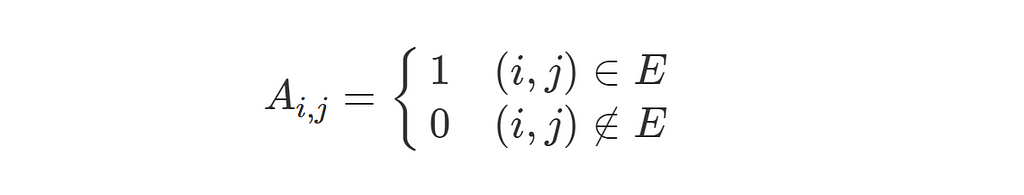
The adjacency matrix for the sample graph G on 7 vertices given above is:
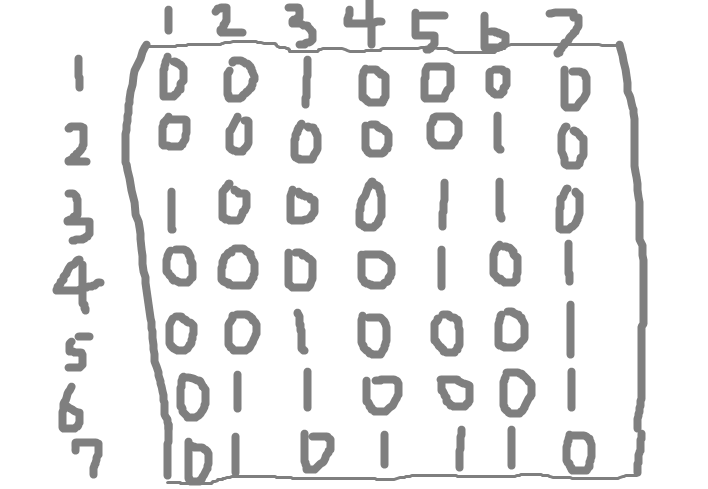
Now for the trick: we can take matrix powers of the adjacency matrix to count the number of distinct paths from any node to any other. If you need a review of matrix multiplication, check out this page.
For k=2 (2-step paths), we can square the matrix and consider entry (i, j).
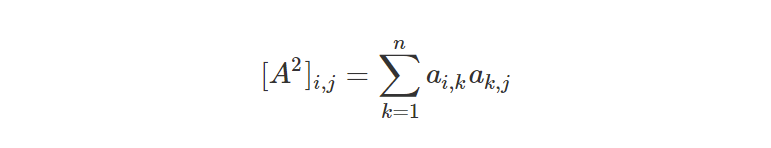
This quantity is exactly what we want, because it counts the number of paths between node i to intermediate node k to node j, where k ranges between all possible intermediate nodes k. If both edges (i, k) and (k, j) exist, then a_ik and a_kj are both equal to 1, which adds 1 to the total sum. If one of the edges doesn’t exist, then the product is zero and the sum is not increased.
The answer to the generic version of this problem is
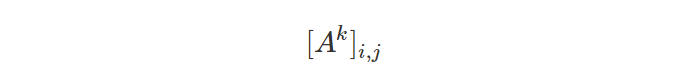
This can be shown using induction.
Time Complexity Analysis
For the k step case, if we natively multiply the matrices one by one (using a for loop for example), then the time complexity is
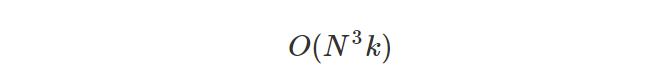
because the time complexity of matrix multiplication is cubic. However, this solution is suboptimal, because when k is large, the operations needed is quite big!
Solution 2 — With Optimization
Instead of naively doing multiplications, we can apply fast exponentiation, which can be seen as dynamic programming, memoization, or recursion. We compute powers of A by recursively taking smaller powers of A. For example, to calculate A¹⁶, we would write A¹⁶ = (A⁸)(A⁸). Then A⁸ = (A⁴)(A⁴). Then A⁴=(A²)(A²). So it turns out we only need to do A², (A²)², (A⁴)² and (A⁸)², which is 4 matrix multiplications and not 15!
The time complexity is
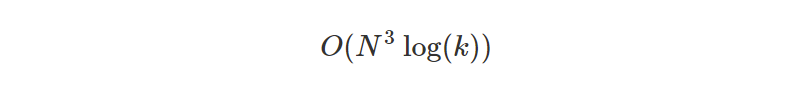
Pretty good!
Solution 3 — Even Faster
The optimal solution is to precompute a special factorization of the matrix A: the singular value decomposition of A. Since A is a symmetric matrix, this corresponds to an orthogonal decomposition
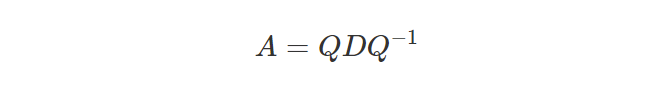
where D is a diagonal matrix and Q is an orthogonal matrix. All of this is to say that the kth power of A is given by
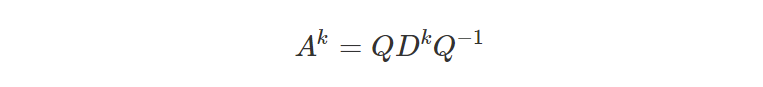
which can be computed quickly because D is diagonal! If we use the fast exponentiation trick to take powers of the diagonal elements of D, we can compute the kth power of D in logarithmic time as well.
Because the time complexity for forming the decomposition is cubic in N, the overall time complexity of this approach is
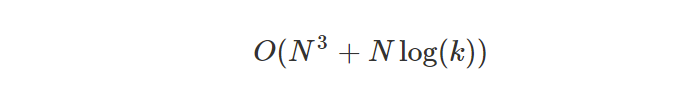
Conclusion
Google as well as other tech companies love to follow up on questions by asking about time complexity (and space complexity). In this question, we got to see lots of time complexity analysis, matrix algebra, and reasoning using the adjacency matrix of a graph.
Level Up Coding
Thanks for being a part of our community! More content in the Level Up Coding publication.
Follow: Twitter, LinkedIn, Newsletter
Level Up is transforming tech recruiting ➡️ Join our talent collective
Solving a Hard Google Interview Question about Path Counting using Matrices was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Alex Powell
Alex Powell | Sciencx (2022-07-11T00:13:49+00:00) Solving a Hard Google Interview Question about Path Counting using Matrices. Retrieved from https://www.scien.cx/2022/07/11/solving-a-hard-google-interview-question-about-path-counting-using-matrices/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
