This content originally appeared on Level Up Coding - Medium and was authored by Roman Kositski
Or how to get from Cape Town to Magadan
How I got into this
A while back I came across a programming challenge posted by one of the big tech companies on Facebook as a way to get people to send CV’s. The challenge was to find the shorted across a 1000x1000 chessboard. Each cell of the board had a number assigned to it. The shortest “path” is the lowest sum of the cell values that make up a consecutive path from one vertices (say top left) to the other end on the far side (bottom right).
All you had to do is to submit the length of the path (as a single number) and have a good chance in winning a new XBox or something like that (I can’t remember the exact prize).
Reading the challenge got me curious. It felt as a simple problem on one hand, and something anyone with very basic coding skills should be able to tackle. But on the other hand I did understand that there is a huge amount of possible paths and a brute force approach won’t cut it.
So I thought about the problem for an hour or so and dropped it. I do hope that the guy or gal that won that XBox is still enjoying it.
Many months had passed and I saw a post that was circulating for a while about the longest path you can walk based on Google Maps. This reminded me that problem I saw in that coding challenge and I’ve decided to get back to it and solve it.
Now get me that XBox please.
Problem definition
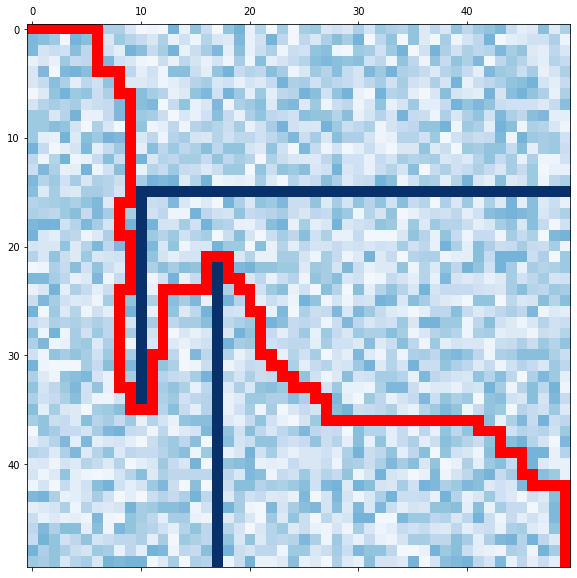
We have a matrix/grid/array with size of X over X (or XxX if I may). Each cell is populated by a number (let’s assume its a positive integer but it can be any number). The start cell and the end cell have values of zero. You start from the upper left corner and need to get to the bottom right. You can move only to adjacent cells either by sliding right, left, up or down (and not leaving the array). The goal is to find the path which makes the sum of values you’ve passed the lowest. An example of such 10x10 grid is shown in the figure below.
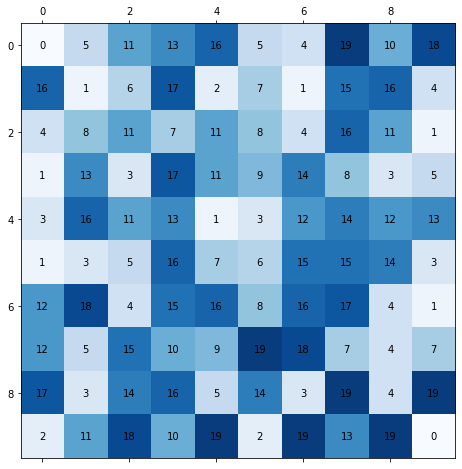
And the Python code to generate that array (I used a random number generator, so you’ll get similar but not exactly the same array):
The solution for that specific grid would be 116 and the path is marked on the following image:
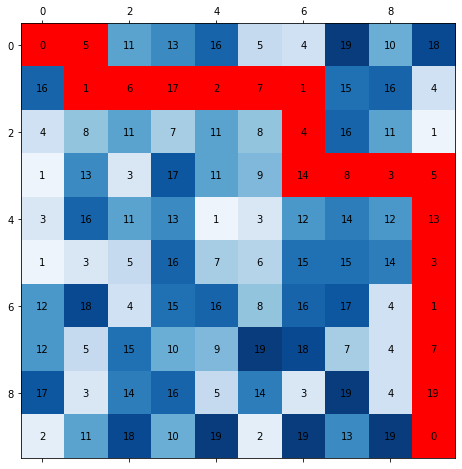
At this point you can stop reading and try to figure out a solution. No, an XBox is not promised, but let me know how you did.
Dijkstra’s algorithm
The problem of finding the shortest path between two nodes in a map (in a general sense) is by far not a new problem. One of the first, and probably best known, path finding algorithms is Dijkstra’s algorithm named after its inventor the Dutch computer scientist Edsger Wybe Dijkstra. There are numerous resources on the internet about this algorithm, but while I was trying to figure it out it was quite hard to find a good reference. The best resource I found was a video made by Computerphile on YouTube. I’ll try my best to explain the basic concepts behind “Dijkstra”. I’ll stick with the matrix problem and not the more classic “connected graph” case so make sure you watch the above-mentioned clip.
Dijkstra in 100 words or less
Let’s assume we are at a given cell on our map/matrix. From here we can go to any adjacent cell as long as it was not visited previously. We check all adjacent cells and place the numbers from these cells by descending value in a “stack”.
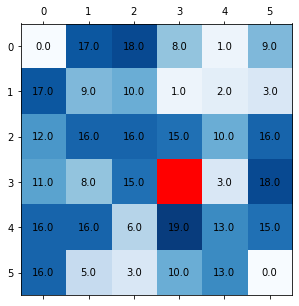
In the case of the matrix on the left, starting from the red cell we order our stack as 3,15,15,19. I will call the step of looking at the cells around as the “explore stage”.
Now we move the the cell which is on the top of the stack. We moved right and stand on the cell with the value of 3. We repeat the explore stage but now we add the values 10,13 and 18 (these are the values around “3”) to the already obtained 3. Now our stack is: 13,15,15,16,19,21 because 3+10, 15, 15, 3+13, 19, 3+18. Now we move again based on the value on the top of our stack to the cell above 3 with the value of 10 (position [2,4]) because it “costs” us just 13 to get there. We will keep this “explore”-”move” once more with a step up [1,4] and again once again up to [0,4]. At this point our path will cost 3+10+2+1=16. But the lowest number in our stack is 15 (look at the above stack). So we will “jump” to the cell with the value of 15 and proceed to do an “explore” stage from there.
The main idea is that we keep that stack of paths and we keep exploring the shortest path until it becomes not the shortest one (at any given “point in time”) so we “jump” to the current shortest path. We keep this exploration until reaching our goal and at that point the algorithm stops.
In every step we make we “remember” the cell that we came from. That way at the end we can backtrack our way until reaching the origin again. For example we will “keep a note” that we moved to [3,4] from [3,3], and to [2,4] from [3,4].
In total we have our original “map” and we also need to keep a matrix of values with the “length” it took us to get to a specific cell. Finally we need to keep an array with the “back step” which tells us from that cell we moved to a specific cell.
Lets code
So the following is a very “non Python” code which was written that way so everything will be as clear as possible.
Let’s break it down
We start by making the “distance map” matrix, the “back track” (originmap) array (we will hold the index of the cell with a single value for simplicity), and a Boolean matrix marking the cells we have visited.
Next we look through the exploration part of the algorithm. We look at the adjacent cell. If the value in the “distance map” is higher then the current path we are on, we will update the distance map. At the end of the exploration iteration we update our position (x,y).
Once we reach our destination we can start back tracking our steps based on the “originmap” array.
And finally we plot again our map and the path we found.
That’s it
I know (from experience) that only by reading this post you won’t understand Dijkstra’s algorithm. The best way to figure it out is to code yourself. That’s how I got it.
Now we can generate interesting maps and find the paths. It’s not the same as waking from Siberia to South Africa, but it’s something.
Dijkstra’s shortest path algorithm in a grid was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Roman Kositski
Roman Kositski | Sciencx (2021-03-07T15:48:24+00:00) Dijkstra’s shortest path algorithm in a grid. Retrieved from https://www.scien.cx/2021/03/07/dijkstras-shortest-path-algorithm-in-a-grid/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
