This content originally appeared on HackerNoon and was authored by Hockey Stick
:::info Author:
(1) Sima Mehri, Farzanegan High School.
:::
Table of Links
Abstract and 1 Introduction and Description of Results
2. Proof of Results and References
2. Proof of Results
In the proof of both theorems, we use induction.
\
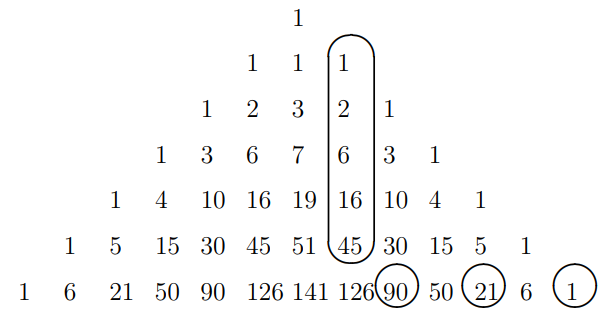
\

\ using properties of Pascal triangle, we get
\
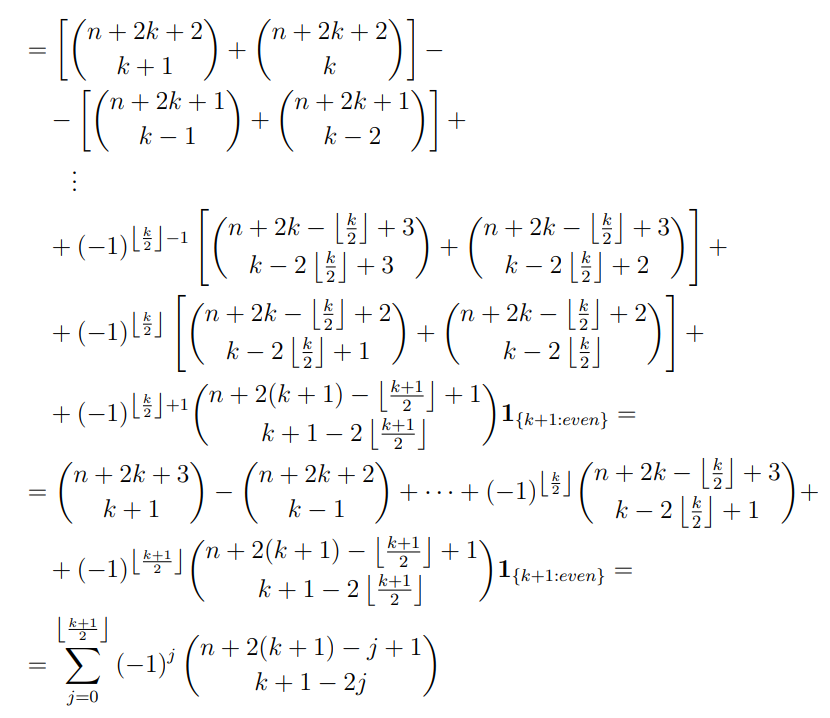
\ The statement for k + 1 is also true, and the proof is completed.
\

\ using properties of the trinomial coefficients, we get
\
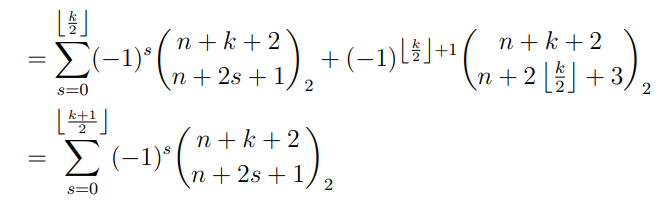
\ The statement for k + 1 is also true, and the proof is completed.
\ The hockey stick theorem in the trinomial triangles has been proved. This theorem can be translated in Pascal pyramid as follows :
\
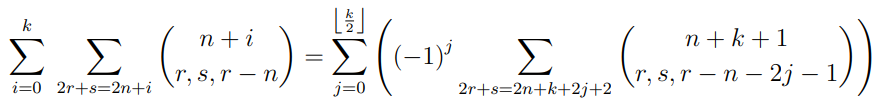
\ Other similar theorems might be obtained for Pascal’s four dimensional and even n-dimensional pyramid.
References
1] G. Andrews, Euler’s ’Exemplum Memorabile Inductionis Fallacis’ and Trinomial Coefficients J. Amer. Math. Soc. 3 (1990), 653-669.
\ [2] P. Hilton and J. Pedersen, Looking into Pascal Triangle, Combinatorics, Arithmetic and Geometry Mathematics Magazine, Vol. 60, No. 5 (Dec., 1987), 305-316.
\ [3] Eric W.Weisstein, Trinomial Coefficient From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/TrinomialTriangle.html
\ [4] Eric W.Weisstein, Trinomial Triangle From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/TrinomialTriangle.html
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Hockey Stick
Hockey Stick | Sciencx (2024-06-26T19:00:14+00:00) Exploring Hockey Stick Theorems: Proof of Results and References. Retrieved from https://www.scien.cx/2024/06/26/exploring-hockey-stick-theorems-proof-of-results-and-references/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
