This content originally appeared on HackerNoon and was authored by Labyrinthine
:::info Authors:
(1) Vinicius Yu Okubo, B.S. in electrical engineering from the University of São Paulo in 2022 and currently, he is pursuing his M.S. in electrical engineering at the University of São Paulo;
(2) Kotaro Shimizu, B.S. degree in Physics from Waseda University, Japan, in 2019 and M.S. degree in Physics from the University of Tokyo, Japan, 2021 and He has been pursuing his Ph.D. in Physics as a JSPS research fellowship for young scientists in the University of Tokyo since 2021;
(3) B.S. Shivaram, received his B.S. degree in Physics, Chemistry and Mathematics from Bangalore University, India, in 1977 and the M.S. degree in Physics from the Indian Institute of Technology, Madras, India, in 1979 and his Ph.D. in experimental condensed matter physics from Northwestern University, Evanston, Illinois in 1984;
(4) Hae Yong Kim, He received the B.S. and M.S. degrees (with distinctions) in computer science and the Ph.D. degree in electrical engineering from the Universidade de São Paulo (USP), Brazil, in 1988, 1992 and 1997, respectively.
:::
Table of Links
III. METHODOLOGY
A. DATASET
In this study, we used films of a ferromagnetic material of recognized technological importance, Bi:YIG, and obtained magnetic images of the labyrinthine patterns using a microscope with polarized light [31]. We specifically focused on the evolution of the labyrinthine patterns under the demagnetization field protocol described below. First, we prepared the sample in the fully saturated state by applying a sufficiently large magnetic field in +z direction, which is perpendicular to the films. In this state, magnetic moments in the Bi:YIG film are forced to point in the field direction. Next, we instantaneously dropped the field to zero and hold it for 10 seconds to get the image. Since the magnetic field is zero, magnetic moments can point upward and downward, resulting in the labyrinthine patterns shown in Fig. 1; the bright and dark regions represent the domains with opposite directions of magnetic moments. Such a process involving switching on and off the magnetic fields is considered half of the demagnetization step. In the remaining half step, a magnetic field was applied with a reduced amplitude and oriented in the opposite direction. We again captured the magnetic domain image after reducing the magnetic field to zero. By repeating these protocols up to 18 steps, we investigated the evolution of the labyrinthine patterns in the demagnetization process step by step. The amplitude of the magnetic field was exponentially reduced with each step. We conducted a series of demagnetization processes from the fully saturated state, repeating this cycle six times. Furthermore, we explored another situation, where the magnetic field was initially applied in the −z direction, and its direction was alternated step by step. Consequently, a total of 12 demagnetization processes were performed, yielding a collection of 444 domain images. All measurements reported here were performed at room temperature. The experimentally obtained images covered an area of 2 mm × 1.8 mm.
\ The original high-resolution color images were converted to grayscale and their resolutions were reduced to 1300×972 to facilitate processing. Furthermore, a median filter with kernel size 3 was applied to reduce noise.
B. TM-CNN OVERVIEW
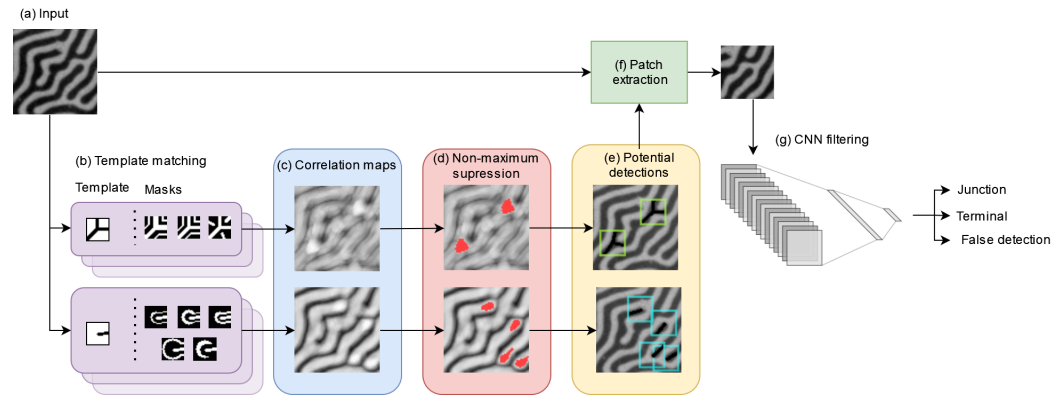
Our approach to detect junctions and terminals in magnetic labyrinthine patterns consists of two sequential steps: proposal of potential detections and their classification between junction, terminal and false detections. It is inspired by other cascaded object detection techniques like Viola and Jones face detection [8], R-CNN [12], and scale and rotation invariant template matching [32].
\ Fig. 3 illustrates the overall structure of TM-CNN. In the first phase, the algorithm generates a preliminary set of potential detections. It must propose all true defects, even if it also generates many false positives. We achieve this by applying template matching detection with a low threshold, followed by a non-maximum suppression. In the second phase, in order to eliminate the false positives, each potential detection is filtered by a CNN classifier.
C. TEMPLATE MATCHING
The basic form of template matching finds instances of a smaller template T within a larger image I. This is done by calculating some similarity metric between the model T and the content of a moving window located at each possible position of I. We measured the similarity between the image and the template using the Normalized Cross Correlation (NCC). NCC is invariant to linear changes in brightness and/or contrast. NCC between template T and image I at pixel (x, y) is calculated as:
\

\ This basic approach is not well suited for detecting junctions and terminals in the magnetic labyrinthine structures because a single template is not capable of modeling:
\
All possible rotations;
\
All deformed shapes of defects.
\ To solve problem (1), we employ a rotation-invariant template matching based on exhaustive evaluation of rotated templates. There are some alternative rotation-invariant techniques based on circular and radial projections [32], [34], and
\
\ on Fourier coefficients of circular and radial projections [35]. These techniques can reduce computational requirements, but their implementations are complex and require parameter tuning. Furthermore, our application does not require exceptional computational performance, as the processing is offline. Thus, our technique uses the standard OpenCV[1] template matching implementation, which is highly optimized using FFT and special processor instructions.
\

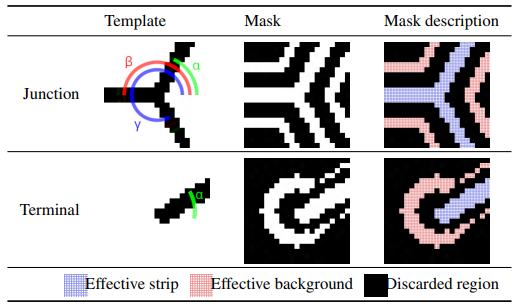
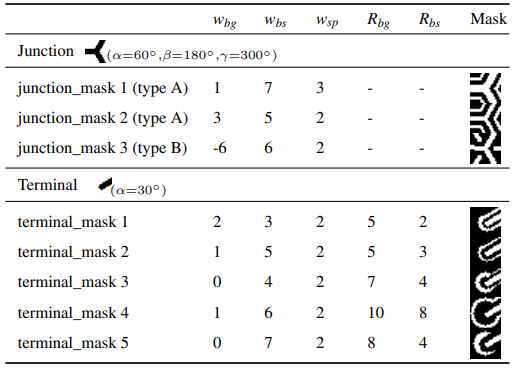
D. TEMPLATES AND MASKS USED IN THE EXPERIMENT
We manually designed templates and masks, and empirically tuned them to capture various junction and terminal shapes. They have 21×21 resolutions and are generated at runtime. Templates represent magnetic strips as black lines radiating from their center drawn on a white background. Meanwhile, masks are created from black backgrounds with white areas defining relevant coordinates used in template matching. Their main purpose is to obscure the space between strips and background, addressing variations in widths and curvatures, and to limit the background regions to reduce interference from neighboring strips. Table 1 exemplifies the templates and masks used to detect junctions and terminals.
\

\ Template matching is applied separately for each (template, mask) pair. Several template matchings are computed in
\
\
\ parallel using the OpenMP library[2]. This process takes about 80 seconds to process an image on an i7-9750H processor.
\ To obtain the final correlation map corr, we calculate the maximum value among all n = 3 × 439 + 5 × 120 = 1917 NCC maps for each position (x, y), that is:
\
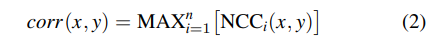
\ Pixels where corr(x, y) exceeds a predefined threshold t are considered potential detections.
\ However, a single junction/terminal may encompass multiple neighboring points with correlation values greater than the threshold t. Therefore, it is necessary to perform some form of non-maximum suppression to eliminate duplicate detections and select only the true center of junction/terminal. Kim et al. [18] present a solution to this problem: Whenever two potential detection points p1 and p2 are separated by a distance smaller than a threshold c, the point with the lowest correlation value is discarded. In this work, we use a slightly different approach, but with the same practical result: Whenever the algorithm finds a potential detection, it executes a breadth-first search algorithm. This algorithm recursively searches adjacent pixels (x, y) where the correlation exceeds 80% of the threshold (that is, corr(x, y) > 0.8t) and saves the pixel with the highest correlation. Subsequently, the searched area has its correlation value set to zero to avoid re-detection. Fig. 3d highlights the searched area in red. The pixel with the highest correlation is chosen as the center of the junction/termination. This process performs detection in a single pass.
E. DATASET ANNOTATION
To classify potential detections into true or false using a CNN classifier, we must first create annotated training images. TM-CNN makes it easier to create training examples, as it allows one to annotate the examples semi-automatically. This process is divided in two phases.
\ 1) Template matching-assisted annotation
\ In this phase, only a small set of images are annotated. Initially, we apply template matching followed by nonmaximum suppression to identify the centers of possible detections, together with their probable labels (junction or terminal). Without this help from template matching, we would have to manually and precisely locate the centers of thousands of defects. Subsequently, a human reviewer makes corrections to ensure that the labels given by the template matching are correct. The reviewer may change the labels to junction, terminal or false detection. After all positive detections are annotated along with a small set of false detections, a larger set of false detections is created by lowering the template matching threshold and sampling new false detections. These images, now with positive and negative annotations, are used to train a preliminary version of the CNN classifier.
\ 2) Deep learning-assisted annotation
\ Due to the small number of images in the initial training set, the preliminary CNN classifier cannot accurately classify all magnetic stripe defects. Nonetheless, this preliminary model is integrated into the annotation procedure to alleviate the required workload. In the second phase, we continue using template matching to generate the initial set of detections. However, the preliminary CNN classifier is employed to identify most of the template matching errors, thus speeding up the annotation process. As new images are annotated, more accurate models are trained to further simplify the annotation workload. The final training set consists of 17 images derived from a single annealing protocol, selected to cover varied experimental configurations of ascending and descending magnetic fields at different magnitudes. Out of these, 16 were selected from the quenched (unordered) state, as they represent a more diverse set of shapes and represent a greater challenge for classification. The training set encompasses a total of 33,772 detections, which includes 12,144 junctions, 12,777 terminals, and 8,851 false detections.
F. CANDIDATE FILTERING BY CNN
Our algorithm extracts small 50×50 patches centered around each detection point and a CNN classifies them into three classes: junction, terminal or false positive. The size of patches for CNN classification is larger than the size of template matching models (21×21), allowing CNN to use more contextual information than template matching.
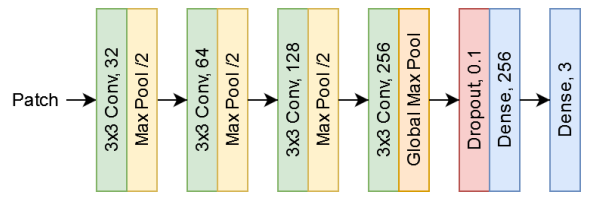
\ We use a simple CNN model to classify the small patches (Fig. 4). It has four convolutional layers with 32, 64, 128 and 256 filters, all using 3×3 kernels. The first three convolutional layers are followed by max pooling layers to downsample the feature maps and global max pooling is applied after the last convolutional layer. This is followed by dropout and two fully connected layers: the first with 128 nodes and the second with three output nodes. The ReLU activation function is used across the model, except at the output layer where the softmax is used. In total, this network has only 422,608 parameters. For comparison, VGG-16 and ResNet-50 (common backbones for detection) have 138 million and 23 million parameters, respectively. Thanks to its simplicity, our model is fast and can make predictions even without GPUs and takes around 30 seconds for filtering each image using an i7-9750H processor with 16 GB of RAM.
\
\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[1] Open Source Computer Vision Library, https://opencv.org
\ [2] Open Multi-Processing, https://www.openmp.org/
\ [3] https://www.tensorflow.org/
This content originally appeared on HackerNoon and was authored by Labyrinthine
Labyrinthine | Sciencx (2024-09-18T15:00:23+00:00) Efficient Detection of Defects in Magnetic Labyrinthine Patterns: Methodology. Retrieved from https://www.scien.cx/2024/09/18/efficient-detection-of-defects-in-magnetic-labyrinthine-patterns-methodology/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
