This content originally appeared on DEV Community and was authored by Aya Bouchiha
Hi, I'm Aya Bouchiha, in this beautiful day, I'm going to explain the Heap data structure.
#day_22
Definition of Heap
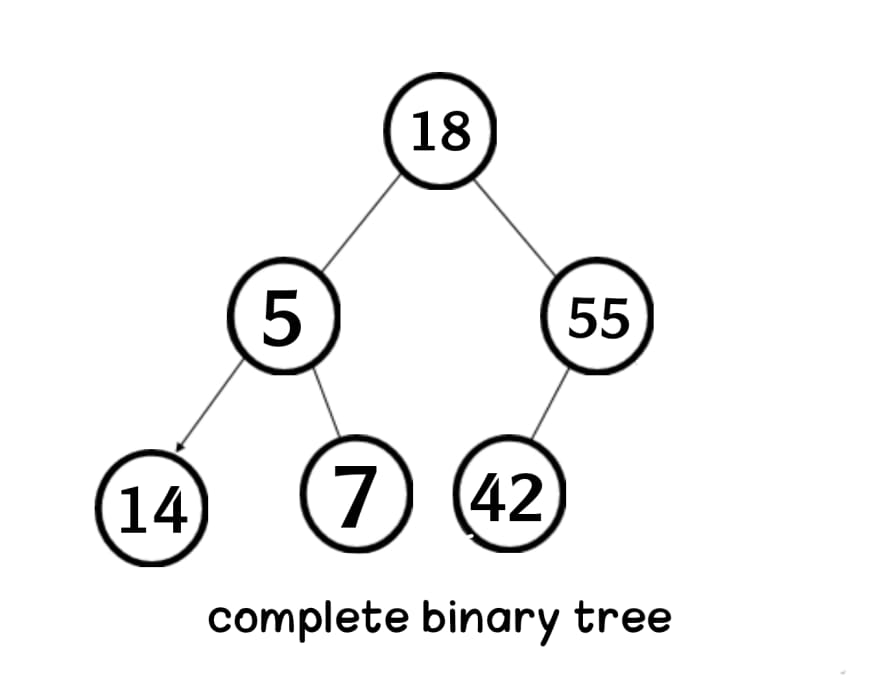
Heap: is a complete binary tree (types of a binary tree) (which each node has at most two children and All the leaves should lean towards the left) where the root node is compared with its children and arrange accordingly.
Example of complete binary tree
Example of incomplete binary tree
Types of Heap
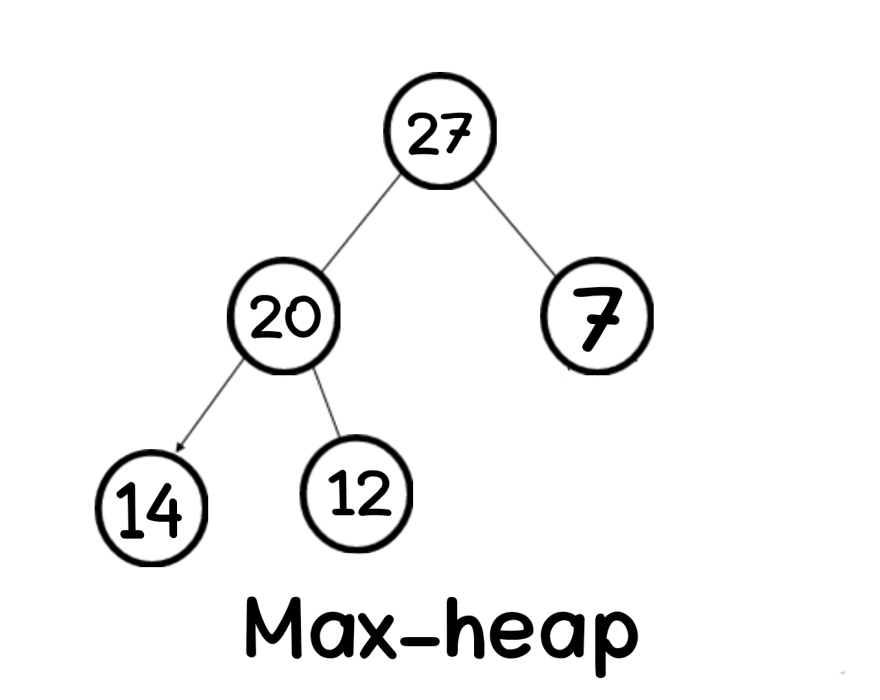
1. Max-heap
The key of every node is smaller than or equal its parent
arr[parent] >= arr[i]
Example of max-heap
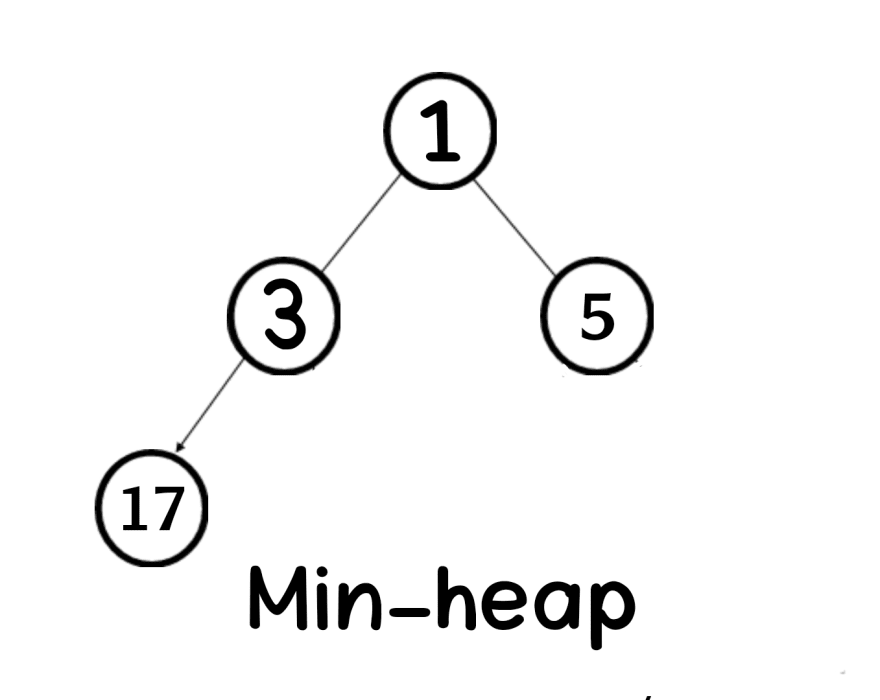
2. Min-heap
The key of every node is greater than or equal its parent
arr[parent] <= arr[i]
Example of min-heap
Application of Heap
- Heap sort algorithm
- Order statistics Getting The minimum value or the maximum value in a constant time
- Graph algorithms like Prim's Algorithm and Dijkstra's algorithm
- Priority Queue
Space and Time complexity of Heap
The space complexity of the heap is O(n)
| insertion (push) | deletion (pop) | peek |
|---|---|---|
| O(log n) | O(log n) | O(1) |
Heap array implementation
let's take this example of max-heap:
the index of each node is between parentheses ( ):
15(0)
/ \
(1) 9 13 (2)
/ \ /
(3)5 (4)7 (5)11
arr = [15, 9, 13, 5, 7, 11]
the implementation can be done by:
- making the root the first element in the array
arr[0] = root - Parent node:
arr[(i - 1) // 2] - Left-child:
arr[2 * i + 1] - Right-child:
arr[2 * i + 2]
class MinHeap:
def __init__(self):
self.heap = []
self.heap_size = 0
def getParentNodeIndex(self, i: int) -> int:
return (i-1)//2
def getLeftChildNodeIndex(self, i: int) -> int:
return 2*i+1
def getRightChildNodeIndex(self, i: int) -> int:
return 2*i+2
def hasParent(self, i: int) -> bool:
# cheking if a node has a parent
return self.getParentNodeIndex(i) < len(self.heap)
def hasLeftChild(self, i: int) -> bool:
# cheking if a node has a left child
return self.getLeftChildNodeIndex(i) < len(self.heap)
def hasRightChild(self, i: int) -> bool:
# cheking if a node has a right child
return self.getRightChildNodeIndex(i) < len(self.heap)
def getMinValue(self) -> int:
"""
time complexity => O(1)
"""
return self.heap[0]
def printAll(self):
print(self.heap)
Insertion (push) in Heap
1. Approach of insertion
- Increase the size of the heap to add a new element
- The heap is a complete binary tree that's why the new element should lean towards the left, which means, in array representation, we insert the element at the end of the array.
- Heap must satisfy the heap-order property, that's why we should Heapify or bubble up the new element, Heapify or bubbling up is swapping the new element with its parent until
- its parent is greater than or equal to it in a max-heap.
- its parent is smaller than or equal to it in min-heap.
1. Explanation of insertion
For better understanding, let's take an example:
we want to insert 1 in this min-heap
3 (0)
/ \
(1) 5 10 (2)
/
9 (3)
[3, 5, 10, 9]
- Insert the new Element at the end of the array
3 (0)
/ \
(1) 5 10 (2)
/ \
(3)9 (4)1
heap_size += 1
arr = [3, 5, 10, 9, 1]
- Bubble up the new element
- Since 1 < 5, swap them, so:
3 (0)
/ \
(1) 1 10 (2)
/ \
(3)9 (4)5
arr = [3, 5, 10, 9, 1]
newElementIndex = len(arr) - 1 # 4
# the index of the parent of the new element
ParentIndex = (newElementIndex - 1) // 2 # (4-1)//2 = 1
# 1 < 5
if arr[newElementIdx] < arr[ParentIdx]:
# swap(1, 5)
arr[newElementIdx], arr[ParentIdx] = arr[ParentIdx], arr[newElementIdx]
the array will be:
arr = [3, 1, 10, 9, 5]
- Hence 1 < 3, swap them, so:
1 (0)
/ \
(1) 3 10 (2)
/ \
(3)9 (4)5
we'll do the same process for 1 and 3 like (1 and 5) so the array will be
arr = [1, 3, 10, 9, 5]
3. Implementation of insertion in python
the implementation of bubble up or heapify function in python
def bubbleUp(self, i: int):
parentIndex = self.getParentNodeIndex(i)
if parentIndex < 0:
parentIndex = 0
# Loops until it reaches a leaf node
while(i > 0 and self.heap[i] < self.heap[self.getParentNodeIndex(i)]):
# Swap the elements
self.heap[i], self.heap[self.getParentNodeIndex(i)] = self.heap[self.getParentNodeIndex(i)], self.heap[i]
i = self.getParentNodeIndex(i)
the implementation of insert function in python
def insert(self, value: int):
self.heap_size += 1
# insert the element at the end
self.heap.append(value)
# bubble up the new element
self.bubbleUp(len(self.heap) - 1)
Deletion in Heap
1. Approach of Deletion
The standard deletion operation on Heap is deleting the root which is the maximum value of the max-heap, and the minimum value of the in-heap.
- Decrease the size of the heap to delete the element
- Swap the root with the last element
- Pop (delete) last element of the array
- Heap must satisfy the heap-order property, that's why we should bubble-down (also known as heapify, percolate-down, sift-down, sink-down, trickle-down, heapify-down, cascade-down, extract-min or extract-max, or down-heap) the new element, bubble-down is swapping the new element with one of its children until
- the child is smaller than or equal to it in a max-heap.
- the child is greater than or equal to it in a min-heap.
1. Explanation of deletion
For better understanding, let's take an example:
we want to delete 3 in this min-heap
3 (0)
/ \
(1) 5 10 (2)
/
9 (3)
[3, 5, 10, 9]
- Swap the root with the last element
9 (0)
/ \
(1) 5 10 (2)
/
(3)3
arr = [9, 5, 10, 3]
- Delete the last element and decrease the size of the array
9 (0)
/ \
(1) 5 10 (2)
arr = [9, 5, 10, 3]
heap_size -= 1
arr.pop()
so the array will be
arr = [9, 5, 10]
- Bubble down the root
- Since 9 > 5, swap them, so:
5 (0)
/ \
(1) 9 10 (2)
arr = [5, 9, 10]
3. Implementation of deletion in python
Bubble down implementation in python
def bubbleDown(self):
# the index of the root => 0
i = 0
while True:
smallest = None
leftChildIndex = self.getLeftChildNodeIndex(i)
rightChildIndex = self.getRightChildNodeIndex(i)
# if the node has not any child
if (not self.hasLeftChild(i) and not self.hasRightChild(i)):
break
# if the node has only a left child
elif (not self.hasRightChild(i)):
# the smallest variable will be the index of the left child
smallest = leftChildIndex
# if the node has only a right child
elif (not self.hasLeftChild(i)):
# the smallest variable will be the index of the right child
smallest = rightChildIndex
# if the node has 2 children
else:
# the smallest variable will be the smallest value of the 2 children
smallest = rightChildIndex if self.heap[rightChildIndex] < self.heap[leftChildIndex] else leftChildIndex
# if the node's value is greater than its one of children
if (self.heap[i] > self.heap[smallest]):
# swap the node with its child
self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
# the i variable will be the index of the smallest value of the two children
i = smallest
# if the node's value is smaller than its one of children
else:
break
return
delete implementation in python
def delete(self):
# if the size the heap is one or the heap is empty(size = 0)
if self.heap_size <= 1:
self.heap = []
return
# replace last element with the root
self.heap[self.heap_size - 1], self.heap[0] = self.heap[0], self.heap[self.heap_size - 1]
# decrease the size of heap
self.heap_size -= 1
# delete last element
self.heap.pop()
self.bubbleDown()
Heap implementation in python (Final code)
class MinHeap:
def __init__(self):
self.heap = []
self.heap_size = 0
def getParentNodeIndex(self, i: int) -> int:
return (i-1)//2
def getLeftChildNodeIndex(self, i: int) -> int:
return 2*i+1
def getRightChildNodeIndex(self, i: int) -> int:
return 2*i+2
def hasParent(self, i: int) -> bool:
# cheking if a node has a parent
return self.getParentNodeIndex(i) < len(self.heap)
def hasLeftChild(self, i: int) -> bool:
# cheking if a node has a left child
return self.getLeftChildNodeIndex(i) < len(self.heap)
def hasRightChild(self, i: int) -> bool:
# cheking if a node has a right child
return self.getRightChildNodeIndex(i) < len(self.heap)
def getMinValue(self) -> int:
"""
time complexity => O(1)
"""
return self.heap[0]
def insert(self, value: int):
self.heap_size += 1
# insert the element at the end
self.heap.append(value)
# bubble up the new element
self.bubbleUp(len(self.heap) - 1)
def bubbleUp(self, i: int):
parentIndex = self.getParentNodeIndex(i)
if parentIndex < 0:
parentIndex = 0
# Loops until it reaches a leaf node
while(i > 0 and self.heap[i] < self.heap[self.getParentNodeIndex(i)]):
# Swap the elements
self.heap[i], self.heap[self.getParentNodeIndex(i)] = self.heap[self.getParentNodeIndex(i)], self.heap[i]
i = self.getParentNodeIndex(i)
def delete(self):
# if the size the heap is one or the heap is empty(size = 0)
if self.heap_size <= 1:
self.heap = []
return
# replace last element with the root
self.heap[self.heap_size - 1], self.heap[0] = self.heap[0], self.heap[self.heap_size - 1]
# decrease the size of heap
self.heap_size -= 1
# delete last element
self.heap.pop()
self.bubbleDown()
def bubbleDown(self):
# the index of the root => 0
i = 0
while True:
smallest = None
leftChildIndex = self.getLeftChildNodeIndex(i)
rightChildIndex = self.getRightChildNodeIndex(i)
# if the node has not any child
if (not self.hasLeftChild(i) and not self.hasRightChild(i)):
break
# if the node has only a left child
elif (not self.hasRightChild(i)):
# the smallest variable will be the index of the left child
smallest = leftChildIndex
# if the node has only a right child
elif (not self.hasLeftChild(i)):
# the smallest variable will be the index of the right child
smallest = rightChildIndex
# if the node has 2 children
else:
# the smallest variable will be the smallest value of the 2 children
smallest = rightChildIndex if self.heap[rightChildIndex] < self.heap[leftChildIndex] else leftChildIndex
# if the node's value is greater than its one of children
if (self.heap[i] > self.heap[smallest]):
# swap the node with its child
self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
# the i variable will be the index of the smallest value of the two children
i = smallest
# if the node's value is smaller than its one of children
else:
break
return
def printAll(self):
print(self.heap)
my_heap = MinHeap()
my_heap.insert(5)
my_heap.insert(10)
my_heap.insert(1)
my_heap.insert(2)
my_heap.insert(3)
my_heap.insert(4)
# 1
# / \
# 2 4
# / \ /
# 10 3 5
my_heap.printAll()
my_heap.delete()
my_heap.printAll()
# 2
# / \
# 3 4
# / \
# 10 5
print(my_heap.heap_size) # 5
print(my_heap.getMinValue()) # 2
References and useful resources
- https://www.geeksforgeeks.org/array-representation-of-binary-heap/
- https://blog.devgenius.io/how-to-implement-a-binary-heap-javascript-d3a0c54112fa
- https://www.section.io/engineering-education/heap-data-structure-python/
- https://en.wikipedia.org/wiki/Heap_(data_structure)#:~:text=In%20computer%20science%2C%20a%20heap,to%20the%20key%20of%20C.
- https://www.youtube.com/watch?v=dM_JHpfFITs
- https://www.youtube.com/watch?v=NEtwJASLU8Q
if you have any suggestions for the next posts or any questions you can contact me in telegram
Happy coding :)
#day_22
This content originally appeared on DEV Community and was authored by Aya Bouchiha
Aya Bouchiha | Sciencx (2021-07-05T00:38:08+00:00) Your complete guide to Heap data structure!. Retrieved from https://www.scien.cx/2021/07/05/your-complete-guide-to-heap-data-structure/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.