This content originally appeared on Level Up Coding - Medium and was authored by Jessica Trinh
Kadane’s Algorithm — Solving for Maximum Subarray in O(n) Time and O(1) Space

Introduction
Kadane’s Algorithm is able to find the maximum sum of a contiguous subarray in an array with a runtime of O(n). This algorithm is known for being able to elegantly solve the maximum subarray problem and its variations (see it here on LeetCode).
You may come across the maximum subarray problem in industry if your work encounters genomic sequence analysis and computer vision.
The Gist
Kadane’s Algorithm finds the maximum value that can be generated from a subarray for all the subarrays ending at each index.

For instance, in this example, the blue brackets [] indicate a subarray that is being evaluated.
The first row is the original given array. The second row is the first subarray holding only a value of -2. The third row is another subarray holding the values -2 and 1.
This sequence would continue until we reach the end of the array at value 4, index 8, where we would ideally have found the solution to our problem.
Logical Outline
As we get to a new index while still trying to find the maximum sum ending at that same index, we have two options to consider to achieve our goal:
- Take the maximum sum that was ending at the previous index and add the current number (current_max_sum + num)
- Or only use the current number (num)

Working off of the example above: [-2, 1, -3], 4, -1, 2, 1, -5, 4]
The current_max_sum is -4 (derived from -2 + 1 + -3) and the num at the next index is 4. If we go with option 1, the new maximum sum will be 0 (-4 + 4); because of that it is not worth adding to the current number, therefore we’ll choose the second option and move forward with the current number(4).
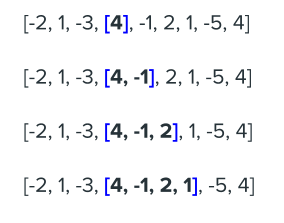
Future iterations continue as discussed to ultimately find that subarray [4, -1, 2, 1] has the largest sum of 6.
So far we are tracking the current_max_sum based on the end of a subarray. But ultimately, what we are trying to accomplish is finding the maximum sum from a subarray.

Continuing off of the same example: [-2, 1, -3, [4, -1, 2, 1], -5, 4]
In this iteration final_max_sum is 6, (4 + -1 + 2 + 1) and at the previous index (4 + -1 + 2) current_max_sum was 5. Since 6 is larger than 5, the final_max_sum value was updated to 6 in the latest iteration.
Code
Like all algorithms, Kadane’s Algorithm is language agnostic but here is an example implementation in Python3 which combines the two formulas discussed above.
Happy coding(:
Kadane’s Algorithm — Solving for Maximum Subarray in O(n) Time and O(1) Space was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Jessica Trinh
Jessica Trinh | Sciencx (2021-09-04T02:24:05+00:00) Kadane’s Algorithm — Solving for Maximum Subarray in O(n) Time and O(1) Space. Retrieved from https://www.scien.cx/2021/09/04/kadanes-algorithm%e2%80%8a-%e2%80%8asolving-for-maximum-subarray-in-on-time-and-o1-space/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
