This content originally appeared on Level Up Coding - Medium and was authored by Prateek Chhikara
This article will illustrate how much money one should pay for insurance to avoid certain risks.

This article is a continuation of my previous article on “Decision Theory: Expected Utility and Risk Aversion”. Make sure to check it out to have some insights required for this article.
Decision Theory: Expected Utility and Risk Aversion
Risk Aversion
The term risk-averse describes the person who may prefer a certain outcome (with 100% probability) with a lower pay-off over an uncertain outcome with a higher pay-off. In simpler terms, the extent to which individuals are willing to bear risks is known as Risk Aversion. Most people are risk averts, and therefore they buy insurance to avoid risk. Low-risk means stability; a low-risk investment assures a reasonable return, with a near-zero chance that any existing investment will be lost. Usually, the return on a low-risk investment will match, or slightly exceed, the level of inflation over time; however, a high-risk investment may gain or lose loads of money.
“If you don’t take risk, you cannot create a future.” — Monkey D Luffy
Properties of a Utility Function for Risk Aversion
If we have a risk-averse problem, the utility function has the following properties.
- It should be monotonically increasing, i.e., the first-order derivative should be positive.
- It should be concave, i.e., the second-order derivative should be negative.
- It should obey diminishing marginal utility of money. For instance, if a person is poor, $10 will give the person a high marginal utility as the person can buy meals for a day with that $10. However, for a billionaire this extra $10 will not provide with some additional marginal utility.
Now, we have to find how much money or premium a risk-averse person will pay to the insurance corporation to avoid risk and uncertainty facing him.
Note: Just for the explanation purpose, we are using √x as the utility function for risk aversion as it satisfies all the above three properties.
Let us take a scenario, suppose I have a house that provides me with a yearly income of $50,000. In the case of an earthquake (the probability of an earthquake is half), due to the damage, my yearly income could be reduced to $10,000. My income with probabilites can be written as follows.
(1/2 ; $50000 | 1/2 ; $10000)
The expected value (EV) of income in this risky and uncertain situation is.
EV = 1/2 * ($50000) + 1/2 * ($10000)
EV = $30000
The expected income of $30,000 is the weighted average of the two uncertain alternatives using their probabilities, and therefore, the expected income is not the actual income that I would get.
We can calculate the expected utility (EU) using the weighted average of individual utilities as shown below.
EU = 1/2 * (utility of $50000) + 1/2 * (utility of $10000)
EU = 1/2 * (√50000) + 1/2 * (√10000)
EU = 161.8
Now, we will find out the amount for certain which will provide me a utility value of 161.8.
√x = 161.8 => x ~ $26180
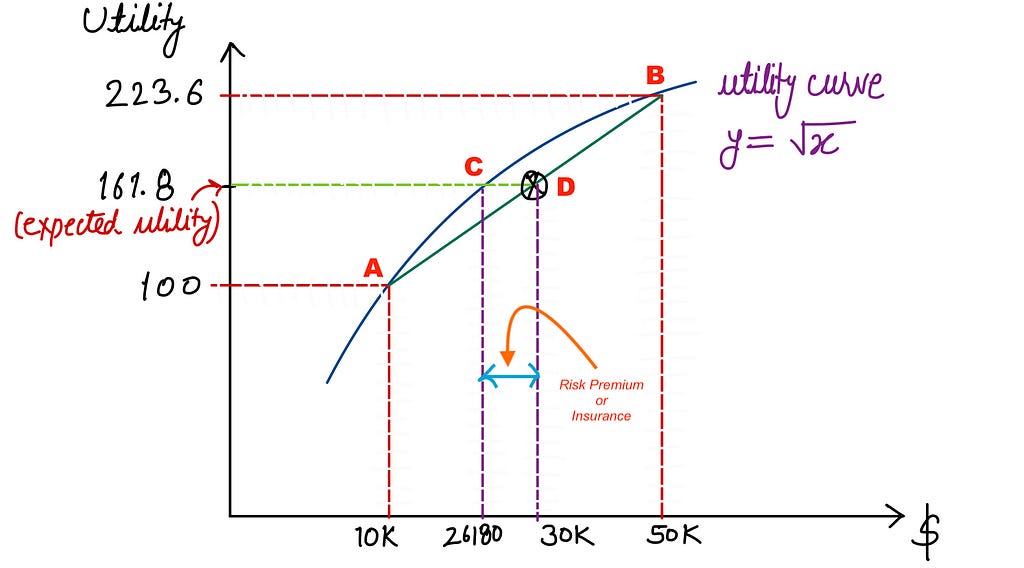
Figure 1 shows the utility curve and the expected utility value for our example. The utility for playing the lottery/gamble is $26,180. This means that I should have at least $26,180 left to make me indifferent to any damage to my house. In other words, I am not going to pay for insurance if I am left with money less than $26,180. The maximum amount of money that the insurance company can charge me is $23,820 ($50,000 — $26,180). If the company charges me more than $23,820, I will have less amount left in hand, so I will be at a disadvantage for taking the insurance. In that case, I would prefer to play the gamble because I can have at least $26180 of utility.
We can understand it in another way. If I give up $3820 ($30000 — $26180) from my uncertain expected income, I will get the same utility of 161.8 as a certain income of $26,180. The $3820 (equal to distance CD in Figure 1) is also called a risk premium.
Conclusion
This article demonstrated how to calculate the maximum money that one should pay for the insurance to avoid a specific risk through an example.
References
Risk Aversion: When Should You Buy Insurance? was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Prateek Chhikara
Prateek Chhikara | Sciencx (2022-02-27T20:19:41+00:00) Risk Aversion: When Should You Buy Insurance?. Retrieved from https://www.scien.cx/2022/02/27/risk-aversion-when-should-you-buy-insurance/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
