This content originally appeared on Level Up Coding - Medium and was authored by Mazin Awad

Finite State Machines (FSMs) are a powerful tool for modeling and controlling systems that have a limited number of states and inputs. In software development, FSMs are commonly used to design user interfaces, create game mechanics, build chatbots, and implement various communication protocols. They can be implemented in different ways, ranging from simple switch-cases to more complex object-oriented solutions such as the state pattern.
In this article, we will explore the implementation of an FSM to simulate the behavior of an ant searching for a leaf, avoiding danger, and returning home with the leaf. We drew inspiration from this excellent tutorial by Fernando Bevilacqua and will create our own version using transition tables.
So, What’s a Transition Table?
A transition table can be viewed as a chart that shows how a Finite State Machine (FSM) works. It lists the states of the FSM and the inputs or conditions needed for it to move between those states. Each cell in the table indicates the next state the FSM will go to based on the current state and the input or condition applied. Let’s see how we can use a transition table to reimplement the Ant brain FSM from the tutorial.
An Ant Brain FSM: States and Transactions
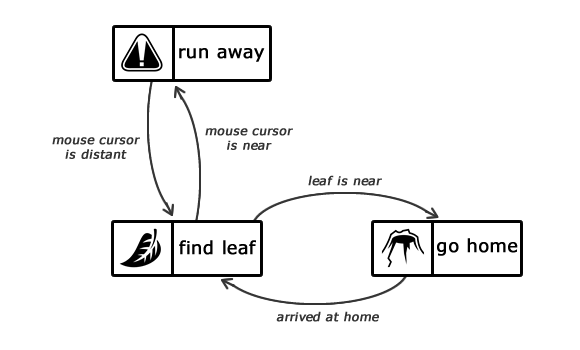
An FSM can only exist in a single state at any given time, and it requires input to transition from one state to another. This input can come from either an external event or the current state of the FSM itself. The diagram presented above displays the various states of the Ant brain FSM and the events needed to trigger a transition from one state to the next. If we assume that the FSM starts in the find leaf state, it requires the event leaf is near to transition to the go home state.
We will first implement the FSM using switch-case method and then refactor the code to use a transition table.
// Ant Brain FSM using the traditional switch-case method
enum
{
NO_CHANGE = 0xff,
};
enum ExternalEvent_e
{
MOUSE_CURSOR_NEAR = 0,
MOUSE_CURSOR_DISTANT,
LEAF_NEAR,
ARRIVED_HOME,
EVENT_COUNT,
};
enum AntBrainStateCode_e
{
FIND_LEAF = 0,
RUN_AWAY,
GO_HOME,
STATE_COUNT,
};
struct AntBrainState_t
{
enum AntBrainStateCode_e code;
void (*stateFn)(void);
};
// State functions
void ant_brain_find_leaf(void);
void ant_brain_run_away(void);
void ant_brain_go_home(void);
enum ExternalEvent_e get_current_event(void);
void ant_brain_run(void)
{
struct AntBrainState_t find_leaf_state = {
.code = FIND_LEAF,
.stateFn = &ant_brain_find_leaf,
};
struct AntBrainState_t run_away_state = {
.code = RUN_AWAY,
.stateFn = &ant_brain_run_away,
};
struct AntBrainState_t go_home_state = {
.code = GO_HOME,
.stateFn = &ant_brain_go_home,
};
struct AntBrainState_t current_state = find_leaf_state;
for (;;)
{
current_state.state_fn();
enum AntBrainEvent_e some_external_event = get_current_event();
struct AntBrainState_t next_state = {.code = NO_CHANGE};
switch (current_state.code)
{
case FIND_LEAF:
if (some_external_event == MOUSE_CURSOR_NEAR)
{
next_state = run_away_state;
}
else if (some_external_event == LEAF_NEAR)
{
next_state = go_home_state;
}
break;
case RUN_AWAY:
if (some_external_event == MOUSE_CURSOR_DISTANT)
{
next_state = find_leaf_state;
}
break;
case GO_HOME:
if (some_external_event == ARRIVED_HOME)
{
next_state = find_leaf_state;
}
break;
default:
break;
}
if (next_state.code != NO_CHANGE)
{
current_state = next_state;
}
}
}
As you may have noticed, the switch-case method can quickly lead to cluttered and hard-to-maintain code, particularly as the number of states and transitions increases. This can make it challenging to update or modify the FSM, making it less flexible and adaptable to changes.
Now let’s refactor the code to use a transition table instead.
// Ant Brain FSM using a Transition Table
...
void ant_brain_run(void)
{
struct AntBrainState_t find_leaf_state = {
.code = FIND_LEAF,
.stateFn = &ant_brain_find_leaf,
};
struct AntBrainState_t run_away_state = {
.code = RUN_AWAY,
.stateFn = &ant_brain_run_away,
};
struct AntBrainState_t go_home_state = {
.code = GO_HOME,
.stateFn = &ant_brain_go_home,
};
struct AntBrainState_t no_change = {.code = NO_CHANGE};
struct AntBrainState_t transition_table[STATE_COUNT][EVENT_COUNT] = {
{ // FIND_LEAF State
run_away_state, // on MOUSE_COURSOR_NEAR
find_leaf_state, // on MOUSE_COURSOR_DISTANT
go_home_state, // on LEAF_NEAR
no_change, // on ARRIVED_HOME
},
{ // RUN_AWAY State
no_change,
find_leaf_state,
no_change,
no_change,
},
{ // GO_HOME State
no_change,
no_change,
no_change,
find_leaf_state,
},
};
struct AntBrainState_t current_state = find_leaf_state;
for (;;)
{
current_state.stateFn();
enum ExternalEvent_e some_external_event = get_current_event();
struct AntBrainState_t next_state = transition_table[current_state.code][some_external_event];
if (next_state.code != NO_CHANGE)
{
current_state = next_state;
}
}
}
As you can see, transition tables offer a structured and concise way to represent state machines, making it easier to understand and modify the code in the future. Let’s see how this works in more detail.
The transition_table is a two-dimensional array of the AntBrainState_t struct, where the rows represent states and the columns represent external events. Each cell in the table contains the next state to transition to based on the current state and the external event.
For instance, Let’s take the first row which represents the FIND_LEAF state, and the first column which represents the MOUSE_CURSOR_NEAR event. In this case, the value of this element is run_away_state struct, which means that if the FSM is currently in the FIND_LEAF state and receives the MOUSE_CURSOR_NEAR event, it should transition to the RUN_AWAY state. The table follows the same pattern for all other state and event combinations. However, our implementation has a limitation when it comes to transitioning from the RUN_AWAY state to either the GO_HOME or FIND_LEAF state. For instance, if the FSM has transitioned from the GO_HOME state to the RUN_AWAY state and the MOUSE_CURSOR_DISTANT event occurs, it is expected that the FSM would transition back to the GO_HOME state. However, our implementation transitions back to the FIND_LEAF state instead. One possible solution is to use a stack to keep track of the previous states and allow for proper transitioning. However, the implementation of this solution is beyond the scope of this article. Instead, I’ll leave it as an exercise for the reader.
Conclusion
Transition tables are a concise solution for implementing finite state machines, but they can have some limitations with transitioning back to a previous state, as in the case of transitioning from the RUN_AWAY state to the GO_HOME state. One possible solution to this issue is to use a stack to keep track of previous states and transition back to them as needed.
That’s all for now.
Your encouragement and support mean a lot to me, so please consider following me or buying me a coffee at Ko-fi.com, it’s so appreciated!
Thanks for reading, and see you in the next one.
Level Up Coding
Thanks for being a part of our community! Before you go:
- 👏 Clap for the story and follow the author 👉
- 📰 View more content in the Level Up Coding publication
- 💰 Free coding interview course ⇒ View Course
- 🔔 Follow us: Twitter | LinkedIn | Newsletter
🚀👉 Join the Level Up talent collective and find an amazing job
Implementing Finite State Machines Using Transition Tables was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding - Medium and was authored by Mazin Awad
Mazin Awad | Sciencx (2023-06-01T13:37:54+00:00) Implementing Finite State Machines Using Transition Tables. Retrieved from https://www.scien.cx/2023/06/01/implementing-finite-state-machines-using-transition-tables/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
