This content originally appeared on HackerNoon and was authored by Phenomenology
:::info Author:
(1) Ahmed Farag Ali, Essex County College and Department of Physics, Faculty of Science, Benha University.
:::
Table of Links
Space-time quanta and Becken Universal bound
Space-time quanta and Spectral mass gap
Conclusion, Acknowledgments, and References
Abstract
Snyder’s quantum space-time which is Lorentz invariant is investigated. It is found that the quanta of space-time have a positive mass that is interpreted as a positive real mass gap of space-time. This mass gap is related to the minimal length of measurement which is provided by Snyder’s algebra. Several reasons to consider the space-time quanta as a 24-cell are discussed. Geometric reasons include its self-duality property and its 24 vertices that may represent the standard model of elementary particles. The 24-cell symmetry group is the Weyl/Coxeter group of the F4 group which was found recently to generate the gauge group of the standard model. It is found that 24-cell may provide a geometric interpretation of the mass generation, Avogadro number, color confinement, and the flatness of the observable universe. The phenomenology and consistency with measurements is discussed.
\ “The knowledge at which geometry aims is knowledge of the eternal”— Plato.
I. INTRODUCTION
In 1947, Snyder established a remarkable step that reconciles the minimal length of measurement with Lorentz symmetry by constructing quantum Lorentzian space-time [1]. The price was introducing non-commutative geometry and the generalized uncertainty principle (GUP) in Snyder’s algebra. For Non-commutative geometry part, it is found to emerge naturally at limits of M/string theory [2] as higher dimensional corrections of ordinary Yang-Mills theory [3]. Several implications of non-commutative geometry were investigated in quantum field theory and condensed matter systems [4, 5]. For the GUP part, it emerged in several approaches to quantum gravity such as string theory, loop quantum gravity, and quantum geometry [6–12]. Phenomenological and experimental implications of the GUP have been investigated in low and high-energy systems [13–25]. Useful reviews on quantum space-time and GUP can be found in [26–28]. Snyder’s algebra is generated by three main generators which are position xµ, momentum pµ and Lorentz generators Jµν = xµpν − xνpµ. They satisfy the Poincar´e commutation relations and suggest new commutation relations that provide a quantum/minimal length as follows:
\
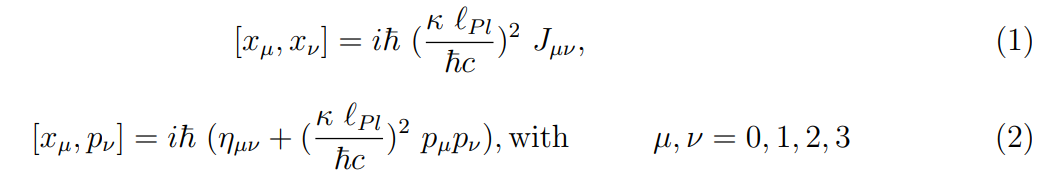
\ where ℓP l is a Planck length, κ is a dimensionless parameter that identifies the minimal measurable length, and ηµν = (−1, 1, 1, 1). Eq. (1) introduces the non-commutative geometry and Eq. (2) introduces a GUP. Both equations are invariant under Lorentz symmetry [1].
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Phenomenology
Phenomenology | Sciencx (2024-07-31T15:10:48+00:00) The Mass Gap of the Space-time and its Shape. Retrieved from https://www.scien.cx/2024/07/31/the-mass-gap-of-the-space-time-and-its-shape/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
