This content originally appeared on HackerNoon and was authored by The FewShot Prompting Publication
:::info Authors:
(1) Sebastian Dziadzio, University of Tübingen (sebastian.dziadzio@uni-tuebingen.de);
(2) Çagatay Yıldız, University of Tübingen;
(3) Gido M. van de Ven, KU Leuven;
(4) Tomasz Trzcinski, IDEAS NCBR, Warsaw University of Technology, Tooploox;
(5) Tinne Tuytelaars, KU Leuven;
(6) Matthias Bethge, University of Tübingen.
:::
Table of Links
2. Two problems with the current approach to class-incremental continual learning
3. Methods and 3.1. Infinite dSprites
4. Related work
4.1. Continual learning and 4.2. Benchmarking continual learning
5.1. Regularization methods and 5.2. Replay-based methods
5.4. One-shot generalization and 5.5. Open-set classification
Conclusion, Acknowledgments and References
5.3. Do we need equivariance?
By training a network to regress the value of each FoV, we learn a representation that is equivariant to affine transformations. However, we could also take advantage of the shape labels to learn an invariant representation that we could then use to perform classification. In this section, we directly compare equivariant and invariant learning to demonstrate further that learning an equivariant representation is the key to achieving effective continual learning within our framework.
\ Our baseline for invariant representation learning is based on SimCLR [5], a simple and effective contrastive learning algorithm that aims to learn representations invariant to data augmentations. To adapt SimCLR to our problem, we introduce two optimization objectives. The first objective pulls the representation of each training point towards the representation of its exemplar while repelling all other training points. The second objective encourages well-separated exemplar representations by pushing the representations of all exemplars in the current task away from each other. We observed that the first training objective alone is sufficient, but including the second loss term speeds up training. For each task, we train the baseline until convergence. At test time, the class labels are assigned through nearest neighbor
\
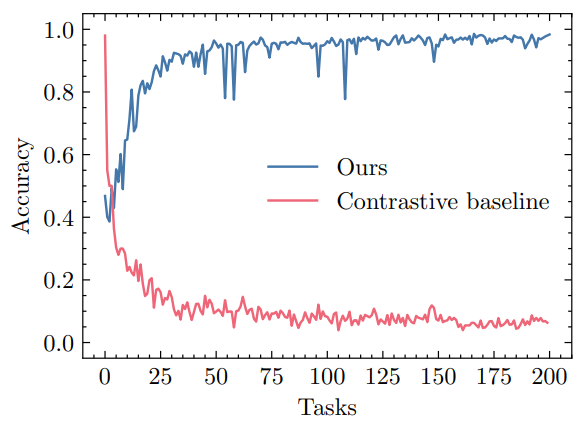
\ lookup in the representation space. Similar to our method, we store a single exemplar per class.
\ Figure 6 shows test accuracy for both methods over time. The performance of the contrastive learning baseline decays over time, but not as rapidly as naive fine-tuning. Note that in contrast to our method, invariant learning could benefit from storing more than one exemplars per class. The supplementary material provides an exact formulation of the contrastive objective and implementation details.
\
:::info This paper is available on arxiv under CC 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by The FewShot Prompting Publication
The FewShot Prompting Publication | Sciencx (2024-08-27T23:00:11+00:00) Why Equivariance Outperforms Invariant Learning in Continual Learning Tasks. Retrieved from https://www.scien.cx/2024/08/27/why-equivariance-outperforms-invariant-learning-in-continual-learning-tasks/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
