This content originally appeared on HackerNoon and was authored by Economic Hedging Technology
Table of Links
1.2 Asymptotic Notation (Big O)
1.5 Monte Carlo Simulation and Variance Reduction Techniques
- Literature Review
- Methodology
3.2 Theorems and Model Discussion
3. METHODOLOGY
3.1 MODEL ASSUMPTION
Let us consider a set containing n number of securities 𝑋𝑖 , 𝑖 = 1,2,3, … , 𝑛 which follows the multivariate continuous time
\
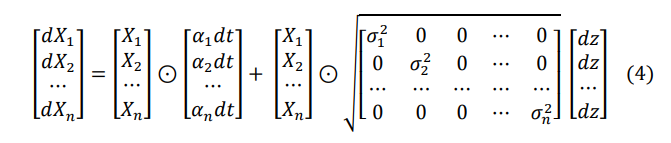
\ In a generalized way, we can write equation (4) as
\

\ With 𝜑 = (𝜑1 ,𝜑2 , … ,𝜑𝑛)′. We are able to identify in closed form the trade-off between hedging idiosyncratic versus systematic option risk at the portfolio level by concentrating just on one systematic risk element. Now we can rewrite (5) for the ith security as
\
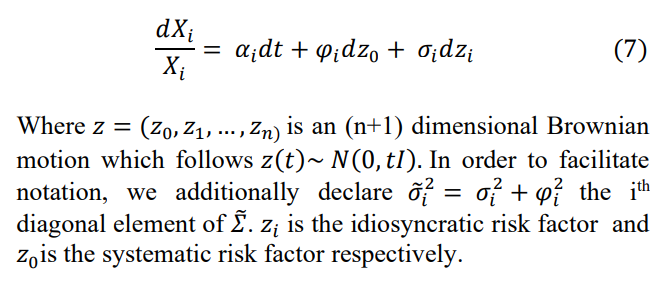
\ However, the normal Black-Scholes hedge is no longer perfect in discrete time; that is, the expected return of the hedge portfolio no longer vanishes nearly absolutely but merely in expectation. In this study, we demonstrate that a smaller hedge error variance in discrete time can be obtained with various hedge portfolios [17]. Instead of concentrating on the linear exposure to overall risk, that is, systematic plus idiosyncratic risk, these alternative hedge portfolios highlight the higher-order exposure to the systematic risk element.
\ Let us discuss another mathematical assumption based on Finite difference concept [18]. Finite difference methods approximate derivatives of functions by expressing them as weighted combinations of function values at nearby points. One way to derive finite difference formulas is through Taylor series expansion.
\ Consider a function 𝑓(𝑥) that is sufficiently smooth, such that it has continuous derivatives up to some order in a neighborhood of a point 𝑥 [19]. The Taylor series expansion of 𝑓(𝑥) about 𝑥 is:
\
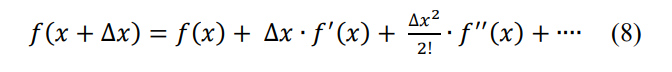
\ Now, let's focus on approximating the first derivative 𝑓′(𝑥). Subtracting 𝑓(𝑥) from both sides of the Taylor series expansion gives:
\
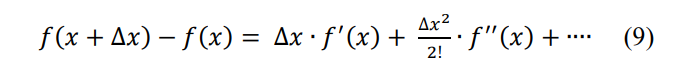
\ If we solve this equation (9) for 𝑓′(𝑥), we get:
\
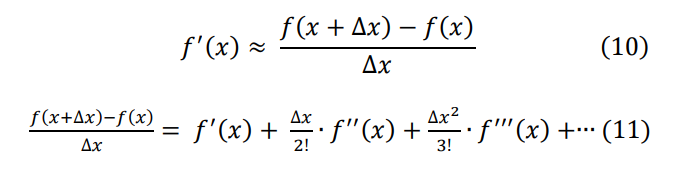
\ From the concept of asymptotic notation, we can write equation (11) as:
\
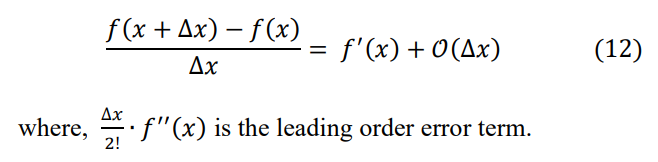
\ This is a finite difference approximation for the first derivative of 𝑓(𝑥). The error decreases as Δ𝑥 decreases, with higher-order terms becoming relatively less significant.
\ Similarly, higher-order derivatives can be approximated using finite differences derived from Taylor series expansions [20]. These finite difference formulas provide a way to numerically approximate derivatives of functions, which is fundamental in many areas of applied mathematics and computational science [21].
\
:::info Authors:
(1) Agni Rakshit, Department of Mathematics, National Institute of Technology, Durgapur, Durgapur, India (spiritualagnimath.statml@gmail.com);
(2) Gautam Bandyopadhyay, Department of Management Studies, National Institute of Technology, Durgapur, Durgapur, India (gbandyopadhyay.dms@nitdgp.ac.in);
(3) Tanujit Chakraborty, Department of Science and Engineering & Sorbonne Center for AI, Sorbonne University, Abu Dhabi, United Arab Emirates (tanujit.chakraborty@sorbonne.ae).
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Economic Hedging Technology
Economic Hedging Technology | Sciencx (2024-10-23T06:23:02+00:00) Enhancing Hedge Error Approximations in the Black-Scholes Model. Retrieved from https://www.scien.cx/2024/10/23/enhancing-hedge-error-approximations-in-the-black-scholes-model/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
